谱配置点法和Lobatto IIIA方法求解一维热传导方程

王佩臣，宋玉琦，郭巧栋，张可为，田国华

（1.黑龙江工程学院 数学系，黑龙江 哈尔滨150050；2.哈尔滨医科大学，黑龙江 哈尔滨150001）

1 方程简介

考虑下面热传导方程的初边值问题：

其中：ψ1（t）、ψ2（t）、f u，x，（）t和φ（）x为已知函数。

热传导方程的解具有将初始温度平滑化的特质，描述热从高温处向低温处传播，求解热传导方程是一个很重要的任务。对热传导方程通常用分离变量法［1］求得精确解；文献［2］用半离散差分格式数值求解一维热传导方程；本文组合谱配置点法［3－5］和 Lobatto IIIA 方 法［6－9］求 解 一 维 热 传 导 方程，具有计算精度高和稳定性好等特点。

2 谱配置点法及微分矩阵

以xi为节点的Lagrange插值多项式为

这里D＝（Dkm）为（N＋1）×（N＋1）矩阵，进一步，再对pN（x）求二阶导数，得

3 Lobatto IIIA方法

考虑下面初值问题：

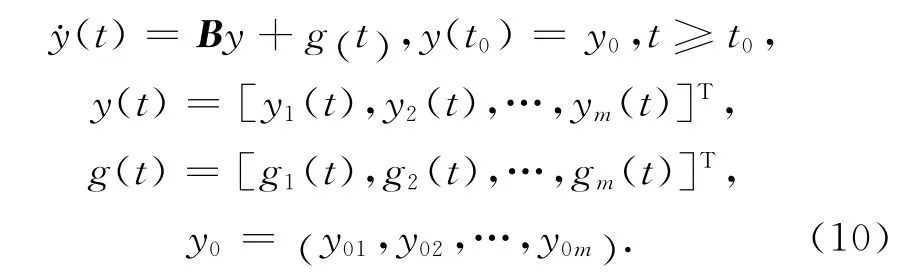
其中B是m×m矩阵，m为正整数。

本文使用下面迭代过程

系数用下面Butcher’s矩阵表示

对式（11）第二个式子移项得

HK＝b，解这个方程组就能得到向量ki，i＝1，2，…，q，进一步可循环求解yn＋1，用递推的方式就能得到式（10）的解。本文的数值计算取文献［6］中的Butcher’s矩阵，q＝4，如下

4 谱配置点法求解一维热传导方程

方程（1）在x＝xk，k＝1，…，N－1精确表示为

由第1部分谱配置点法可得式（13）等价于

使用第2部分的Lobatto IIIA方法求解边界条件（16）的常微分方程（15）就能得出原方程的解。

5 数值实例

初始条件为

图1为方程（17）在t＝1时精确解曲线图，图2为方程（17）取h＝0.01、N＝10、t＝1时的数值解曲线图，图3为方程（17）取h＝0.01、N＝10、t＝1时的误差曲线图。

6 结束语

本文组合使用配点法和六阶Lobatto IIIA方法求解一维热传导方程，首先使用配点法离散空间导数，然后用六阶Lobatto IIIA方法求线性解常微分方程组，通过数值测试实例，说明提出的方法有很高的精度和强稳定性，还可以用这个方法求解其他时间依赖问题。

［1］姜礼尚，陈亚浙，刘西垣，等.数学物理方程讲义［M］.北京：高等教育出版社，2003.

［2］李向正，张卫国，源三领.LS解法和Fisher方程行波系统的定性分析［J］.物理学报，2010，59（2）：744－749.

［3］Shen J，Tang T.Spectral and high－order methods with applications［M］.Beijing：Science Press，2006.

［4］Guo B Y.Spectral methods and their applications［M］.Hong Kong：World Scientific，1998.

［5］Canuto C，Hussaini M Y，Quarteroni A，et al.Spectral methods in fluid dynamics［M］.Berlin：Springer－Verlag，1987.

［6］Lambert J D.Numerical Methods For Ordinary Differential Systems The Initial Value Problem［M］.New York：John Wiley ＆Sons.

［7］Butcher，J C.The Numerical Analysis of Ordinary Differential Equations：Runge－Kutta Methods［M］.Wiley，New York，1987.

［8］K Dekker，Verwer，J G.Stability of Runge-Kutta Methods for Stiff Nonlinear Differential Equations［M］.North－Holland，Amsterdam，1984.

［9］E Hairer，S P.Nett，G Wanner.Solving Ordinary Differential Equations II，Stiff and Differential Algebraic Problems［M］.Springer，New York，2003.