基于遗传算法的自动组卷技术

2013-08-13杨巍巍宋海峰高巍巍马宪敏张丽明

黑龙江工程学院学报 2013年2期

杨巍巍，宋海峰，高巍巍，马宪敏，李放，张丽明

（1.黑龙江外国语学院，黑龙江哈尔滨150025；2.黑龙江工程学院，黑龙江哈尔滨150050；3.吉林华侨外国语学院，吉林长春130117）

自动组卷是依据用户指定的约束条件（查询参数）抽取出符合要求的试题并组合成试卷。组卷模块是整个网络考试系统设计中重要的组成部分。遗传算法（Genetic Algorithm，GA）是由生物进化论中的“适者生存，优胜劣汰”进化规律和遗传机制演化来的一类随机搜索方法。遗传算法借用生物遗传学的观点，通过自然选择、交叉、变异等作用机制，实现个体适应性的提高，从而体现了自然界中“物竞天择、适者生存”的进化过程［1］。

1 智能组卷技术

1.1 试题库结构

在数据库设计中，为单个试题设置题号、知识点、题型、预计用时、分值、难度、区分度、最近被选时间等多个属性描述［2］，以便于组卷时对整份试卷进行条件约束。

1.2 建立组卷数学模型

将自动组卷生成的试题，量化为包含题号、知识点、题型、答题时间、分值、难度和区分度等属性的一个n维向量（a1，a2，…，an），假设1份试卷中包含m道试题，则将生成的试卷表示为m×n的目标矩阵S［3］。

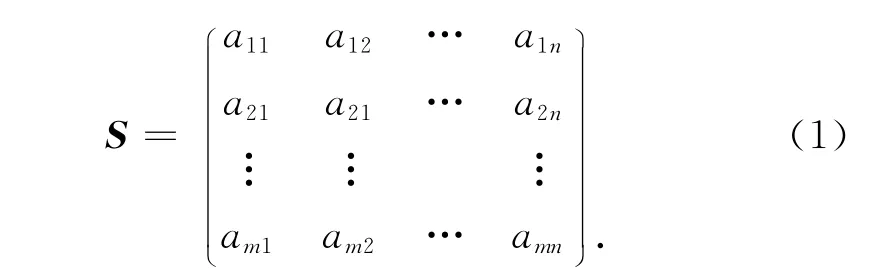
目标矩阵S主要满足以下约束条件［4］：

1）知识点约束。

式中：ZF 为试卷总分，zk（k＝1，2，…，n）为第k个知识点的总分，zpk为第k个知识点的分值占整个试卷的分值比例。

2）试卷题型约束。

式中：tk（k＝1，2，…，n）为第k种题型的总分值，tpk为第k种题型占整个试卷的分值比例。

3）试卷答题总时间。

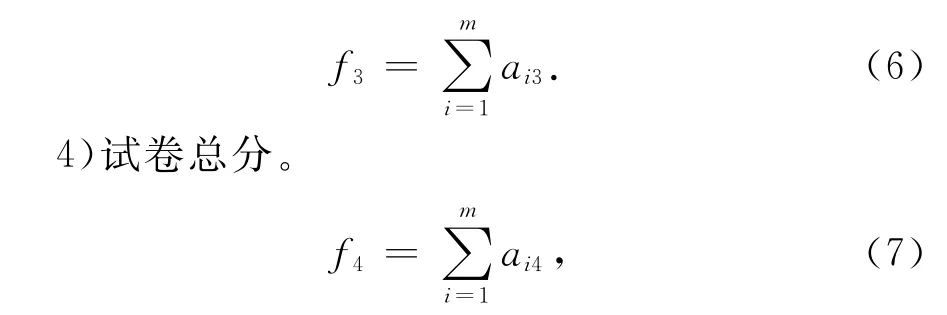
式中：f4为试卷题型分布指标中的ZF。

5）难度系数。

式中：wi为该试题的权值，较简单的题型权值比重分配较小，较难的题型权值比重分配较大。难度划分为5个等级：易［0.0～0.2）、较易［0.2～0.4）、中等［0.4～0.6）、较难［0.6～0.8）、难［0.8～1.0），默认值为0.6，也可由用户自行指定。难度系数越小，试卷越简单。

6）试卷区分度。

区分度值一般在－1～＋1之间，值越大区分度越好，说明试题设计得也越好。

2 遗传算法的改进及应用

2.1 染色体编码

将1份试卷映射成1个染色体，其中的各试题映射成基因，按照题型与知识点排序，生成试卷。在1份试卷中，染色体包含的编码个数即为试卷中试题的个数。将染色体表示为一维向量：（G1，G2，G3，…，Gn），其中Gi（i＝1，…，n，n为试卷中包含的总题目数）为试题的编号［5］。

传统的使用二进制编码存在搜索空间过大和编码长度过长等缺点，本系统中采用整数编码策略［6－7］，试题的每个属性值用整数来表示，如表1所示。

表1 试题编码

2.2 产生初始种群

根据预先设定的条件随机生成初始种群，种群规模需要根据实际情况来确定，一般来说在30～80之间较好。

2.3 适应度函数的设置

适应度函数在遗传算法中决定着个体的优胜劣汰，是群体进化的驱动力。在生成初始种群时，已对试卷总分数、总时间、所含题型和所含知识点进行约束，在设计适应度函数时，使用试卷的难度、题型分布和知识点分布的误差进行衡量。为了避免误差正负值之间互相抵消，使用误差的绝对值进行计算。设ei为第i个指标与用户要求之间误差的绝对值，wi为第i个指标对组卷重要程度的权值，设适应度函数f＝，当f的值达到最小时，组卷成功［4］。

2.4 遗传算子的改进

1）选择算子。采用按适应值排序择优的方法选择个体是被复制到下一代还是被淘汰。具体做法是：在父代中，对个体按照适应值排序，然后按照一定的概率来选择，将适应度高的部分个体遗传到下一代，其余部分个体或者进行交叉，或者进行变异。通过对算法进行试验，将适应度高的30%个体复制到下一代，形成子代种群。

2）交叉算子。交叉有单点交叉、双点交叉和多点交叉等，它使得群体形态多样化。因为初始种群已经按设定的组卷条件产生，因此，本系统采用单点交叉。在群体中，将个体按适应度值进行排序，选择适应度低的个体，两两配对，并在同一题型内，随机产生交叉位置，按照交叉概率Pc进行单点交叉操作，生成两个新的个体，如图1所示［9］。如果知识点重复，则重新产生交叉位置。将产生的新的个体适应度与群体中其他个体适应度进行比较，若适应度值高于其他个体中适应度最小的，则保留。对最终产生的新的种群，再按个体适应度值进行排序，适应度高的复制到子代。

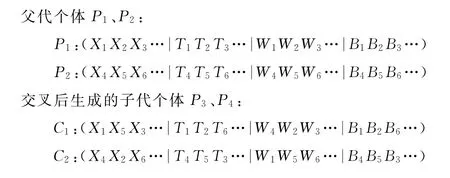
图1 单点交叉操作

图1 中，Xi表示选择题，Ti表示填空题，Wi表示问答题，Bi表示编程题。

3）变异算子。当两个个体相似度很高时，采用交叉操作很难产生新个体，采用变异操作可以抑制早熟。变异概率Pm值大，搜索范围大，群体多样性好，可以较好地抑制早熟，避免产生局部最优解；但Pm值太大，会失去从父代继承的优良个体，并导致算法收敛速度慢［10］。本文采用自适应函数动态调整交叉概率Pc和变异概率Pm，当种群中个体的适应度差别较大时，增大Pc的值，减小Pm的值，加快进化速度；反之，减小Pc的值，增大Pm的值，本文采用基本位变异算子，在个体中选择任意的位置进行基因的变异操作。