重力向下延拓计算分析

刘 涛，余志奇，王建强

（1.武汉市政设计研究院有限责任公司，湖北 武汉430079；2.东华理工大学 测绘工程学院，江西 南昌330013）

随着全球定位系统（GPS）定位精度的提高、惯性导航系统（INS）和重力测量系统的改进，航空重力测量在5～10km的空间分辨率尺度上能够达到1～3mGal（1mGal＝10－5m／s2）的数据精度，所提供的重力场中、短波信息与地面重力测量和卫星重力测量形成有效互补，特别是在地面重力测量难以达到的地区（如两极、森林和山区等），航空重力测量更是无可替代。航空重力测量观测值经过数据预处理，可得到飞行高度处的重力异常或重力扰动，但大地测量领域需要的是大地水准面上的重力值，因此，需将飞行高度处的重力异常或重力扰动向下调和延拓至大地水准面上。航空重力向下延拓是一个数据噪声放大的过程，属于病态问题，若不采用合适的延拓方法，将无法得到稳定可靠的重力延拓解。向下延拓的方法有多种，包括最小二乘配置［1］（LSC）、快速傅里叶变换［2］（FFT）、直接代表法［3］和求解球内 Dirichlet问题的直接法［4］。Poisson积分［5－8］法应用最为广泛。本文将对Poission积分方法进行研究，通过积分迭代计算过程实现重力向下延拓。作为对比分析，模拟区域选择在高山区域和平原区域，通过数据模拟得出该方法的延拓性质。

1 Poission积分

由于现代观测技术的发展，重力数据多种多样，但有时需要获取特定位置的重力数据，这时需要对重力进行延拓，对于重力延拓的研究，可参考文献［5］、［9］。假定在Bjerhammar球面上有连续分布的重力异常，以Bjerhammar球面为边界的第三边值问题基础上，重力延拓的计算公式［10］

式（1）的解目前还没有Poisson逆算子的封闭公式，可采用迭代法或将这一积分方程离散化，近似转化成一个线性方程组求解。以迭代法作为试验，式（1）可改写为

式中：P为计算点，Q′为σ面上的积分面元流动点，DPQ′＝lPQ′／rp。利用直接积分法可得

式（4）即为求解Δg＊P′的迭代计算公式，取初始值

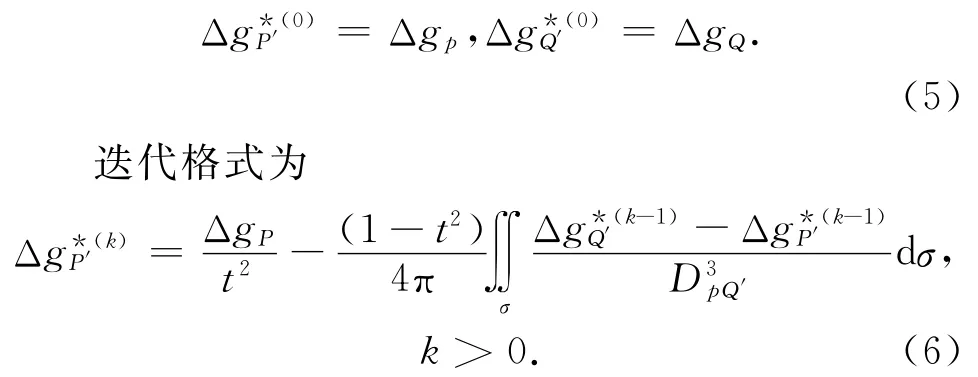
2 模拟计算

为了顾及地形对重力向下延拓的影响，试验计算了2个地区的重力延拓，区域位置同重力归算中的2个区域相同，分别为A区和B区，其中A区地势复杂，位于高山区域，B区地势平坦，位于平原区域。两个区域均为4°×4°的方块区域，计算结果如图1、图2所示，图中的（a）图为地面重力值，（b）图为向下延拓值。从图中可以看出，A区的重力异常比B区的重力异常范围要大，原因是A区的地形海拔落差比B区大。2个区域的延拓迭代计算统计如表1所示，要达到限差要求，A区需要迭代计算13次，B区迭代计算7次。

表1 迭代计算统计

3 结束语

利用Poisson积分进行重力向下延拓需要迭代计算，迭代计算的次数同地形有关。地形复杂区域重力异常波动范围大，重力向下延拓在保证相同精度下需要迭代的次数远大于平坦区域。模拟实验表明，地面观测数据向下延拓至椭球面上，由于距离较小，数值变化不大。由于重力向下延拓是一个误差放大的过程，因此，有必要对重力向下延拓的误差特性进行分析。

［1］FORSBERG R，KENYON S.，Evaluation and Downward Continuation of Airborne Gravity Data—the Greenland Example，in Proc Int Symp Kinematic Systems in Geodesy，Geomatics and Navigation［J］.Banff：［s.n.］，1994：531－538.

［2］C HWANG，HSIAO Y，SHIH H，et al，Geodetic and Geophysical Results from a Taiwan Airborne Gravity Survey：Data Reduction and Accuracy Assessment［J］.Journal of Geophysical Research，2007，112（B4）：1－14.

［3］Pan SHI，WANG Xingtao，The Frequence Domain Analysis for the Determination of Terrestrial Mean Gravity Anomaly Using Airborne Gravimetry［J］.Acta Geodaetica et Cartographica Sinica，1995，24（4）：301－308.

［4］Pan SHI，SUN Zhongmiao，The Solution to the Problem of the Spherical Interior Dirichlet and Its Application［J］.1999，3：195－198.

［5］MARTINEC Z.，Stability Investigations of a Discrete Downward Continuation Problem for Geoid Determination in the Canadian Rocky Mountains［J］.Journal of Geodesy，1996，70（11）：805－828.

［6］KERN M.，An Analysis of the Combination and Downward Continuation of Satellite，Airborne and Terrestrial Gravity Data［M］.Calgary：Universiy of Calgary，2003.

［7］Xingtao WANG，SHI Pan，ZHU Feizhou，Regularization Methods and Spectral Decomposition for the Downward Continuation of Airborne Gravity Data［J］.Acta Geodaetica et Cartographica Sinica，2004，33（1）：33－38.

［8］Jiang Tao，LI Jiancheng，WANG Zhengtao，ZHANG Shoujian，Solution of Ill－posed Problem in Downward Continuation of Airborne Gravit［J］.Acta Geodaetica et Cartographica Sinica，2011，40（6）：684－689.

［9］Hwang C.，Y.Hsiao，H.Shih，M.Yang，K.Chen，R.Forsberg，A.Olesen，Geodetic and geophysical results from a Taiwan airborne gravity sur－vey：Data reduction and accuracy assessment［J］.Journal of Geophysical Ressarch，2007，112 （B04407）：doi：10.1029／2005JB004220.

［10］李建成，陈俊勇，宁津生，等.地球重力场逼近理论与中国2000似大地水准面的确定［M］.武汉：武汉大学出版社，2003.