物理课堂教学中大学生思维能力培养刍议:以静电场中高斯定理的应用为例

王 勇，林智群，任文辉

(湖南农业大学 理学院，湖南 长沙 410128)

物理学作为自然科学和现代工程技术的基础，已被越来越广泛地应用到各门科学中。大学物理作为一门科学素质课，它对于培养学生科学的思维方法、创新能力、理论联系实际能力，以及树立学生科学的自然观、宇宙观和辩证唯物主义世界观等，有着其他课程所不能替代的作用。[1]在讲授物理定理的应用过程中，教师首先要引导学生描述、分析物理过程和物理规律，诱导学生讨论、提出问题，引导他们去分析问题，探究解决问题的关键点，从而启发学生主动地提出方案、方法去解决问题。这不仅是大学物理教学的理念模式，也是开设大学物理课程的动因。对此，笔者拟以静电场中高斯定理的应用讲授为例浅谈大学物理课堂教学过程中学生思维能力的培养。

1.引入静电场应用事例激发学生的热情和启发学生思考

日常生活、生产、工程应用静电场力的情况非常普遍，笔者在讲授静电场中高斯定理的应用前先通过引入静电场应用事例激发学生的学习热情。这些事例如：喷墨打印机应用平行板带电体激发的电场对运动的微小带电墨滴施加电场力的作用，从而使墨滴打印在特定的位置；静电火箭发动机应用静电场对带电离子进行加速得到高速运动的离子，高速运动的离子从火箭中喷射出来使火箭获得推力，利用这种微小推力可以使火箭保持飞行轨道、飞行姿态、箭星分离对接。这些特殊形状的带电体所激发的静电场强度分布情况决定了他们的应用范围和效果，所以求其电场强度非常重要，虽然学生利用已学过的场强叠加原理直接求解其电场强度是可行的，但是如应用高斯定理来求解特殊形状带电体所激发的电场强度相对简单得多。

高斯定理的数学表达式为：

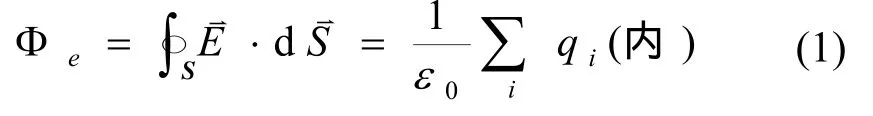
该式反映了静电场强度E在闭合曲面S的电通量，即在真空中静电场中通过任一闭合曲面S的电通量在数值上等于闭合曲面S所包围的电荷代数和的ε0分之一。[2]如果要用该式来求解电场强度，显然必须要能把E从积分号里面提取出来。为此，笔者引导学生思考：在什么条件下怎样才能将电场强度E从积分号里提取出来呢？是不是当E在被积区域闭合曲面S上处处大小相等是一个不变的常量时，才能把E当作常量从积分号里提取出来呢？接着，笔者引导学生深入思考电场强度E的矢量性。E是矢量不但有大小而且还有方向，所以还要求在闭合曲面S上E方向和面积元dS的法线方向一致。笔者待学生讨论之后，进一步启发学生总结分析结论，即要应用高斯定理求电场强度，最简单的一种情况是：找到一个闭合曲面S，电场强度E在这个闭合曲面S上处处大小相等、方向与曲面法线方向一致平行，即合适的高斯面。

接下来笔者启发学生分析场强与曲面的关系，引导学生思考如何建立高斯面。首先，笔者诱发学生思考问题：怎样去找，怎样去建立一个合适的闭合曲面呢？引导学生探究思考电场强度E，分析这个未知的电场，哪些点的电场强度大小相等，汇合成一个怎样的曲面，电场强度E的方向与什么样的曲面S平行、垂直。启发学生总结解决问题的方法，即要分析电场强度E分布特点：大小相等的点汇合成怎样的曲面，电场强度E方向与什么样的曲面平行、与什么样的曲面垂直。

2.以实例引导学生分析求解问题

为了更好地以实例引导学生分析求解问题，笔者以“求解无限大均匀带电平面的场强”为例进行了讲解。

(1)引导学生分析电场的分布特点(平面对称性)

笔者首先分析空间任一点P点的场强，它到平面的距离为r(图1)。

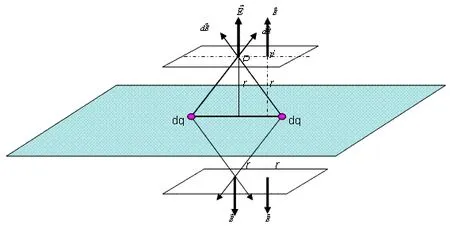
图1 带电平面的场强分析

在平面一直线上取一对对称的电荷元dq，它们在P点激发的场强大小相等，方向不相同，但叠加矢量之和后方向为垂直于无限大均匀带电平面向上，整个带电平面可看作无穷多对这样对称的电荷元组成，显然每一对对称的电荷元dq在P点所激发的场强矢量之和方向必垂直平面竖直向上的，所以P点的电场强度的方向为垂直于带电平面竖直向上。至此，笔者设问诱导学生思考“其他点的电场强度怎样？”显然其他点的电场强度可由P点的分析类似得来，即把P点的电场强度分析图平移。笔者进一步激发学生思考“这个平移过程意味着什么？是不是意味着只要这个点到平面的距离等于r，那么它的场强就与P点的场强相同？”接下来，笔者抛出问题激发学生思考“那么这些点汇合成一个怎样的曲面呢？”汇合成一个平行于带电平面的平面，即在这个平行平面上任一点的场强大小相等，方向相同垂直于平面向上。然后，笔者进一步激发学生探究带电平面下方的电场分布特点，通过PPT演示作图，引导学生思考得出结论：同样在相等距离r处，E大小相等方向相同垂直向下，即意味着下方场强大小相等的点同样汇合成一个等距平行平面，且场强的方向垂直向下。并且，笔者引导学生综合归纳电场强度分布特点：大小相等的点汇合成上、下等距平行平面，场强方向垂直平行平面，即具有面对称性。

(2)引导学生讨论怎样构建一个合适的闭合高斯面。因为高斯定理是指电场强度通过一个闭合曲面的电通量，为此，笔者引出解决问题的关键点：上、下两个平行平面还没构成一个闭合曲面，不能应用高斯定理求解，需要增加曲面与上、下两个平行平面拼合成一个闭合曲面。笔者激发学生思考“怎么找，找怎样的曲面呢？”“针对电场强度分布特点，考虑方向特点还有哪方面没分析？什么样的曲面与E电场强度平行？”诱导学生得出结论：只要与带电平面垂直的面都与电场强度E平行。然后，笔者进一步诱发学生思考“具体有什么形态的曲面？”笔者利用肢体动作形象地比划，左、右加垂直于带电平面的平行平面，前、后也加垂直于带电平面的平行平面，就构成了一个长方体。“这样是不是就构建了一个适合的闭合曲面了呢？就可以应用高斯定理了呢？试想还可作其它合适形式的高斯面吗？”通过连续发问，笔者促使学生发散思维、创造性地提出其他形状的合适的闭合曲面，比如可不可以作一个圆柱形，侧面垂直于带电平面。

(3)引导学生总结归纳解题和拓展思维。由分析可知，所得电场强度分布具有面对称性，可建立一个圆柱形高斯面(图2)：上、下底面等距平行于带电平面，侧面垂直于带电平面。

应用高斯定理：

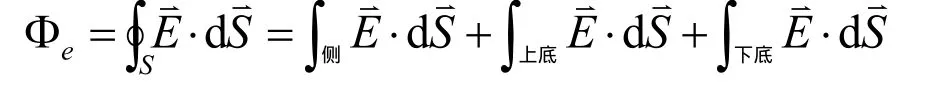
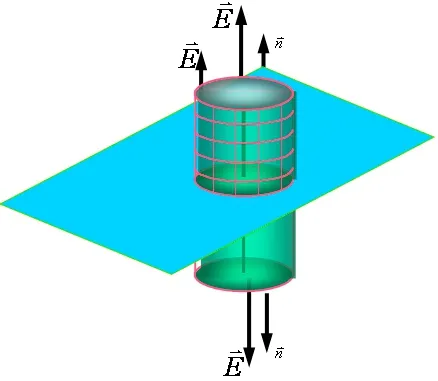
图2 圆柱形高斯面

笔者引导学生计算侧面的电通量。由于电场强度E与侧面处处dS方向垂直，cOSθ=0，故侧面的电通量为零。为使学生思考能顺利解决问题的关键点：侧面是我们加的曲面，从而才能构建一个闭合曲面(圆柱形)，才能应用高斯定理求解场强，然而它的电通量为零却没有给计算带来麻烦。笔者向学生提出问题“为什么要加这样的曲面？”诱导学生思考、回答问题。因为在分析电场强度E方向特点时，与场强平行、垂直的曲面都要分析，以便增加与场强平行的电通量为零的曲面构建一个合适的完全闭合曲面。

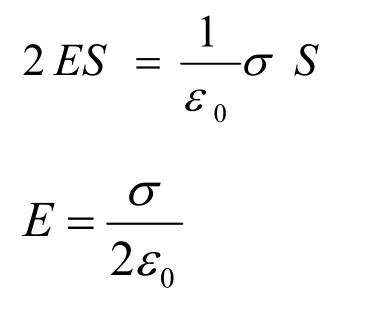
笔者引导学生分析讨论：电场强度E为常量，所以无限大均匀带电平面的电场是一个均匀电场，即电场强度处处大小相等、方向相同垂直带电平面向外。

最后，笔者向学生提出问题“由不考虑厚度的带电平面拓展到有一定厚度的带电平板的电场怎样求场强？”要求学生课后思考、讨论，以进一步激发学生分析问题、解决问题的欲望。

(4)总结解题步骤，引导学生理清思路，培养思维能力。一是分析电场的分布特点。应用取对称电荷元叠加法定性分析：1)电场强度E：大小相等的点汇合成怎样的曲面S1；2)电场强度E的方向特点：场强E与怎样的曲面S2平行，与怎样的曲面S3垂直。总结出该电场的对称性，如球对称性、面对称性、轴对称性等。二是联合曲面S1、S2、S3构建一个闭合曲面S，即合适的高斯面，从而应用高斯定理数学式可把E提到积分号之外。三是求出高斯定理数学式的右边闭合曲面所包围的电荷代数和，从而就可以求出电场强度的大小。

[1]韩红梅.论大学物理教学目的的应然和必然[J].中国教育导刊，2006(14)：41-42.

[2]吴百诗.大学物理基础[M].北京：科学出版社，2007.