一种快速FH－OFDM通信帧格式及其验证

孙宇明，赵 鹏，王 青，朱 倩

(北京控制工程研究所，北京 100190)

责任编辑:薛 京

跳频技术(Frequency－Hop，FH)是扩频通信技术的一种，它具有抗干扰和保密性强的优点。但是，它在多径信道下的通信能力不佳，且频谱利用率低。跳频速率的高低直接反应了跳频通信系统抗干扰能力的好坏，跳频速率越高，抗干扰性能越好［1－3］。正交频分复用(Orthogonal Frequency Division Multiplexing，OFDM)技术利用并行的正交载波并行传输数据，因为其符号持续时间长，所以对多径信道具有一定的适应能力［4－6］。特别是循环前缀的OFDM符号格式的引入，使得多径数目在其循环前缀长度范围内的信道对信号接收无影响。但是，OFDM具有对同步精度要求高的缺点［7－10］。跳频技术和OFDM技术结合的通信系统(FH－OFDM)，具有抗干扰、抗多径、频谱利用率高和保密的优点，在未来的认知无线电通信和保密通信中会得到广泛的应用。

对于一般的跳频通信系统，为了提高系统的抗干扰和保密性能，需要其跳频时间间隔足够短，对于FHOFDM系统来说其跳频时间间隔最小为1个数据符号。由于FH－OFDM发射机和接收机在切换频率时，都会有一定的频率和相位残差，这就需要在一个符号内快速实现OFDM信号同步的算法来解决这一问题。

文献［11］提出了基于循环前缀的算法，但是由于其定时算法具有平台效应，导致其小数倍频偏估计算法精度低。文献［12］提出基于训练序列的算法，虽然具有较高的同步精度，但是会降低跳频速率。文献［13－15］提出了使用时域隐含训练序列进行OFDM同步的算法，但会给接收信号带来无法弥补的噪声。

本文提出了一种隐含序列的FH－OFDM通信系统物理层帧格式，利用伪随机序列的相关特性，在一个OFDM符号内隐藏1个伪随机序列，利用其自相关特性对系统进行整数倍频率、定时同步和采样时钟同步。同时，增加了循环前缀长度以提高小数倍频偏估计精度。

1 系统模型

假设传输的数据为s(n)=sx(n)+sp1(n)，其中，sx(n)表示OFDM不添加训练序列的数据信号，sp1(n)表示伪随机基带信号的数据符号，即

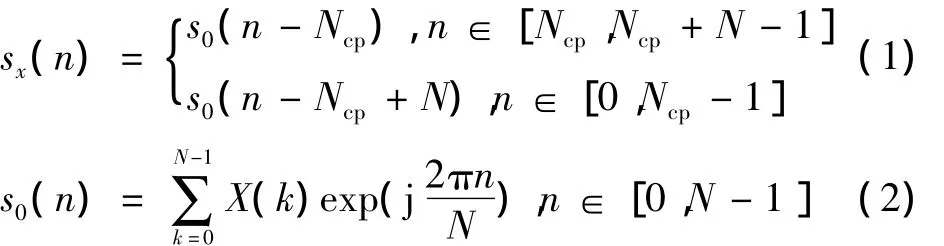
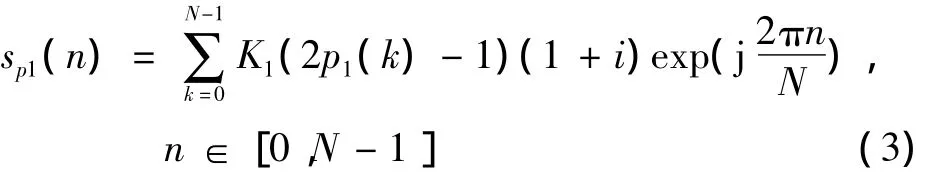
式中:X(k)表示各个载波上调制的数据;p1(n)表示伪随机序列;K1表示伪随机序列的幅度系数;Ncp表示循环前缀的长度;N表示一个OFDM符号传输的数据数目。

接收端收到的信号可以表示为

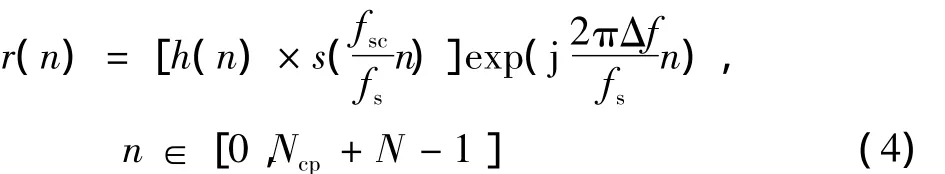
式中:h(n)表示通信信道引起的冲激响应;fsc表示发射端基带数据采样率;fs表示本地接收机的采样率;Δf表示接收信号的频率残差。在接收端的同步，就是在时间轴上估计出每个OFDM跳频符号起始点n=0的时刻、fs与fsc的比例关系和Δf的数值。

2 帧格式设计

根据扩频通信的基本原理，要检测到隐藏在OFDM符号中的训练序列，要求满足

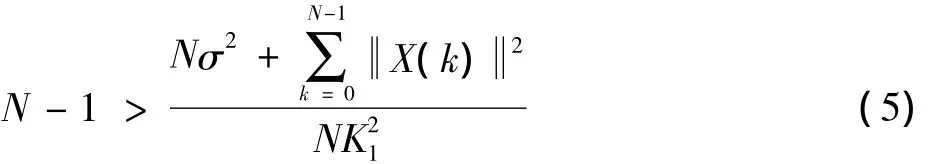
式中:σ2表示高斯白噪声的功率。

为了消除多径对于信号传输的影响，要求Ncp长度大于多径长度。同时，以插入梳状导频的方式来作为信道估计的依据，导频间隔大于通信信道的相干带宽。下面以设计一个带宽为10 MHz、跳频速率为2 kHz、最大多径时延为6.4 μs的系统为例设计一种帧格式。由带宽和跳频速率可知，每个频点上信号持续的时间为500 μs。

首先，设计OFDM符号。为了在设计中使用快速傅里叶变换算法，OFDM的载波数目可以设置为4 096，则其持续时间为409.6 μs，循环前缀长度需要大于等于最大时延，而且需要利用其冗余特性估计小数倍频率偏差，可以设其持续时间为32 μs，数据符号持续时间为441.6 μs，其他58.4 μs作为跳频系统的频率转换时间余量;设梳状导频的频率间隔为8;数据和导频符号采用QAM调制方式传输。

其次，设计扩频序列。对于长度为441.6 μs的数据符号，隐藏在其中的扩频序列可以选则长度为4 095的m序列，不妨设其生成多项式为(10123)8。其幅度能量为OFDM符号能量均值的1%，即其幅度为X(k)的10%。

最后，该系统的帧格式为

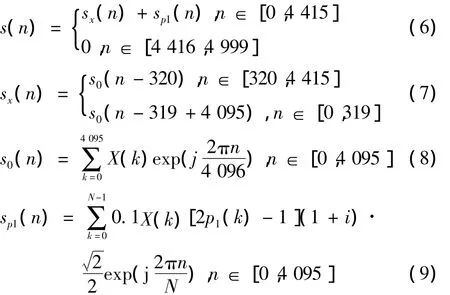
3 通信系统实现方法

3.1 发射机实现方法

发射机实现步骤如图1所示。信源模块将需要传输的数据发送至星座映射模块;星座模块按照星座要求对数据进行星座影射，本文的例子则采用4QAM调制方式，对于I路和Q路，1代表调制数据1，－1代表调制数据0，零频率上不调制数据。插入导频模块按照数据的顺序将星座映射后的数据分组，在其中间插入导频。对于本文为例的系统，其导频间隔为8，导频处均调制数据“11”，在0载波上不调制数据。训练符号生成模块按照系统的生成多项式生成扩频序列，对于本文的例子来说，扩频序列的生成多项式为(10123)8。IFFT模块对插入导频后得到的数据叠加训练序列后进行快速逆傅里叶变换，将数据符号调制到各个载波上。信号叠加模块将OFDM符号按照式(6)～(9)的要求留出58.4 μs作为跳频信号的时间转换余量。跳频控制模块按照事先给定的调频图案，控制上变频模块将信号发射出去。

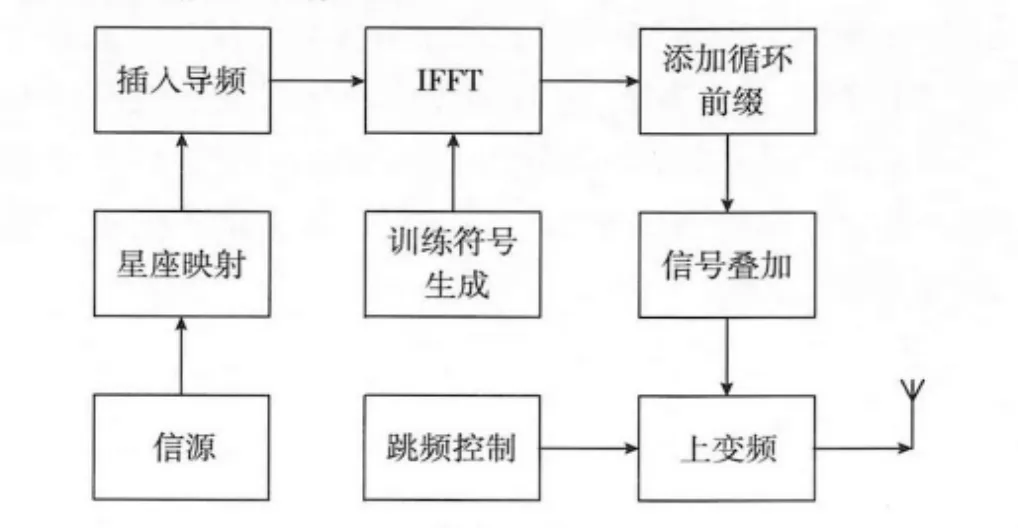
图1 发射机实现方法

3.2 接收机实现方法

接收机实现步骤如图2所示。

接收机在捕获状态，定时同步模块控制下变频模块在跳频图案的任意一个频点上等待，将射频信号变为中频信号。首先，采用缓存数据相关求能量的方式对接收信号进行检测，当检测结果大于检测门限时，认为捕获初步成功，控制下变频模块使下变频频率为跳频图案上的下一频点;然后，利用训练序列检测该符号，最大值是否过门限。门限计算结果为

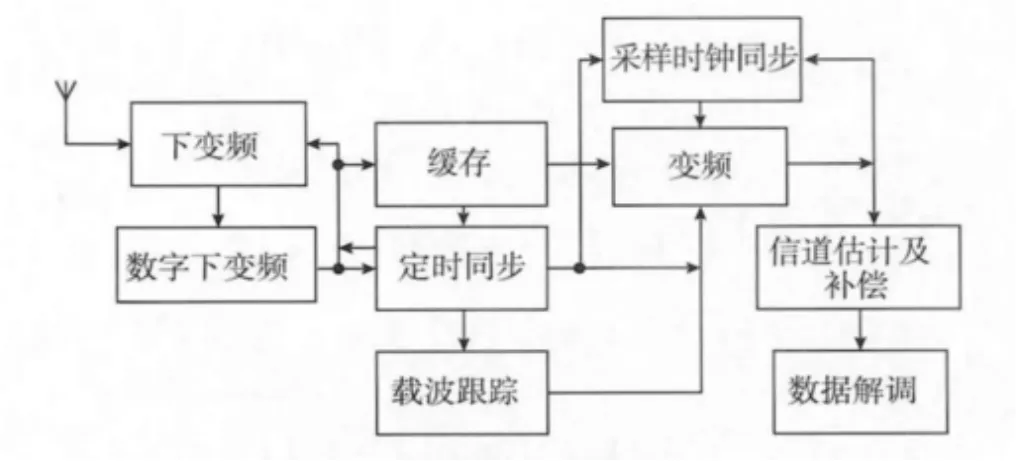
图2 接收机实现方法

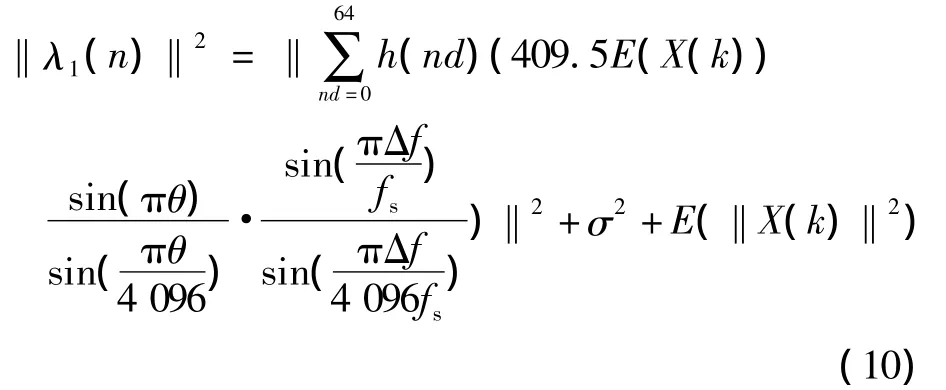
其中，当θ=0.5 ，Δf=0.5fs，信噪比为1 dB，最强劲能量为总能量的50%时，λ1(n)可以作为该系统训练序列的捕获门限。如果连续检测3个频点都过门限，则系统进入跟踪状态。否则，掉换训练序列的相位，再次进行训练序列检测。如果所有相位都没有过门限或者3次过门限则捕获失败，跳回起始频点。在捕获同时，缓存每一个采样值，缓存器的存储量=采样位数×采样率/信号带宽×5 000。接收机在跟踪状态时，一方面载波跟踪模块利用基于循环前缀的算法完成小数倍频偏估计，将小数倍频偏估计结果和定时同步模块估计出的整数倍频偏结果均输送给变频模块，变频模块整合两个频偏对缓存的数据进行数字下变频;另一方面，定时同步模块将训练序列的相关结果发送给采样时钟同步模块作为初始值，之后接收变频模块输出数据的训练序列检测结果作为鉴别器输入。鉴别器输出结果为

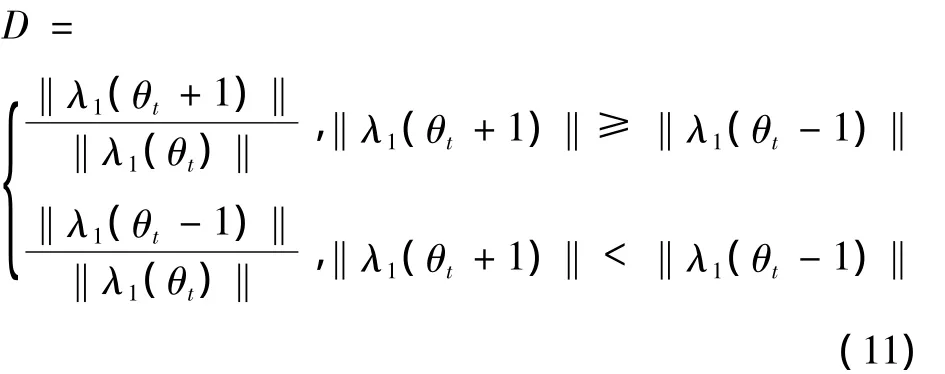
再经过二阶环路滤波后输出给变频模块。其中，可以直接从IFFT输出的检测结果取得最高和相邻次高点来作为鉴别器输入。变频模块内部使用全数字插值滤波器按照采样时钟同步模块输出结果对缓存后数据进行频率补偿，按照OFDM传输信号调制方式的不同可以选择不同的插值滤波器，对于QPSK调制方式的OFDM信号，使用线性插值滤波器即可。变频模块输出的数据作为解调结果，并对其进行信道估计。信道估计时，导频点采用LS算法+线性插值算法，且进行信道补偿，与输出数据进行复数除法并且减去训练序列，得到星座映射前的数据。数据解调模块完成星座图映射，从而完成数据解调。

4 仿真验证结果

仿真设置如下:跳频信号周期为64，在64个频点上切换，仿真中假设跳频信号顺序跳变，为了在MATLAB中体现跳频效果，特别设计两个跳频数组，存储64个频点的序号，只有当2个数组的序号完全吻合时，接收端才能获得发射端数据，带宽为10 MHz，基带数据传输率为14.324 Mbit/s，可以满足数字视频传输要求。下变频后的中频信号，其中心频率是从11～13 MHz间的随机数，以模仿真实信道中发射和接收设备间的随机频率差异。采样率是从40.004～39.996 MHz间的随机数，即4倍基带信号的采样率，再加上100×10－6的采样频率偏差，该输入信号的采样率偏差由插值滤波器实现。发射信号的调制方式为QAM，导频传输的数据为“11”。自载波个数为4 096，其中有效子载波个数为4 095，0频率上无数据。其他设置已经在第2节说明，不再赘述。接收机和发射机实现方法如第3节所述，信号经过多径长度为64个样值点、平均功率为指数的信道，多径样值点分别为0，3，5，7，9，63。传统基于CP的OFDM帧格式也可以由式(6)表示，此时sp1(n)=0。

在信噪比为1 dB、小数倍频偏为1 034 kHz时，伪随机序列依然能够被检测到而且十分尖锐，可见其能够精确定时，其定时精度在一个样值点之内。同时可以获得无符号间干扰的小数倍频率偏差估计样本空间。如图3所示，峰值点精确的在第321个样值点出现，定时的起始位置在一帧的开始，即符号定时位置相差320个样值点，与设置相同。与传统帧格式相比，观测值更尖锐，峰值点出现位置更精确。

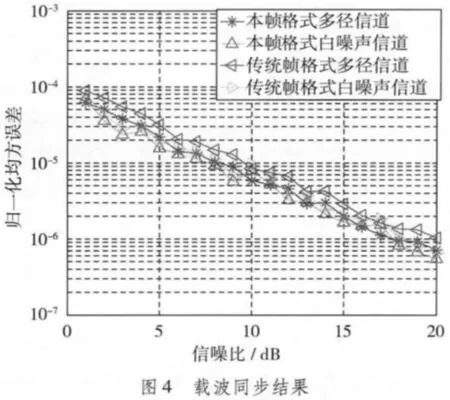
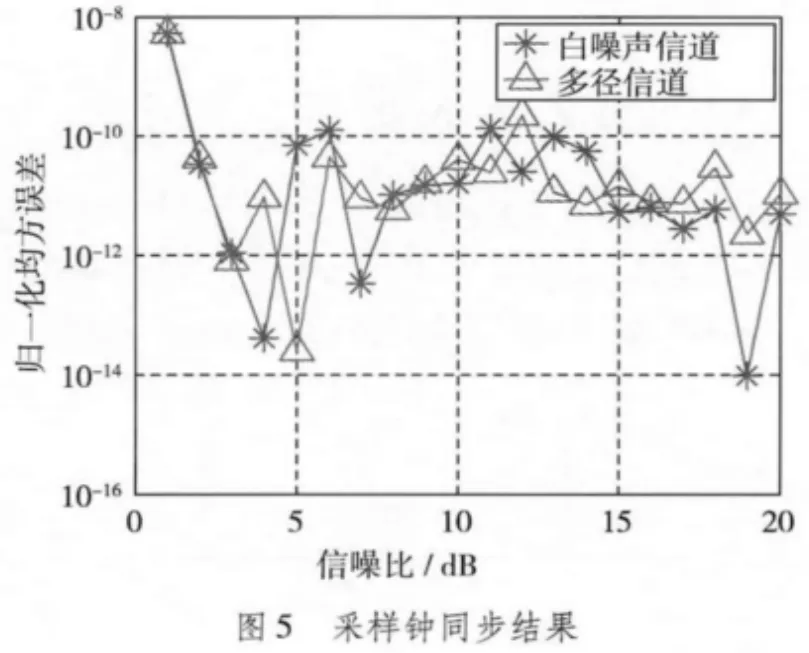
分别在多径和白噪声信道下，从1～20 dB，每隔1 dB仿真20 000个符号，统计载波同步偏差和采样时钟同步误差。如图4所示，本文帧格式载波同步的归一化均方误差在信号经过多径和高斯白噪声信道时相当，均小于10－4，引起的符号间干扰能量在工程上与噪声相比可以忽略，能够满足系统工作要求。与传统帧格式的均方误差相比较小。如图5所示，在信噪比大于3 dB时，采样时钟同步的归一化均方误差均小于10－10，引起的符号间干扰能量在工程上与噪声相比可以忽略，能够满足系统工作要求。而传统帧格式无法完成采样时钟同步，对发射和接收设备主时钟精度要求高。

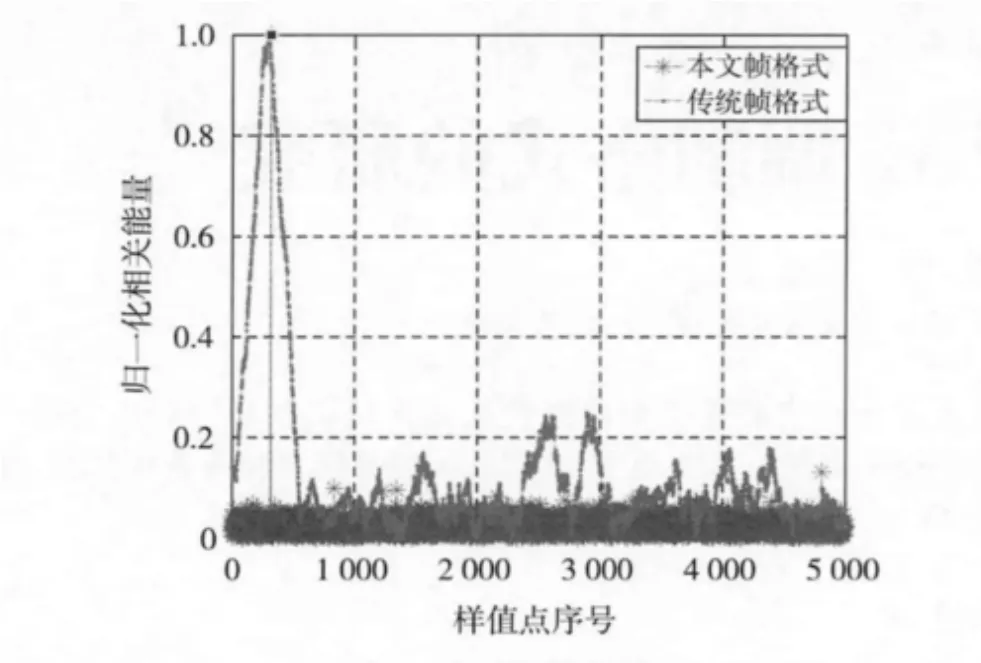
图3 定时同步峰值

使用Xilinx公司的XC4VLX40－10I的FPGA芯片实现本文所述的发射机，XC4VSX55－10I的FPGA芯片实现本文接收算法，通过AD9957实现跳频。在室内多径信道条件下，发射信号格式和接收算法与仿真相同。在约10 dB信噪比下，误码率小于10－8，使用线上逻辑分析仪Chipscope截取数据后绘制星座图，如图6所示，星座图能够很好收敛，说明该跳频OFDM通信系统可以很好地满足高数据率传输的要求。

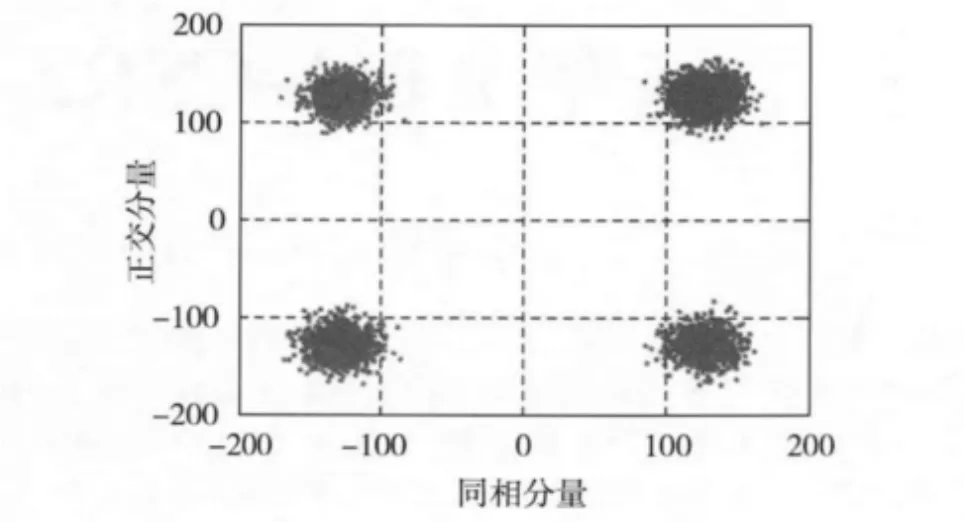
图6 实验星座图

5 结论

本文提出了一种快速跳频OFDM系统的实现方案，并以跳频速率为2 kHz、带宽为10 MHz的通信条件为例，设计了一个实际的FH－OFDM系统。该系统加入了较长的循环前缀，实现对于OFDM信号的快速载波精确同步;加入了信道补偿后可消除的频域训练序列，同时利用伪随机序列的相关性进行采样时钟同步，实现了精确的定时同步、采样时钟频偏估计和整数倍频偏估计;引入了梳状导频对多径信道进行估计。仿真结果表明，在白噪声和多径信道下，载波同步归一化均方误差均小于10－4，比传统帧格式的均方误差小，定时同步精度在一个样值点之内，与传统帧格式相比，观测值更尖锐，峰值点出现位置更精确;采样时钟同步归一化均方误差在信噪比大于3 dB情况下均小于10－10，而传统格式无法完成采样钟同步。实验结果表明，在约10 dB信噪比下，误码率在10－8以下，星座图能够很好收敛，能够满足未来的认知无线电通信和保密通信的应用要求。

［1］田日才.扩频通信［M］.北京:清华大学出版社，2009.

［2］魏鹏，李永超，陆锐敏.基于FPGA的π/4DQPSK跳频调制器的设计与实现［J］.电讯技术，2012，52(2):190－193.

［3］高军涛，胡予濮，李雪莲，等.两类最优跳频序列集的线性复杂度［J］.通信学报，2012，33(2):175－181.

［4］尹长川，罗涛，乐光新.多载波宽带无线通信技术［M］.北京:北京邮电大学出版社，2004.

［5］周围，刘燕容.基于叠加导频的MIMO－OFDM半盲信道估计［J］.电视技术，2013，37(3):9－14.

［6］崔丽珍，孙瑞璇.基于IEEE 802.11a的OFDM系统信道估计算法研究及实现［J］.电视技术，2012，36(5):97－100.

［7］崔丽珍，樊晓冬，刘乃君，等.基于FPGA的OFDM基带发送系统设计与实现［J］.电视技术，2012，36(21):11－15.

［8］FUSCO T，TANDA M.Blind synchronization for OFDM systems in multipath channels［J］.IEEE Trans.Wireless Communications，2009，8(3):1340－1348.

［9］KAI S，SERPEDIN E，CIBLAT P.Decision－directed fine synchronization in OFDM systems［J］.IEEE Trans.Communications，2005，53(3):408－412.

［10］熊兴中，骆忠强，郝黎宏.OFDM－IDMA系统的迭代频偏估计及补偿［J］.电讯技术，2012，52(10):1602－1607.

［11］SCHIMDL T，COX D.Robust frequency and timing synchronization for OFDM［J］.IEEE Trans.Communications，1997，45(12):1613－1621.

［12］GUO Y，LIU G，GE J.A novel time and frequency synchronization scheme for OFDM systems［J］.IEEE Trans.Consumer Electronics，2008，54(2):321－325.

［13］DAI Lingdong，WANG Zhaocheng，WANG Jun，et al.Joint time－frequency channel estimation for time domain synchronous OFDM systems［J］.IEEE Trans.Broadcast，2013，59(1):168－173.

［14］王平，袁伟娜，范平志.隐含训练序列信道估计中的功率分配［J］.电子与信息学报，2008(7):71－75.

［15］罗仁泽，戈勇华，党煜蒲，等.叠加弱能量序列的OFDM系统时频同步方法［J］.电子学报，2012，40(2):412－417.