基于改进C-V模型的图像分割算法
2013-08-13杨艳丹韩雪松韩应征庞冬冬杜军慧
杨艳丹,韩雪松,韩应征,庞冬冬,杜军慧
(1.太原理工大学信息工程学院,山西 太原 030024;2.中石化山西分公司,山西 太原 030024)
责任编辑:时 雯
为了使得数据形式能够适合计算机处理,在绝对大部分的图像分析中,必须把单个目标从图像中分离出来,形成目标与背景分离,这种处理方式即为图像分割,图像分割就是根据规定的准则把给定的图像分成具有不同特性的图像部分,图像分割的算法往往是根据规定的准则,图像内部灰度颜色纹理等特点目标与背景的不同来预先建立[1-2]。
在很多的图像分析应用的领域如遥感测量、医学成像、安全管制、军事目标检测都需要用到图像分割技术,图像分割技术越来越重要。在实际的图像分析应用中,当所需目标被分开时,分割就可以停止了,运用自动的图像分割算法去判别图像分割停止是很困难的[3]。况且在实际中,许多图像不是理想的图像,大部分图像是带有噪声的图像,且有些图像的灰度具有不均匀、分辨率差等缺点,这使得自动图像分割技术的实现遇到很多困难。近年来,主动轮廓模型在图像分割方面逐渐受到人们重视[4]。
随着主动轮廓模型的提出,使得在图像分割中得到的具有不同特性的子区域都有自己完整的边界,而现如今的各种算法,在处理图像时所得到的边界大部分都是断断续续的,很难形成一个完整的边界,所以这是使用主动轮廓模型最大的好处[5]。同时,在应用方面,由于与水平集理论的结合,主动轮廓模型的使用更加广泛。在许多分割方法中提到的常用的图像特性,如边界信息、区域统计信息和纹理信息都可以应用到主动轮廓中来[6]。
在主动轮廓模型中,最为经典的为Chan-Vese模型(以下简称C-V模型),C-V模型是一种基于区域的动态轮廓模型。C-V模型根据全局图像统计信息来完成对图像的分割。假设图像目标是由同质的区域构成,一般能得到良好的实验结果,但在实际情况中,图像的目标并非同质[7]。C-V模型在分割非同质目标时,得到的结果不是很理想;同时,在演化过程中,要不断地将水平集函数重新初始化,增加了迭代时间,使轮廓曲线演化速度大大降低。
1 Chan-Vese模型
在Chan和Vese Mumford-Shah分割模型的基础上提出了分段常量主动轮廓模型[7-8]。分段常量主动轮廓模型通过移动可演化的轮廓来最小化核心函数寻找目标边缘。在整个图像区域中,应用灰度统计信息来表示分段常量。通过比较在每一个像素点处的分段常量和真实图像的灰度区别就是核心函数的主要工作。
C-V模型是简化版的M-S模型。C-V模型的检测边界原理是不通过图像中的梯度信息来进行计算。在定义图像域Ω中,进行演化的边界C属于Ω中一个子集ω的边界,即ω⊂Ω且C=∂ω。inside(C)表示区域ω,outside(C)表示区域。假设图像I0(x,y)由两个灰度均匀区域和构成,被检测区域是灰度为的区域,其边界为C0。得出拟合的函数为
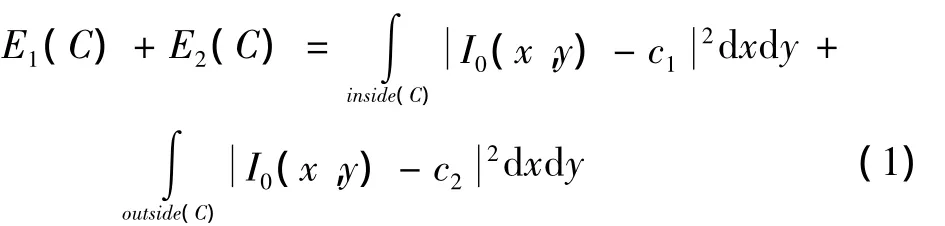
式中:C为闭合轮廓曲线;c1和c2分别是轮廓曲线C的里面和外面的灰度统计均值。显然,当且仅当待分割的目标边界C0才能使上述函数达到最小,即
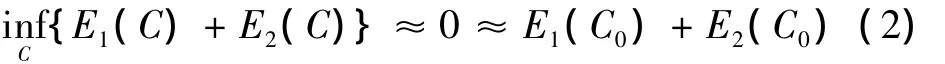
在式(2)的基础上,引入惩罚项概念:第一个为轮廓曲线C的长度项(Length(C)),第二个为轮廓曲线C的内部区域面积(Area(C))。所以C-V模型的整体能量泛函可以表示为
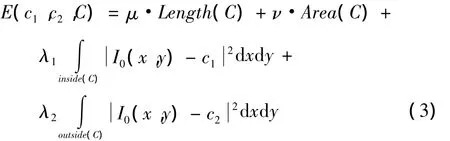
C-V模型在图像分割任务已经取得了良好的效果,此模型有着比较大的收敛范围,能有效处理拓扑结构变化,待检测目标的边缘是不需要通过梯度来定义,相对减少了演化时间,能够得到轮廓相连的目标边缘。然而,它仍然有一些固有的局限性。首先,C-V模型的假设前提是图像的灰度均匀,所在它在对非同质的图像进行分割时,由于是考虑全局的图像信息而演化轮廓曲线,得到的分割结果不是很理想。再次,基本C-V模型一般在逼近非同质的目标时需要迭代次数较多,且得到的结果受往往很不精确,出现误分割[9]。为了解决上述问题,本文提出了改进的算法。
2 改进Chan-Vese模型
2.1 局部核心函数
在现实试验中,经常碰到非同质目标的图像,为了精确地分割出这种图像的目标,本文建立一种新的动态轮廓模型,新建模型运用局部的统计信息,同时延续基于区域分割算法抗噪的特点。此模型在分割图像的时候不依赖全局灰度统计信息,也不同于基于区域的动态轮廓模型中所假设的,即图像中的前景和背景区域可以用全局的统计信息表示。新模型是分别用小的局部区域来描述图像的对立区域,这一系列局部区域的算法要沿着演化曲线上的每个像素点进行,曲线上的像素点都有各自相对应的局部区域。在最小化局部区域的局部能量时,要考虑轮廓上各点的局部区域,轮廓上的各点都朝着最小化它的局部能量的方向演化。演化轮廓将这些局部区域划分为局部内部和局部外部的两个区域来计算这些局部能量。
这里,局部核心函数被直接引入到C-V模型中,它使用局部统计信息来提高对非同质目标的图像的分割能力
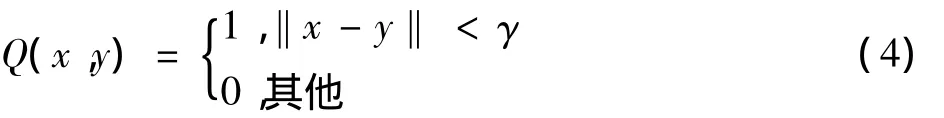
式中:Q(x,y)表征局部核心区域,即当y在以x为圆心、γ为半径的圆内时,核心函数Q(x,y)取1;反之,取0。
2.2 惩罚限制项
在基本C-V模型中,每进行一次过程迭代运算,都要对水平集函数重新初始化,这让C-V模型在运行过程中很费时间[10]。在本文中,不直接使用初始化步骤来保持水平集函数为一个符号距离函数,但是增加一个限制项,见式(5)
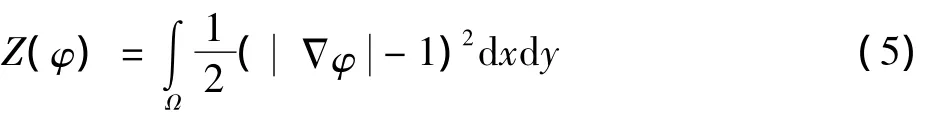
这可以使得水平集函数接近一个符号距离函数。该惩罚限制项是一个度量标准,描述一个函数φ距离一个符号距离函数有多近。此标准在该方法中对于消除重新初始化起到了关键性作用。为了阐述惩罚项的作用效果,给出其梯度下降流方程
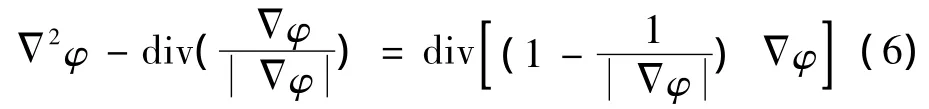
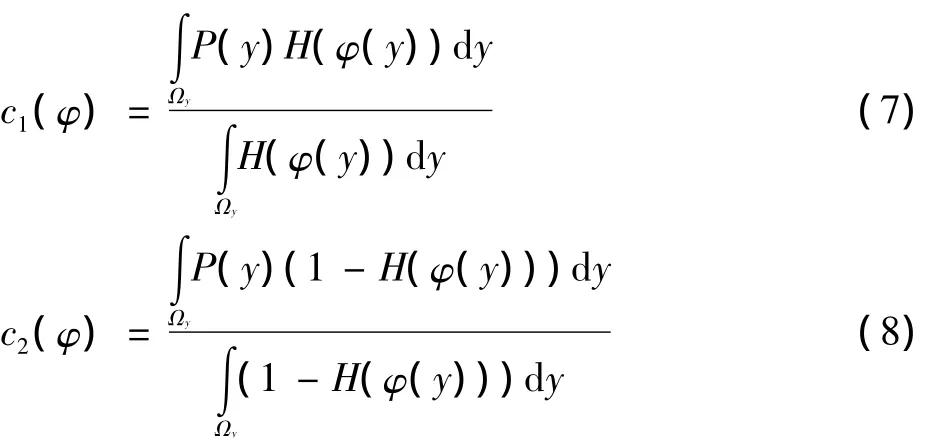
式中:P(y)表示模型参考的是局部灰度统计信息。在上述两式中引入局部限制特性函数,可以将基于全局信息的轮廓内部和外部灰度均值c1(φ)和c2(φ)局部化为如下形式
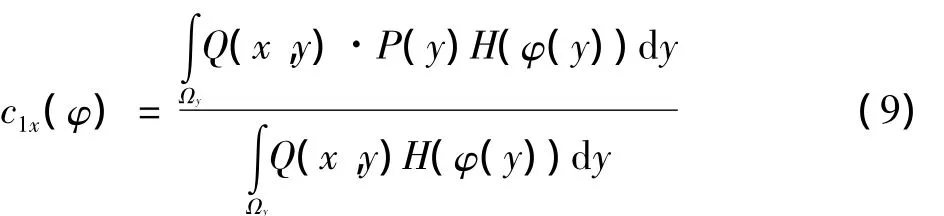
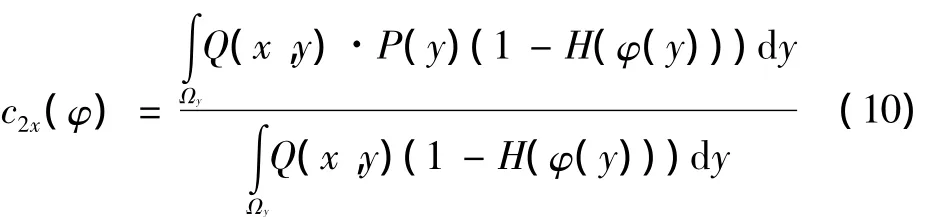
式中:c1x(φ)和c2x(φ)分别表示在轮廓C上的某一个点x处,被Q(x,y)局部化的轮廓内部和外部区域的灰度均值,使用该方法必须分析轮廓上各点的局部灰度统计信息。
根据局部核心函数Q(x,y),局部灰度均值c1x(φ)和c2x(φ),再结合C-V模型的核心函数
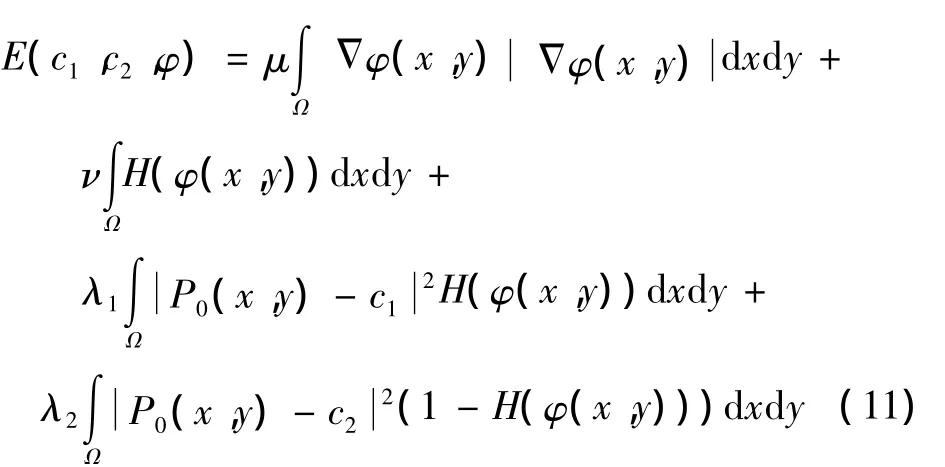
引入局部核心函数之后,加入限制惩罚项,可以构建一个基于局部灰度统计信息的能量
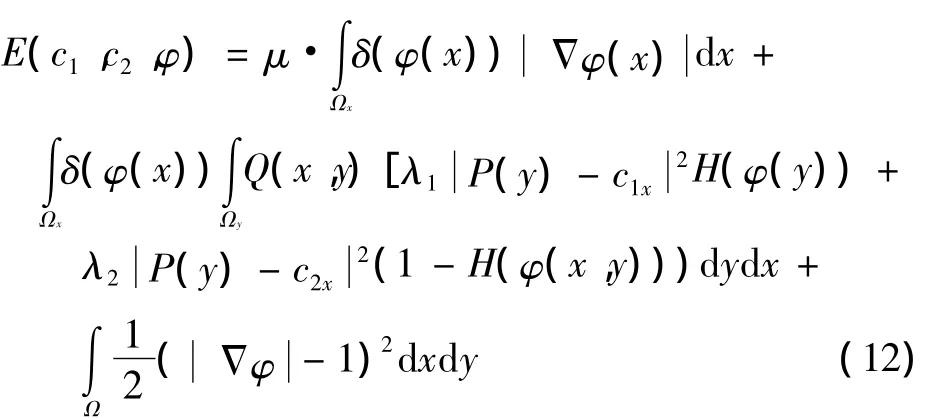
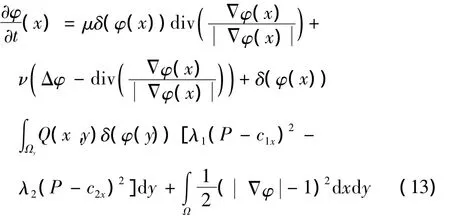
在C-V模型中,当轮廓曲线内部和外部灰度均值近似于全局均值c1和c2时,得到核心函数的最小化。而在本文方法中,当轮廓上每一点不断的演化,直到每一点的局部内部和局部外部均值近似于局部均值c1x和c2x时,得到核心函数的最小化。轮廓上每一点的最终演化结果就是最后的分割边界结果。
3 实验结果与分析
图1a记录了C-V模型和改进的新模型用相同的初始轮廓,对一幅瓷器图像的分割结果,其中新模型的半径参数选取γ=4个像素。瓷器和背景的灰度分布变化较复杂,期望能够分割得到瓷器的轮廓。图1a为初始轮廓的位置,图1b为C-V模型的分割结果,图1c为新模型的分割结果。
图1d记录了C-V模型和新模型以同样的初始轮廓,分别对一幅手骨X光图像进行分割的实验结果,其中本文模型的半径参数选取γ=16个像素。图像中手骨位置的灰度分布不均匀,期望能够分割获得无名指中间指关节的边界。图1d为初始轮廓的位置;图1e为C-V模型的分割结果;图1f为新模型的分割结果。
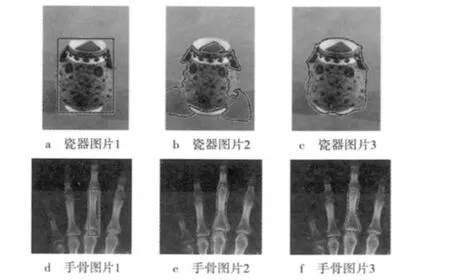
图1 实验结果比较
通过图1可以看出,基于全局灰度统计信息基本CV模型,轮廓曲线演化扩展得过大,图1b的轮廓曲线把背景阴影也当作了目标,图1e中的轮廓停留在两个指关节外,这两个实验中的C-V模型没能得到准确的分割结果;从图1c和图1f可以看出,基于局部核心函数的的改进算法,针对非同质的目标图像,能够将演化轮廓曲线停止在较为理想的边界。这验证了改进的C-V模型在分割非同质图像时有较好的图像分割效果。
4 小结
本文通过分析C-V模型的优缺点,针对基本C-V模型对非同质目标图像的分割效果不理想情况,提出改进模型,在经典C-V模型的基础上加入新的概念,使得模型可以对非同质进行有效分割,同时在原模型中加入的惩罚项能避免水平集函数初始化,加快改进模型的演化时间。但由于水平和时间有限制,本算法还有不足之处,需要进一步深化研究。本算法只能针对两相图像,通过一个轮廓曲线把图像分成两个部分,目标与背景。作为一个双峰模式,此模型不能分割多个目标的多相图像,在以后的研究学习中,将扩展当前模型来处理多相图像。
[1]杨润玲,周军妮,刘利.基于改进型FCM聚类的图像分割新方法人[J].电视技术,2008,31(6):24-31.
[2]刘喜英,吴淑权,徐向民.基于区域生长法的医学图像分割研究[J].电视技术,2003,26(9):24-31.
[3]许新征,丁世飞,史忠植,等.图像分割的新理论与新方法[J].电子学报,2010,38(S1):43-49.
[4]张晶,王黎,高晓蓉,等.数字图像处理中的图像分割技术及其应用[J].信息技术,2010(11):36-43.
[5]MEYER F,BEUCHER S.Morphology segmentation[J].Journal of Visual Communication and Image Representation,1990,1(1):21-46.
[6]ADALSTEINSSON D,SETHIAN J A.The fast construction of extension velocities in level set methods[J].Journal of Computational Physics,1999(148):2-22.
[7]SUM K,CHEUNG P Y.A novel active contour model using local and global statistics for vessel extraction[C]//Proc.EMBS 2006.[S.l.]:IEEE Press,2006:3126-3129.
[8]陈旭锋,谢强军.图像分割中偏微分方程模型解的存在性分析[J].杭州电子科技大学学报,2009,29(4):58-70.
[9]张思维.一种加快的C-V模型分割方法研究[J].天中学刊,2011,26(5):13-16.
[10]李俊,杨新,施鹏飞.基于Mumford-Shah模型的快速水平集图像分割方法[J].计算机学报,1997,25(11):1175 -1183.
