一种基于小波和Wiener相结合图像去噪新方法

李东兵，李国平，滕国伟，赵海武，王国中，罗平伟，李 萍

(1.上海大学通信与信息工程学院，上海 200072;2.上海国茂数字技术有限公司，上海 201204)

责任编辑:时 雯

随着网络、数字多媒体和通信技术的迅猛发展，数字视频图像技术获得了广泛应用，数字视频信息因其视听特性已成为人类获取信息的重要手段之一。伴随着视频压缩编码技术的成熟，视频数据传输速度加快，数字视频业务在生活中得到普及。而视频信息在采集、处理、存储、传输和接收中，会受到干扰信号的影响，导致接收端接收的图像质量下降，影响图像的处理和观赏。在长期的研究中，发现对图像影响较大的噪声有脉冲噪声和高斯噪声。图像去噪研究的重点是噪声的去除和细节边缘保护［1－2］。通过对视频图像处理技术的研究，常用的图像滤波算法有中值、均值，维纳和小波变换滤波等。本文在对经典维纳滤波方法、小波去噪的基础上，提出了新小波变换和自适应维纳滤波方法。

1 常用图像噪声模型和经典去噪方法

1.1 常用图像噪声的模型

虽然噪声出现在图像中的种类各种各样，在研究中，通常按照噪声与图像在数学意义上的关系分类，主要将噪声分为乘性噪声和加性噪声这两类。

加性噪声，即图像和噪声重叠于图像上，使得图像模糊。其中噪声和信号是相互独立的，加性噪声是与信号无关的噪声，是始终存在的噪声。常见的加性噪声有椒盐噪声、高斯噪声等典型噪声。加性噪声模型为

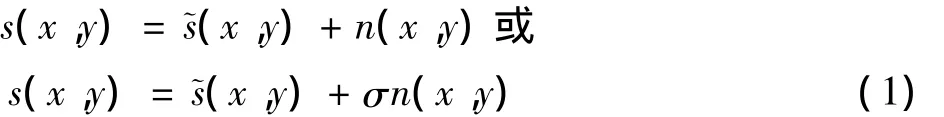
式中:s(x，y)为含噪声图像;～s(x，y)为原图形不含噪声的估计;n(x，y)为高斯白噪声;σ为噪声的方差［3］。

乘性噪声，是由于采样条件不理想而引起的，其与信号的关系是相乘的关系，信号存在时乘性噪声才存在，否则不存在。乘性噪声模型为

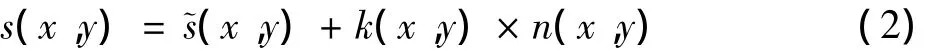
式中:s(x，y)为含噪声图像;～s(x，y)为原图形不含噪声的估计;n(x，y)为高斯白噪声;k(x，y)为乘性噪声系数。

1.2 普通维纳滤波

经典维纳滤波是一种线性滤波方法，可用于噪声中有用信号提取。经典维纳滤波原理是使得原始图像和恢复图像间的均方误差值最小。在经典维纳滤波中，需要计算模板中像素的均值和方差［4－7］。均值为

方差为

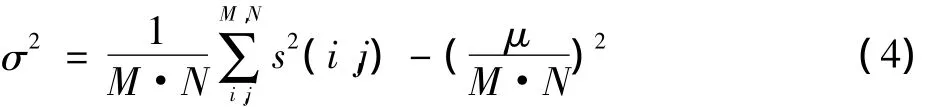
常用的经典维纳滤波方法为

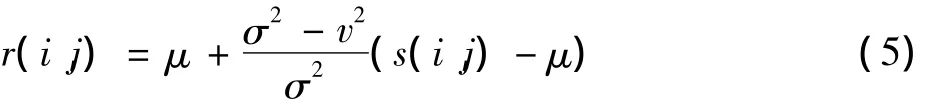
式中:s(i，j)为原始图像;μ为输出像素值;σ2为均值;v为模板均方差值，为噪声均方差值。在式(5)中:

当σ2=v2时，r(i，j)=μ，此时输出值等于模板的均值;

当 σ2≫v2时，r(i，j)≈s(i，j)，此时输出值和原始图像的像素点的灰度值相同;

当 σ2≪ v2时，r(i，j)=s(i，j)－(s(i，j)－ μ)，此时 r(i，j)围绕 s(i，j)值波动。

1.3 小波阈值滤波方法

设有观测信号为

式中:s(t)是原始信号;n(t)是均值为0;方差为σ2的平稳高斯噪声。首先对一维信号f(t)进行离散采样，得到N 点离散信号f(n)，n=0，1，2，…，N －1 。其小波变换为

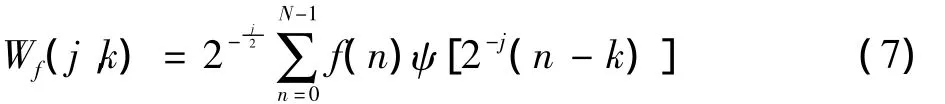
式中，Wf(j，k)为小波系数。在实际应用中，直接利用上式比较复杂，一般Ψ(t)也没有明显常用表达式，所以常用双尺度方程［8－10］

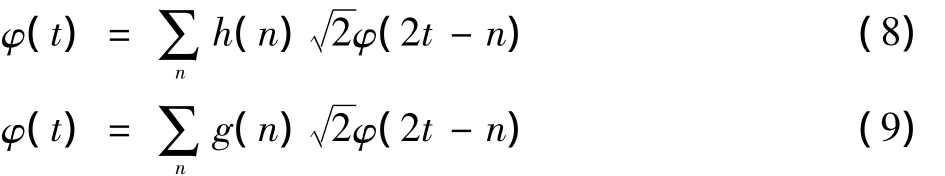
得到小波变换的递归实现方法

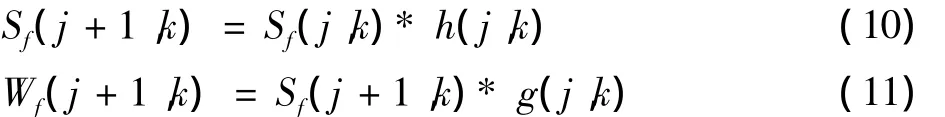
式中:h和g为分别对应的尺度函数和小波函数的低通与高通滤波;Sf(0，k)为原始信号f(k);Sf(j，k)为尺度系数;Wf(j，k)为小波系数。

对于二维图形信号，使用经典的分解方法，在水平和垂直方向通过滤波的方法实现二维小波变换对图像进行分解。图1是将图像进行二层分解的示意图。

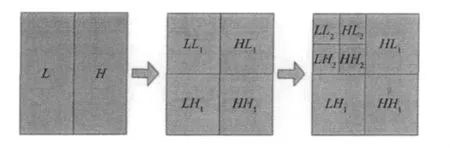
图1 图像的小波二层分解结构

其中，LL子带部分是水平和垂直方向上利用低通小波滤波器卷积后产生的小波系数;HL子带部分是在水平方向上利用低通和垂直方向利用高通小波滤波器卷积后产生的小波系数;LH子带部分是在水平方向利用高通和在垂直方向上利用低通小波滤波器卷积后产生的小波系数;HH子带部分是在水平和垂直方向利用高通小波滤波器卷积后产生的小波系数。

针对小波变换的线性特性，使用高低通滤波方法，使得信号小波系数和噪声小波系数相分离，从而可以通过设置阈值，去除噪声部分，保留信号有用系数部分，达到滤波的效果。

2 小波变换与自适应维纳相结合的新滤波算法

2.1 新自适应维纳滤波方法

针对于常用维纳滤波方法模板过于单一。不方便统计噪声等特点，本文提出了一种新自适应维纳滤波的方法。其实现了滤波模板可以在给定的几个或多个模板中，挑选出最佳的滤波模板，然后在此模板下，得到每个点的最佳滤波效果［11］，其实现过程如下。

新自适应维纳滤波过程是从单个像素点的滤波出发实现图像滤波。在图像滤波过程中，依次计算每个像素点的N(N从3开始，最大为2i+1)阶局限窗口内的像素点的平均均值和方差。在计算的i阶结果中，选择平均均值和方差最小的窗口模板作为最终滤波处理模板。

通常，4阶滤波窗口即可达到理想效果。如图2所示，灰色区域为该阶时所需处理的像素点［12－14］。

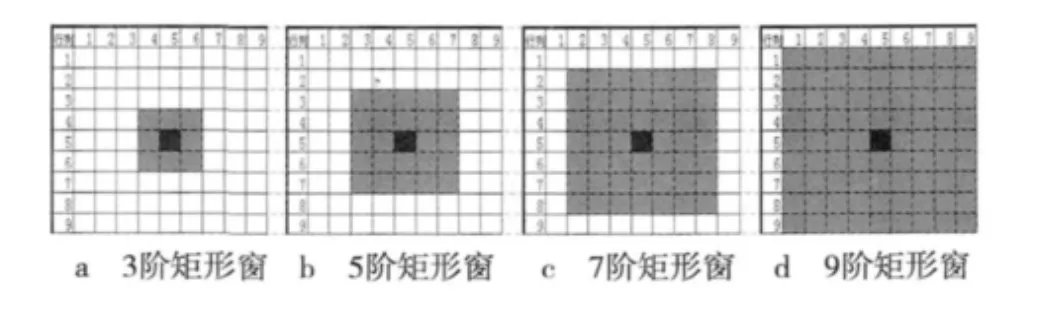
图2 滤波窗口选择方法

在本文处理过程中，对式(6)进行了改进，即

式中:q= σavg/(σvar+1);Δ = σvar/(σavg+σmax+1);σavg为矩形窗中像素方差和的平均值;σvar为矩形窗中心的像素点的方差值;σmax为图像中方差值最大的值。

2.2 新滤波算法描述

本文主要采用的方法是:在图像进行小波分解后，分别针对分解后的LL，LH，HL和HH部分进行处理。由于LL部分是图像的信息主要部分，可以对LL部分进行二次分解，以便更好地滤除噪声对细节的影响。针对LH，HL和HH部分，直接对其进行小波阈值滤波和自适应维纳滤波，减少噪声对图像细节的影响。滤波过程如图3所示。

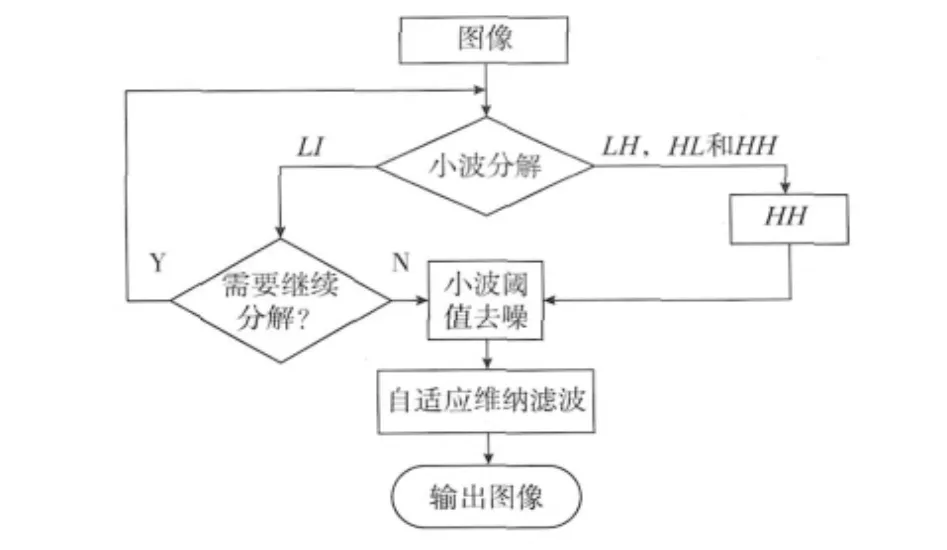
图3 图像滤波处理流程图

3 实验结果

3.1 主观对比

通过对带有加性高斯噪声的Sussie图像进行去噪后，其结果如图4所示。

图4 图像滤波结果

图4a图像为带有高斯噪声的Opening图，图4b是经过小波滤波处理后的结果，图中残留有图片平滑后的噪声痕迹。图4c是经过经典维纳滤波处理后的结果，在图像边缘部分出现了较强的模糊。图4d是新自适应滤波处理的结果，可以看出，新自适应滤波方法可以较好地进行图像滤波，并保留图像的轮廓信息。

3.2 客观对比

图像结构相似度指数(Structural Similarity Index，SSIM)是一种衡量两幅图像相似度的新指标，其值越大越好，最大为1［15］。在本文中采用YUV图像序列，图像带有高斯噪声(噪声的均值为 0，方差分别为0.003，0.004 和0.005)，进行(3·3)，(5·5)，(7·7)，(9·9)窗的维纳滤波、小波阈值滤波和新自适应滤波后，分别计算出SSIM。代码在VC6.0环境下编译，通过实验对比，结果如表1所示。

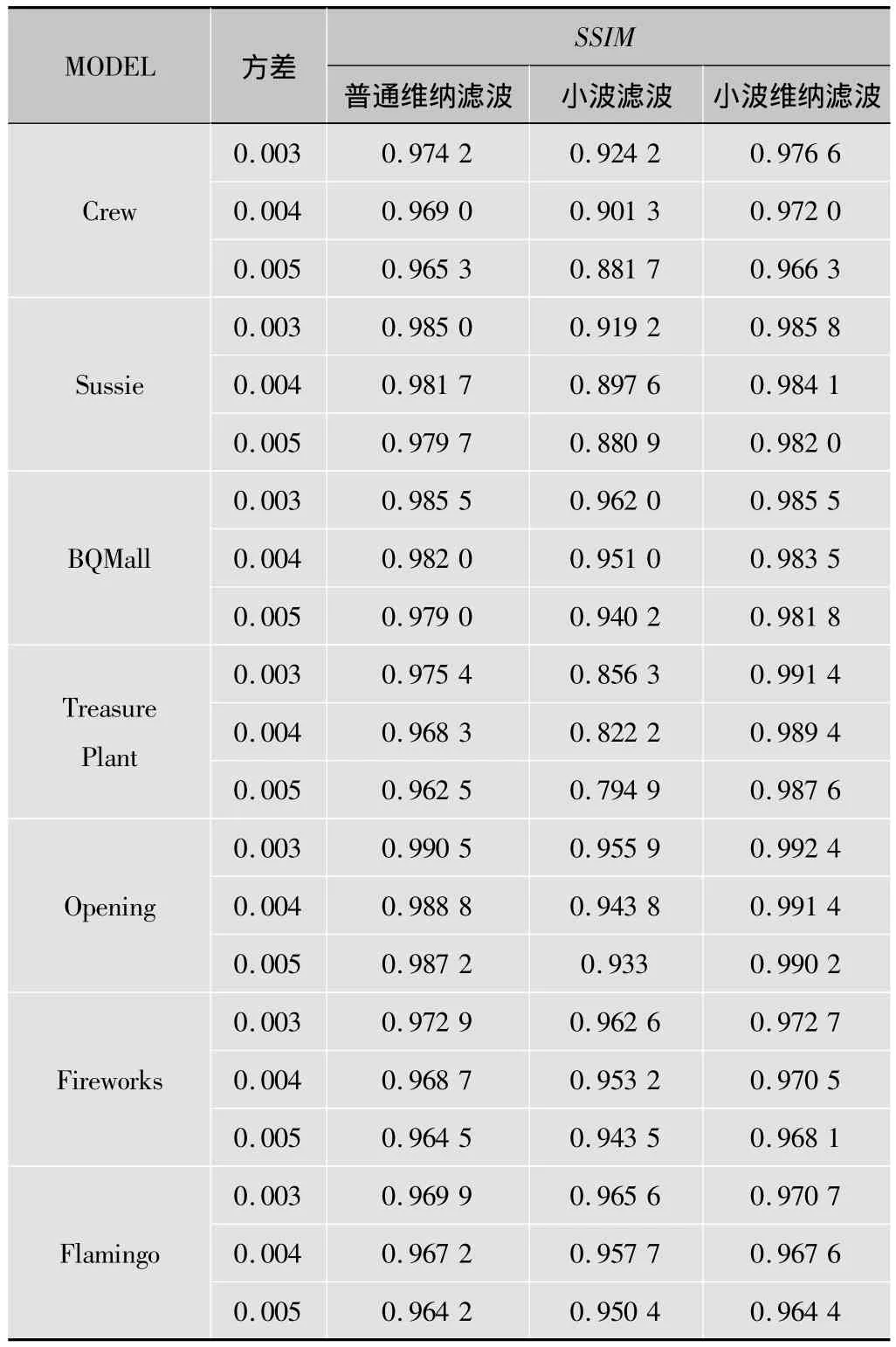
表1 均值滤波、维纳滤波、自适应维纳滤波SSIM

4 小结

本文结合维纳滤波和小波变换的优点，从而提出了一种小波变换与自适应维纳相结合的新滤波算法。算法揉合了小波变换实现快捷及易于处理，很容易地将高频与低频信号量的特性及方便剔除各个部分中的噪声分量，结合维纳滤波在处理细节方面的有点，使得算法整体上处理包容了图像高低频和主体与细节方面的内容。它可以根据图像特性进行自适应的选择模板滤波，并达到较好的滤波效果。

［1］王民，文义玲.常用图像去噪算法的比较与研究［J］.西安建筑科技大学学报，2010，42(6):895－898.

［2］龙振弘.数字图像去噪典型算法的分析比较［J］.福建广播电视大学学报，2009，(1):67－69.

［3］王俊芳，王正欢，王敏.常用图像去噪滤波方法比较分析［J］.现代商贸工业，2009，16(1):310－311.

［4］李俊盛，刘宗田.基于异性扩散—中值滤波的超声医学图像去噪方法［J］.计算机应用于软件，2009，26(1):76－78.

［5］YANG Y，WEI Y.Wiener filtering using neighboring coefficients［C］//Proc.2011 International Conference on Network Computing and Information Security.Guilin:IEEE Press，2011:406－409.

［6］ROBERT D，MARKUS R.Stability analysis of an adaptive wiener structure［C］//Proc.ICASSP 2010.Dallas:IEEE Press，2010:3718－3721.

［7］SUI C H，TANG Y J.Image regressing technique research of astronomical blurring images－astronomical image regressing based on wiener filtering［C］//Proc.ICISE 2009.Nanjing:IEEE Press，2009:1294－1297.

［8］COIFMAN R，MEYER Y，WICKERHAUSER V.Wavelet analysis and signal processing［C］//Wavelets and their applications.［S.l.］:Boston.Jones an Bartlett，1994:125－151.

［9］杨兴明，吴永忠，孙锐，等.基于小波多分辨率分析和新的阈值自适应的信号去噪［J］.合肥工业大学学报，2007，30(12):1580－1583.

［10］郭蕾，田松，许悦雷，等.一种小波自适应比例萎缩去噪改进算法［J］.电视技术，2012，36(11):27－30.

［11］YI X F，CHEN F J，YANG X J.Template matching by wiener filtering［J］.Journal of Computer Research ＆Development，2000，37(20):1499－1503.

［12］HARDIE R.A fast image super－resolution algorithm using an adaptive wiener filter［J］.IEEE Trans.Image Processing，2007，16(12):2953－2964.

［13］JIN F，FIEGUTH P，WINGER L，et al.Adaptive wiener filtering of noisy images and image sequences［J］.IEEE Trans.Image Processing，2003，3(1):349－352.

［14］李东兵，李国平，滕国伟，等.一种新的自适应维纳滤波方法［J］.上海大学学报，2012，18(6):555－560.

［15］WANG Z，BOVIK A C，SHEIKH H R，et al.Image quality assessment:From error visibility to structural similarity［J］.IEEE Trans.Image Processing，2004，13(4):600－612.