改进PSO算法在图像配准中的应用

王 鹤，谢 刚

(太原理工大学信息工程学院，山西 太原 030024)

责任编辑:时 雯

图像配准是指对不同时间、不同场景的多幅图像进行空间上的几何变换，这样就使得代表相同的结构像素在空间上达到一致性［l－2］。过去的几年来，该技术得到了迅猛的发展。就图像配准步骤而言，它一般包括3个步骤:首先，确定配准图像与浮动图像的坐标系，并且定义坐标系之间的关系;其次，定义相似性测度作为判别准则;最后，应用优化算法。其中，第2步与第3步是图像配准的核心。图像配准的方法一般可以分为2种:基于图像特征和基于图像灰度［3］。第1种方法是通过查找图像之间共有的并且比较明显的特征来进行参数变换。这种方法的优点是简单并且计算效率高，然而配准的精度很大程度上要依赖于图像特征点的正确提取［4－5］。但有时侯因为图像比较复杂，计算机自动准确提取特征点是比较困难的，这就需要人工辅助来完成特征点的选取。然而，对于基于图像灰度的配准方法只是利用了图像间的灰度相似性来完成配准。由于此方法充分利用了图像灰度信息，因此，配准准确度一般比较高。

1 标准PSO算法

Kennedy等人［4］提出了粒子群优化算法。此算法是来自于对生物群体的研究，该算法指出每一个优化问题的潜在解都可以被当做搜索空间中的一个粒子，并且每一个粒子的适应值都是由一个待优化的目标函数来决定的，每一个粒子都有自己的飞行速度，它们的运行方向和距离都是由这个速度决定的。粒子跟随当前的最优粒子在解空间中进行搜索，在此过程中，所有的粒子会共享它们得出的最优解信息，进而利用它们的记忆来调整自己的速度和位置，不断地进行比较，直到最终发现最优解。

假设S维空间搜索空间，其中粒子群规模为M，对于粒子群中的Xi(xi1，xi2，…，xid)则表示第i个粒子的位置，而 Vi(vi1，vi2，…，vid)表示的是第 i个粒子的速度。Pbest(bi1，bi2，…，bid)则代表的是第i个粒子目前可以搜索到的最优位置。对于整体粒子群目前为止可以搜索到的最优位置则用Pgb(Pgb1，Pgb2，…，Pgbd)进行表示。就每一代粒子而言，它的第d维速度与位置则按式(1)变化

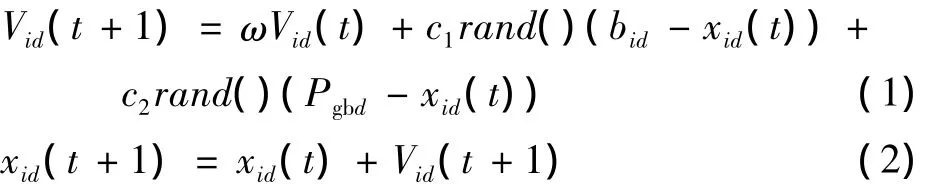
式中:1≤i≤N，1≤d≤D;c1和c2则是常数被称为学习因子;rand()表示0～1之间的随机数。通常c1=c2=2，ω为惯性权重系数，在本文中ω取值为0.729。并且可以根据搜索空间的维数S来求得粒子群的规模M，即

标准PSO算法的优点［5］是可以在短时间内得到高质量解。但是，它在进化过程中比较容易陷入局部最优解，使得配准精度下降。马军杰等［6］与张海峰等［7］曾对标准PSO进行改进。本文提出的算法在对标准PSO算法改进的同时并分别与二者相比较。

2 PSO算法改进

粒子在飞行过程中，当某粒子发现了一个当前最优解时，其他粒子便会向其靠拢。但是如果该位置是局部最优点而不是全局最优解时，就会出现所谓的“早熟”现象，为了克服这一现象，在这里提出了一个评价判断标准——粒子相似度δ(t)

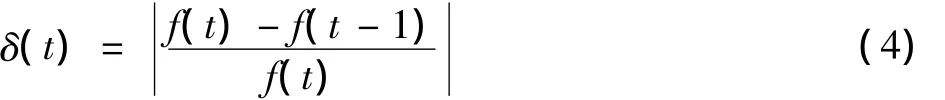
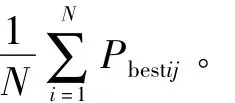
此时，式(2)不变，式(1)则为

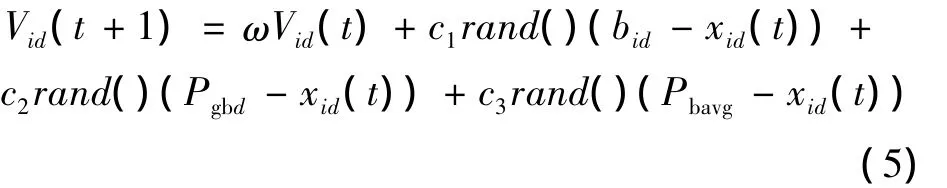
其中c3取值为2，其他参数保持不变。

对PSO进行改进后的算法流程图如下图1所示。

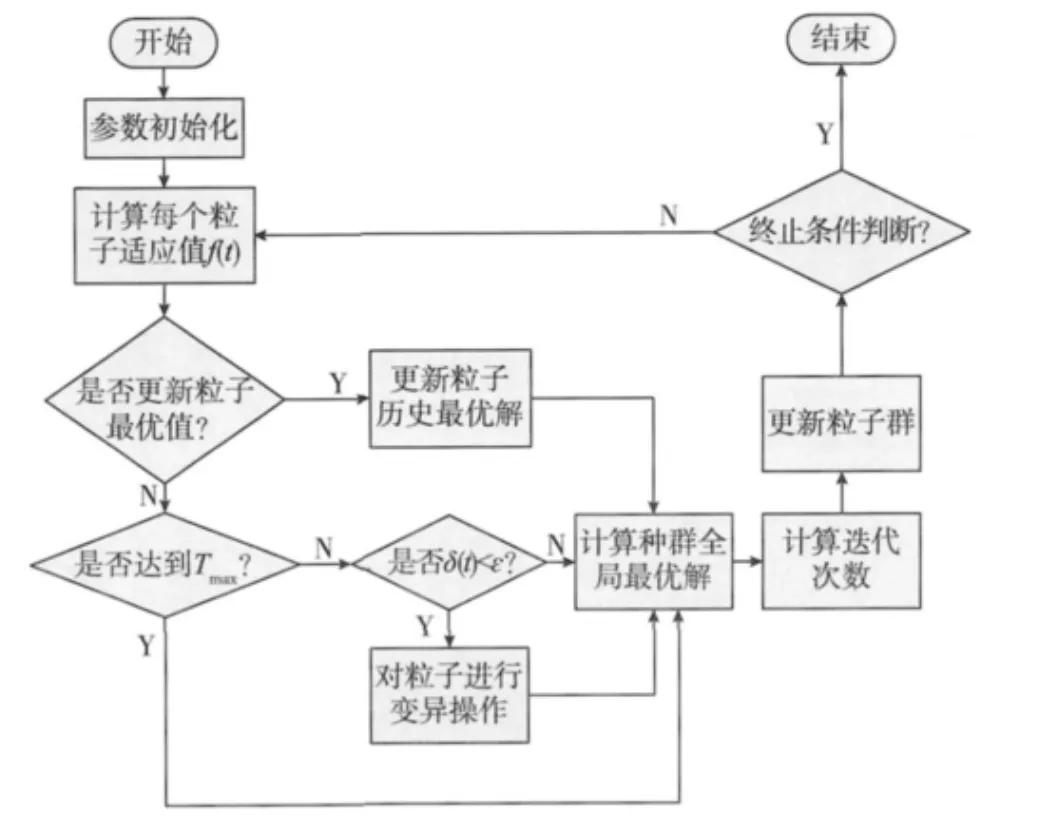
图1 改进的PSO算法流程图

3 图像的相似性测度

对于配准的评价标准，称之为相似性测度。本文选用峰值信噪比 PSNR作为相似性测度准则［8］。由于PSNR不仅可以作为用来衡量图像灰度质量的标准，并且它可以直接从整体上反映两幅图像灰度上的差异.因此目前得到广泛应用。对于相似性测度PSNR来说，当PSNR值增大时，表示的是两幅图像的灰度差异变小，此时图像比较相似，图像的恢复质量越高;反之，则表示两幅图像灰度差异很大并且相似度不高，恢复图像的质量比较差。传统PSNR定义为

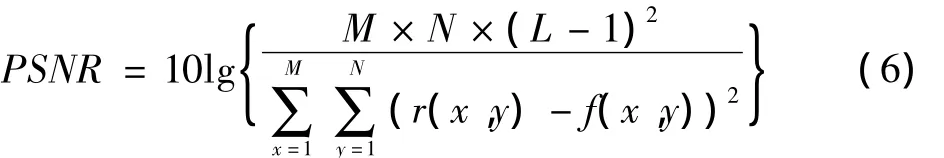
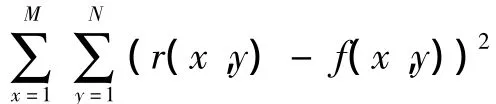
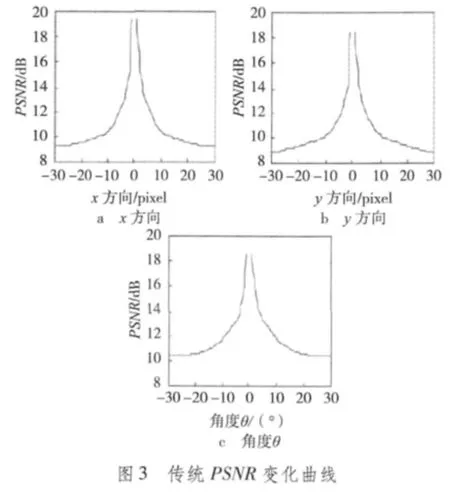
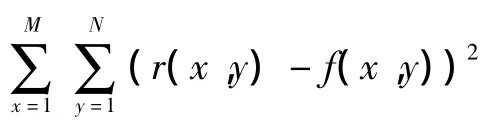
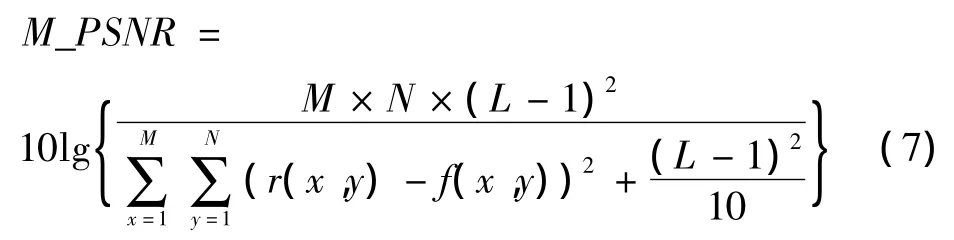
由式(7)再次对图2进行自配准，从而得到如图4所示的M_PSNR变化曲线。从图4可知，M_PSNR曲线光滑连续无断点。

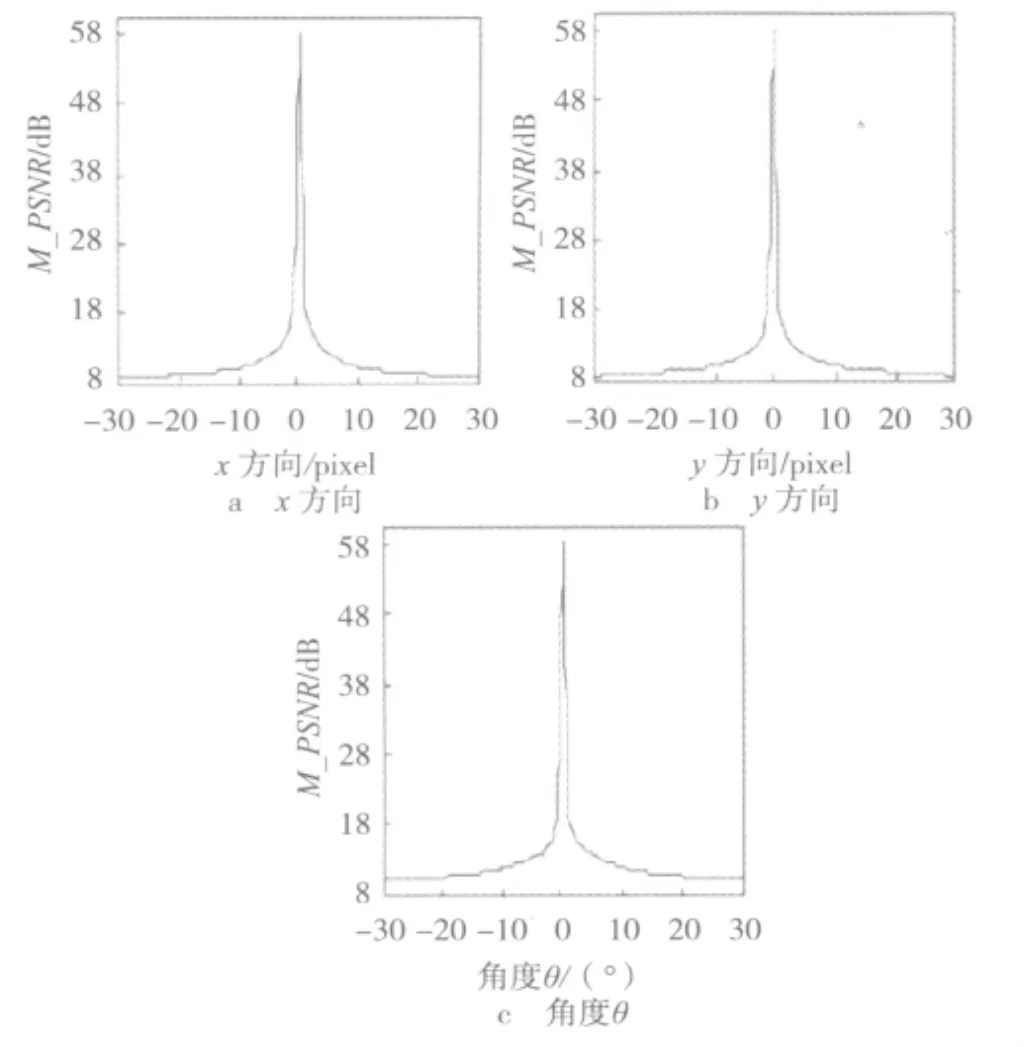
图4 M_PSNR变化曲线

选定相似性测度M_PSNR之后，应用本文提出的算法对相似性测度在x方向、y方向和θ方向进行搜索优化。

4 模拟实验结果分析

为了证明本文提出的算法的优良，在这里将会用文献［6－7］所用的方法与文中方法比较。并且为了方便比较，使用η配准精度作为配准指标

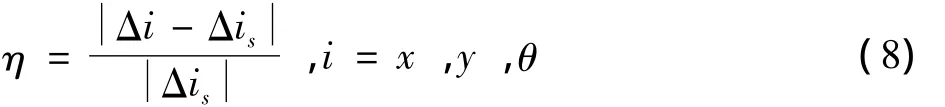
式中:Δis为变换参数真实值;Δi为变换参数的实际值。

实验中选取image－001的图像作为参考图像，如图5a所示。对参考图像做表1的变换得到image－002和image－003。

图5 image的参考图像和浮动图像

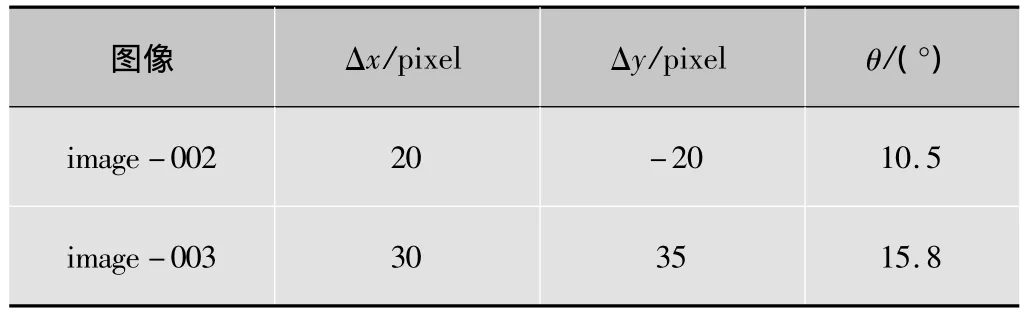
表1 浮动图像的变换参数

实验结果如图6、图7所示。

图7 image－003实验结果

3种方法分别对于image－002，image－003配准误差比较如图8、图9所示。

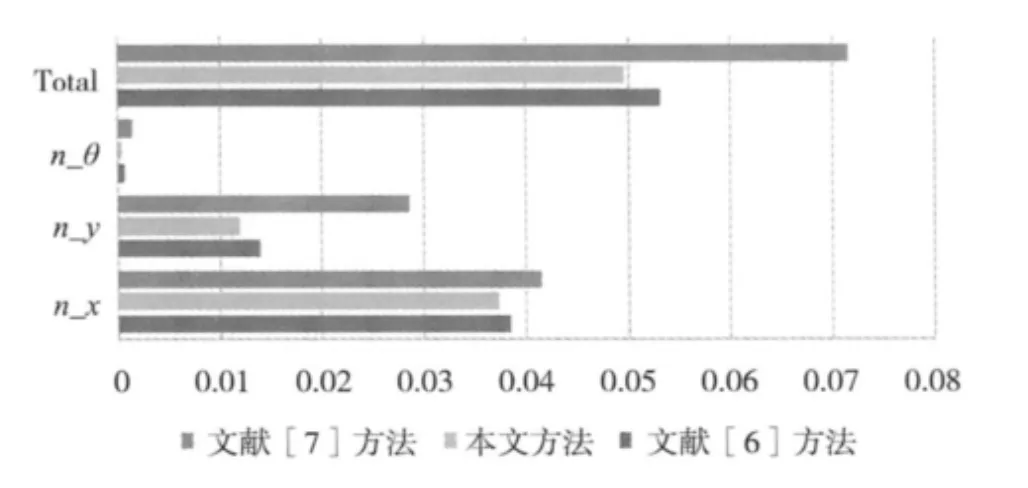
图8 image－002配准误差比对图

从以上图表可知:文中提出的方法不仅在在x方向和y方向上的平移误差均占有一定的优势，在旋转方面仍略胜一筹。不仅如此，从总体误差来看，文中提出的方法精度要更高一些。因此，这是一种有效的优化算法。

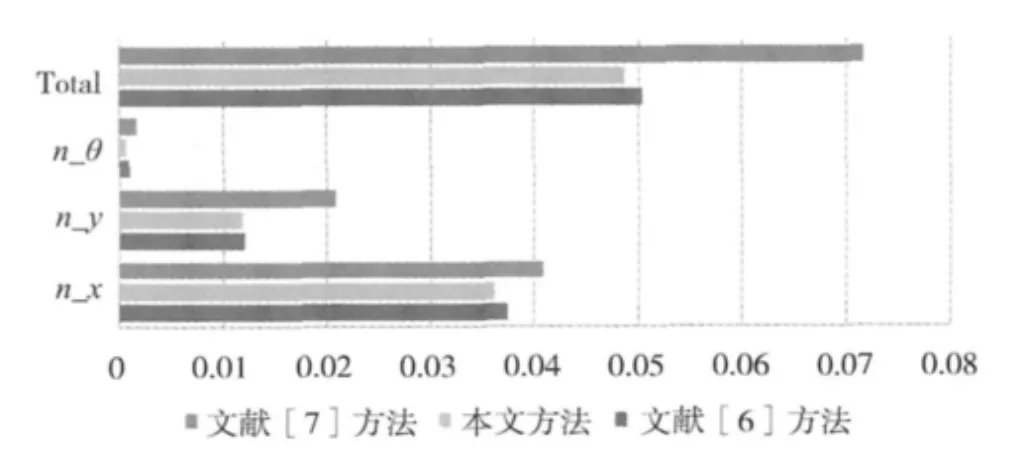
图9 image－003配准误差对比图

5 结论

为了解决标准PSO容易陷入局部最优解的“早熟”问题，本文提出了改进PSO优化算法。通过实验的对比表明，文章中提出的算法配准精度高、误差小。对于图像配准具有很好的实际操作意义。在今后的研究工作中，可以以此展开工作来完善图像配准精度。

［1］HAROLD S S，ROBERT W.Blind cross－spectral image registration using profiteering and ourier－based translation detection［J］.IEEE Trans.Geoscience and Remote Sensing，2002，40(5):637－650.

［2］SHANG L F，LV J C，ZHANG Y.Rigid medical image registration using PCA neural network［J］.Neurocomputing，2006，69(5):1717－1722.

［3］李磊.医学图像配准的研究及应用［D］.吉林:吉林大学，2011.

［4］PLUIM J，MAINTZ J，VIERGEVER M.Mutual－information－based registration of medical images［J］.IEEE Trans.Medical Imaging，2003，22(6):986－1004.

［5］李玲玲.像素级图像融合方法研究与应用［D］.武汉:华中科技大学，2005.

［6］马军杰，尤建新，陈震.基于改进粒子群优化算法的灰度神经网络模型［J］.同济大学学报，2012，40(6):740－743.

［7］张海峰，梁工谦，张晶.基于粒子群优化模糊神经网络的高技术知识创新评价［J］.系统工程与电子技术，2012，34(2):973－975.

［8］盘梅森，汤井田，杨晓利.采用PCA和PSNR的医学图像配准［J］.红外与激光工程，2011，40(5):356－363.