基于混沌二进制粒子群算法的配电网重构研究

邓桂秀，江修波，蔡金锭

(福州大学 电气工程与自动化学院，福建 福州 350108)

0 引言

配电网具有闭环设计、开环运行的特点。网络重构即在保证配电网连通且辐射运行状态下，选择电网中开关的不同开合状态，使配电网的某些指标达到最优运行方式。其主要作用为以下3点:降低网络损耗、均衡负荷、平衡过载和快速恢复供电，提高可靠性。

配电网重构的方法也多种多样。目前，较多使用的方法主要有3类:数学优化算法、启发式算法、人工智能算法。数学优化算法虽然可得到全局最优解，但是易产生严重“维数灾”，计算时间长。启发式算法计算快速，且分析直观，但往往只能找到局部最优解。

在人工智能算法中，模拟退火法于1983年由Kirkpatrick等人首次应用于求解组合优化问题。该方法能有效解决混合优化问题[1];但该方法对参数和退火方案的依赖性大，计算量大。遗传算法这一搜索方法以自然基因选择机理为基础，此法易产生大量不可行解，影响求解速度。粒子群算法的全局寻优能力不是特别理想，容易产生“早熟”问题。目前应用于配网重构的方法很多，并各有优缺点，所以大多数文献是在基本算法上进行改进。本文算法以二进制粒子群算法为基础，结合了混沌算法，并将新算法应用于配网重构问题的研究。

1 数学模型

配网重构的目标函数:以线损最小、负荷均衡、平均供电不可靠率最低、综合费用最低等为目标函数。以线损最小为目标函数为例，其目标函数为:

式中:Nb为网络中支路总数;Ui，Pi，Qi，Ri分别表示支路bi的末端电压、有功、无功和电阻[2]。

约束条件有变压器等的容量约束St＜Stmax、线路最大电流约束Ii＜Iimax、电压降落约束Uimin≤Ui≤Uimax和供电路径约束，即重构后的网络不能出现逆向供电的情况[3]。

2 混沌二进制粒子群

2.1 二进制粒子群

粒子群算法(Particle Swarm Optimization，PSO)是一种基于迭代的多点随机搜索优化算法[4]。假设在一个N维空间进行搜索，第i个粒子的位置、速度、个体极值和群体极值可分别表示为xi=(xi1，。根据目标函数计算Xi对应的适应度值。个体极值和种群极值分别表示为:

粒子更新速度和位置的公式为:

为解决一些离散组合优化问题，1997年文献[5]在基本粒子群基础上提出了二进制粒子群BPSO(Binary Particle Swarm Optimization，BPSO)算法。在BPSO算法中，粒子每一维位置被限定为0或者为1，粒子的速度是根据Sigmoid函数来更新的。

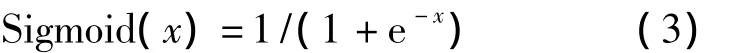
BPSO算法的位置更新公式为:

2.2 惯性权重的混沌映射

混沌 (Chaos)是一种非线性现象，它广泛存在于自然界中。混沌因其便利性、随机性，且对初始条件很敏感，且混沌优化实现简单，寻优效率高等特点而得到学者深入研究[6]。在BPSO算法中，惯性权重ω体现的是粒子继承先前的速度的能力，且较大的惯性权重有利于进行全局搜索，小的惯性权重利用局部搜索。因此，每次迭代过程中，使用混沌映射来确定BPSO算法的惯性权值，避免BPSO算法陷入局部最优，强化全局最优的搜索能力。本文采用Logistic函数来产生混沌变量，其公式如下:

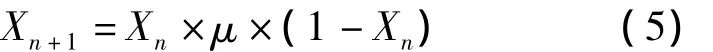
式中:状态量 μ∈[0，4];系统控制参数 X∈[0，1]。当X∈[0，1]时，Logistic映射工作处于混沌状态;也就是说，有初始条件X0在Logistic映射作用下产生的序列是非周期的、不收敛的，当u∈[3.571448，4]时，Logistic映射处于混沌状态。特别是当u=4时，处于完全混沌状态。随着参数μ的增加，Logistic系统最终达到混沌，如图1所示。

图1 Logistic映射分叉示意图Fig.1 Mapping bifurcation diagram of Logistic

混沌变量具有随机性、遍历性和对初值敏感等特点。因此，将混沌变量作为惯性权重时有以下特点:

(1)本文将Logistic函数映射到惯性权重中，因此，所构造惯性权重是一个非线性函数，提高了粒子对环境的认识能力。

(2)混沌变量具有随机性，Logistic函数在μ的取值符合3.569 945 6＜μ＜=4的条件时，迭代生成的值是出于一种伪随机分布的状态，提高了粒子的搜索能力。

(3)混沌变量具有遍历性，能不重复地对空间每个状态进行搜索;因此作为惯性权重时，能有效避免算法陷入局部最优。

2.3 基于混沌二进制粒子群的配网重构

本文在进行网络重构时，采用二进制编码。开关状态作为变量，0表示开关断开，1表示开关闭合。每个开关占据二进制粒子的一维，各开关状态组合在一起形成了一个粒子。潮流计算模块采用前推回代方法计算潮流，计算所得网络损耗作为二进制粒子群算法的适应值。进行网络重构时应保证网络呈辐射状，本文采用生成树的方法，确保电网辐射状运行。配网重构计算步骤如图2。

图2 基于混沌二进制粒子群算法的配电网重构中流程图Fig.2 The flow chart of distribution network reconfiguration based on chaos binary particle swarm optimization

3 算例分析

以IEEE33配电系统 (图3)为例。IEEE33单电源配电系统中有37条支路 (包括5条联络开关支路)，有33个节点，网络首端基准电压12.66 kV，网络总负荷3 715 kW+j2 300 kVA。

图3 IEEE33配电系统接线图Fig.3 The IEEE33 distribution system wiring diagram

分别采用二进制粒子群算法、混沌二进制粒子群算法进行重构，结果如表1所示。

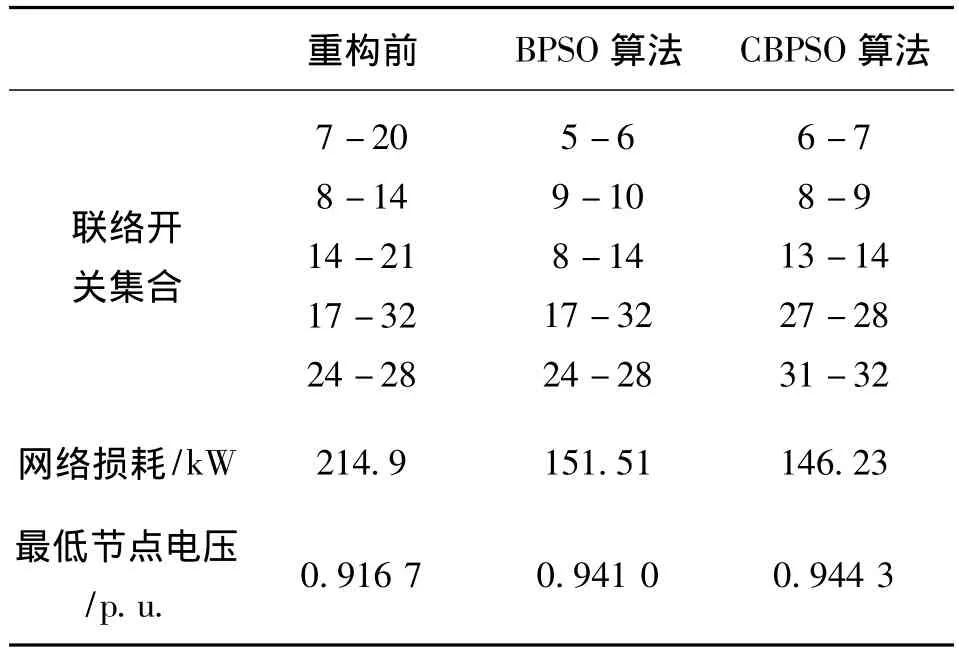
表1 配电网重构结果Tab.1 Results of distribution network reconfiguration

由表1可知，重构前，打开开关7－20，8－14，14－21，17－32，24－28，计算得网络损耗为214.9 kW;运用CBPSO算法得到重构后开关集合为6－7，8－9，13－14，27－28，31－32，有功损耗降至146.23 kW，降低了31.95%。网络重构前后，最低节点电压由0.916 7提升至0.944 3。重构前后IEEE33节点系统节点电压标幺值如图4所示。由此可见，本文采用的CBPSO算法比BPSO算法具有更高的准确度。

图4 IEEE33节点系统各节点电压对比图Fig.4 Comparison the voltage of the IEEE33-node system node

4 结束语

本文将混沌映射引入二进制粒子群算法中进行网络重构，与单纯二进制粒子群算法进行对比，其优点是改善了二进制粒子群容易陷入局部最优的缺陷，提高了解的精度。实验结果表明，引入混沌映射的二进制粒子群具有比二进制粒子群算法更好的效果，降低了网络损耗，提升了最低节点电压值。该方法具有优越性和可行性。