采购拍卖中保留价的策略性披露

黄 毅，胡二琴

（湖北工业大学理学院，湖北 武汉430068）

保留价也被称为底价.在正向拍卖中，保留价是最低限价，若所有投标人的报价低于保留价，拍卖将无法顺利成交；在采购拍卖（即逆向拍卖）中，保留价是最高限价，若所有投标人的报价高于保留价，拍卖也无法顺利成交.20世纪80年代以来，许多学者（如 Milgrom、Maskin、Reliy、Simuleson等）对拍卖中保留价的问题进行了研究，涌现了大量的经典文献［1－7］，但这些文献大都是研究各种拍卖中最优保留价的设定.1993年，Carey从策略性披露的角度探讨了采购拍卖中保留价的公开与隐藏对采购成本的影响［8］.公开保留价是指拍卖人在投标人报价前就把保留价公布出来；而隐藏保留价是指拍卖人在投标人报价后再宣布保留价格.保留价的公开与否直接影响着投标人的信息，从而影响着投标人的报价策略以及拍卖人的收益.Carey指出：在第一价格密封拍卖中，隐藏保留价总能降低采购成本.在公开保留价时，成本高于保留价的供应商不会参加报价，因此实际参与报价的供应商人数是随机的而不是确定的，Carey用参与报价的供应商的平均人数代替实际人数进行分析.文献［9］指出，这种将实际参与报价供应商人数确定化的方法是不必要的，并讨论了保留价公开时的报价策略，指出Carey文中的部分错误，但是文中给出的报价函数有误.同时，文献［8］与文献［9］都只是从数值模拟的结果来比较公开保留价与隐藏保留价时的采购成本，而未能给出严格的数学证明.

本文在文献［8－9］的基础上，进一步研究了采购拍卖中采购商的保留价披露策略，推导了保留价公开与隐藏时供应商的报价策略以及采购商的期望采购成本，并给出了两种情况下采购成本比较的数学证明，并指出文献［8－9］都过分估计了隐藏保留价的作用，若采购商设定的保留价很小，隐藏保留价必然会导致采购失败，主张公开保留价.同时，文献［8－9］都只考虑了第一价格密封拍卖的情形，而本文不仅考虑了采购商的保留价披露策略，同时也研究了拍卖方式的选择.

1 模型

采购商打算用拍卖的方式来采购一个不可分物品，有n个供应商参与报价.每个供应商的成本是他的私人信息，其他供应商只知道他的成本服从区间［a，b］上的某一分布，分布函数为F（x），分布密度为f（x）.假设供应商的成本相互独立，且供应商是风险中立的.由于资金约束等原因，采购商设立最高限价即保留价r.因为最高成本的供应商的报价最高且为b，故r＞b时保留价没有意义.若r＜a，所有的供应商都不会参与报价，故可设r∈ ［a，b］.若报价中的最低报价小于保留价，则报价最低者胜出；否则交易失败，供应商收益为0.供应商希望最大化其收益，而采购商希望最小化其采购成本.现在，采购商面临双重选择：为了减小采购成本，到底该选用第一价格密封拍卖还是第二价格密封拍卖，到底该公开保留价还是隐藏保留价.

2 第一价格密封拍卖的保留价分析

在第一价格拍卖中，若最低报价小于保留价，则报价最低者赢得拍卖，并按照报价获得支付.下面在拍卖前公开与隐藏保留价两种情况下，讨论供应商的报价策略以及采购商的期望采购成本.

2.1 隐藏保留价

当隐藏保留价时，供应商知道采购商设定了一保留价，但并不知道保留价的确切值.因此所有供应商都会参与竞价而不用去考虑保留价，并依照自己的成本来报价βi（c）.显然成本越高报价越高，所以假设βi（c）是可微的单调增函数.由于供应商对称，故假设所有供应商采用同一个报价函数βi（c）＝β（c）.

为了确定β（c），假定其他供应商都按此对称均衡报价，而供应商i的成本为c，选择报价p＝β（x），其期望收益

在对称均衡中，当x＝c时，供应商的期望收益最大.故

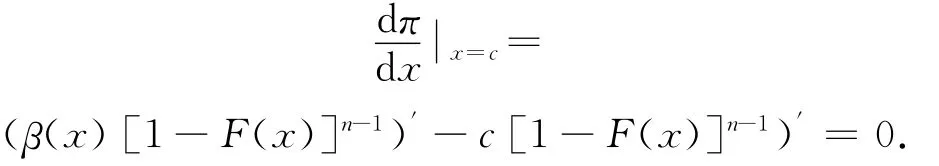
所以报价函数β（c）满足微分方程

而具有最高成本的供应商的报价必为b，即β（b）＝b.在约束条件（2）下，解微分方程（1）得，报价函数

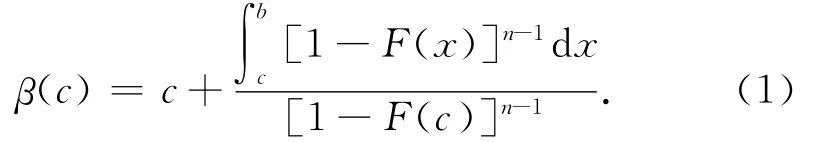
由于报价函数为成本的单调递增函数，所以成本最低的供应商报价最低.记c1为n个供应商中的最 低 成 本，其 密 度 为 n ［1－F（c）］n－1f（c），c ∈［a，b］.由于采购商设定了隐藏的保留价r，所以只有当最低报价r，即c1＜β－1（r）时，交易才会成功，采购商支付β（c1）.

因此采购商的期望支付

特别的，当成本c服从［a，b］上的均匀分布时，由式（1）可得，供应商报价函数

由上式可得，当采购商隐藏保留价时，所有供应商的报价都会高于，因此当保留价满足a≤r时，所有供应商报价都高于保留价，交易不会成功，采购商的期望支付为EFC＝0.

2.2 公开保留价

当采购商在拍卖前公开保留价r时，那么成本高于保留价r的供应商将不会报价.此时实际参与报价的供应商人数是一个随机数ξ，且ξ服从参数为二项分布B（n，F（r））.文献［8］用Eξ代替实际参与报价供应商人数，从而计算供应商胜出的概率.这个其实是不需要的.所有成本不高于r的供应商都会参与报价，并且报价时处在对称位置，因此可假定他们都按照对称均衡γ（c）报价.为了确定γ（c），假定其他参与报价的供应商都按此策略报价，而供应商i的成本为c＜r，但却报价γ（x），由全概率公式可得，其获胜的概率为

其期望剩余为π＝ （γ（x）－c）［1－F（x）］n－1.

在对称均衡中，当x＝c时，期望剩余达到最大.

成本为r的供应商报价必为r，γ（r）＝r.

由此解微分方程 （4），得公开保留价时供应商报价函数

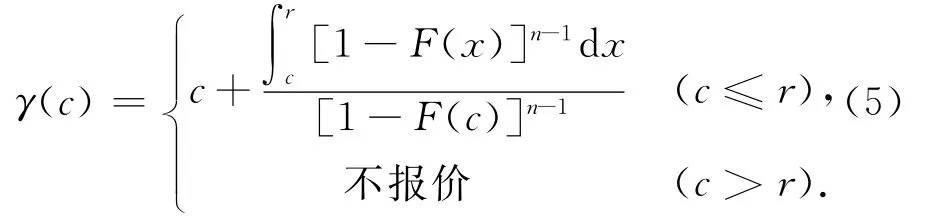
所以若公开保留价，当供应商选择报价时，报价都超出成本，超出部分为小于隐藏保留价时报价超出成本部分所以公开保留价时，供应商报价更低.

由于γ（c）为成本的增函数，所以成本越小报价越低.记c1为n个供应商中的最低成本，其密度为n［1－F（c）］n－1f（c），c∈ ［a，b］，其 密 度 函 数 为 n［1－F（c）］n－1f（c）.当c1＞r时，无人参与报价，采购商支付为0；当c1≤r时，成本最低的供应商通过报价γ（c1）赢得拍卖，采购商支付γ（c1）.所以采购商的期望支付

特别的，当成本c服从［a，b］上的均匀分布时，由式（5）可得，供应商报价函数

由式（6）可得，采购商期望支付

定理：当供应商的成本服从［a，b］上的均匀分布时，若采购商设定的保留价时，采购商应公开保留价；当时，隐藏保留价时采购商的期望采购成本更小，即EFC＜EFP.

因此，当采购商设定的保留价比较小时，应公开保留价以确保交易成功，而当保留价较大时，应隐藏保留价以降低采购成本.这个策略的直观解释是：当经济实力较差的时候，应该告诉卖方，己方可以接受的最高价格，而当有足够的经济实力时，应该隐藏这个信息，避免卖方乘机要价过高，从而减少采购成本.

3 第二价格密封拍卖的保留价分析

在第二价格拍卖中，由于胜者获得的支付不取决于自己的报价而是取决于次低报价，所以每个供应商都会尽可能报低价以增加其获胜概率，同时为了保证其收益非负，报价又必须不小于其成本.因此在第二价格密封拍卖中，不论保留价是公开还是隐藏，供应商报出成本价是一个弱占优策略.若次低价低于保留价，则按次低价获得支付.若次低价高于保留价，则按保留价获得支付.

设c2为供应商成本中的次低成本，c1为供应商成本中的最低成本，则c1，c2的联合分布为

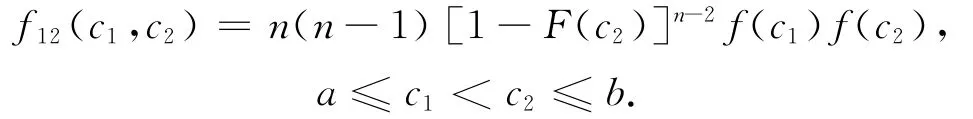
令Y表示采购商的支付，则

此时采购商的期望支付

特别的，当成本c服从［a，b］上的均匀分布时，由式（8）得，采购商期望支付

因此当保留价比较大时，采用隐藏保留价的第一价格密封拍卖的方式可降低采购商的采购成本.综上所述，对采购商而言，采用第一价格密封拍卖总是优于第二价格密封拍卖的.这也是实际采购拍卖中一般都采用第一价格拍卖的原因.

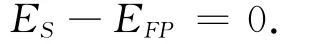
4 结束语

科学、合理、公平地制定拍卖和采购拍卖保留价是拍卖和采购活动中的重要环节，保留价方式的选取及定价策略是否恰当，直接关系到拍卖和采购能否顺利进行以及最终效率问题.本文研究了采购拍卖中采购商公开保留价与隐藏保留价时，供应商的报价策略与采购商的采购成本.结论表明：若供应商成本服从均匀分布时，当设定的保留价比较小，采购商采用公开保留价的第一密封价格拍卖或者第二价格拍卖的期望采购成本相等；当设定的保留价比较大时，应该采用隐藏保留价的第一密封价格拍卖.这个结果能为采购拍卖中供应商报价以及采购商采用合适的拍卖方式以及保留价策略提供一定的依据与参考价值.本文只考虑了成本是对称的，是均匀分布的情形，在供应商是非对称的情形和一般成本分布情形下保留价到底该公开还是保留，仍是值得后续研究的一个问题.

［1］Richard E W.On optimal reservation prices in auctions［J］.Management Science，1987，33（6）：763－770.

［2］Myerson R B.Optimal auction design［J］.Mathematics of Operation Research，1981，6：58－73.

［3］John G Riley，William F Samuelson.Optimal auction［J］.The American Economic Review，1981，71：381－392.

［4］Vincent D.Bidding off the wall：why reserve prices may be kept secret［J］.Journal of Economic Theory，1995，65：575－584.

［5］Vickrey William.Counter speculation，auctions，and competitive sealed tenders［J］.The Journal of finance，1961：9－37.

［6］Milgrom P R，Werber R J.A theory of auctions and competitive bidding［J］.Econometrica，1982，50：1 089－1 122.

［7］Eric S.Maskin，John G.Riley.Auction theory with private values［J］.The American Economic Review，1985，75（2）：150－155.

［8］Kathleen Carey.Reservation Price Announcement in Sealed Bid Auctions［J］.The Journal of Industrial Economics，1993，41（4）：421－429.

［9］Giovanni W P.Optimal bidding with announcement of the reservation price［J］.Rivista Di Politica Economica 2003，93（6）：117－130.

［10］杜 黎，胡奇英.网上分批拍卖中的保留价比较分析［J］.系统科学与数学，2002，7：343－354.

［11］维佳·克里斯纳.拍卖理论［M］.罗德明译.中国人民大学出版社，2010.

［12］徐雅卿，魏轶华，胡奇英.逆向拍卖保留价建模及数值分析［J］.西安电子科技大学学报（自然科学版），2007，34（3）：468－471.

［13］敬辉蓉，李传昭，陈尉纲.第一密封价格逆向拍卖机制博弈研究［J］.数学的实践与认识，2009，39（6）：38－44.