信息不对称下基于VMI模式的讨价还价模型
2011-10-24赵道致
安 彤 ,赵道致
(1.天津大学 管理学院,天津 300072;2.天津财经大学 数学系,天津300222)
信息不对称下基于VMI模式的讨价还价模型
安 彤1,2,赵道致1
(1.天津大学 管理学院,天津 300072;2.天津财经大学 数学系,天津300222)
VMI系统的引入需要采购商将市场和销售等信息与供应商共享,但采购商对供应商的成本结构却不一定了解,为此建立了基于VMI模式的单个供应商和单个采购商的讨价还价博弈模型,并假设采购商对供应商的成本结构具有不完全信息。通过讨价还价模型,得到了对于不同成本结构的供应商应给予不同的转移支付,最后算例分析验证了理论推导的结论。
信息不对称;VMI;讨价还价;转移支付
0 引言
“供应链管理是设计和保持一种良好的机制和模式,通过资源集成,借助合作企业的力量更好地发挥自身的核心优势,使自身和整个供应网络获得竞争优势的过程”[1]。因此,供应链伙伴间结成合作联盟,保持良好的合作对于链中的各方提高自身竞争力,快速形成自己独特的竞争优势具有战略作用。近几年来提出的供应商管理库存(VMI)正是一种建立在供应商—采购商伙伴关系基础上的供应链库存管理方法,其主要目标是更进一步提升供应链绩效。自从20世纪80年代晚期Wal-Mart在实践中较早地应用VMI模式并取得了很好成 效 后 ,Glaxosmithkline、Electrolux Italia、Nestle 和 Tesco、Boeing和Alcoa等也都陆续应用VMI模式取得了很好的效果。 Bernstein et al.(2006)[2]认为,将来供应链的上游供应商和下游集成商之间,在运营模式的选择上将越来越倾向于VMI。虽然有研究证明,VMI对提升供应链整体绩效有益,但这一合作模式能否实施取决于VMI模式给供应链上各方带来的经济效益。加之,在现实中供应链上下游之间信息不对称 (asymmetric information)的情况比比皆是,在双方实施VMI模式下,信息结构给高效率的激励机制设计造成很多困难,直接影响到VMI运营模式的效率和效果。
总之,近年来在供应链VMI模式协调优化方面的研究相对活跃,如 Yuliang Yao、Birendra K、Yan Dong[3-5]等都对这方面做了大量的研究,但是在目前问题比较突出的力量不对等供应链Pareto改善、供应商和采购商之间的讨价还价过程的研究还很少见,目前只有Eric Sucky(2005)[6]研究了基于JELS模型的讨价还价模型,并且上述文献在研究的过程中都假设供应链中的一方对另一方的成本结构具有完全信息。尽管从长期来看,信息共享可以使所有的参与者都获得好处,是供应链的主要利益[7],但供应链上下游企业的信息共享也可能产生一系列问题,所以在现实产业链中合作双方具有完全信息的情况是非常少见的,更多的是信息不对称的情况。 而目前只有 Corbett、de Groote[8]和 Eric Sucky(2006)[9]研究了单个供应商和单个采购商在信息不对称下的讨价还价过程。Corbett和de Groote假设采购商的订货成本是共同知识,供应商仅对采购商的库存持有成本不可见,并且假设采购商的库存持有成本是其订货成本和EOQ的隐函数,所以如果供应商知道采购商的订货成本和EOQ,供应商就能得到采购商的库存持有成本,因此信息不对称的问题被消除了。而Eric Sucky研究的是基于JELS模型的讨价还价模型,文中假设供应商对采购商的成本结构具有不完全信息。
本文把重点放在现在更为流行的VMI模式上,研究基于VMI合作模式的单个供应商和单个采购商组成的供应链系统。由于实施VMI后,采购商的库存委托给供应商管理,这就需要采购商向供应商提供真实的成本和销售信息,所以供应商对采购商的成本结构具有完全信息,但采购商对供应商的成本结构却不一定了解,为此本文建立了一个供应链上下游合作实施VMI的信息不对称的讨价还价模型,目的是针对不同成本结构的供应商,采购商向供应商提供不同的合作协议。
1 研究假设和符号表示
本文考虑由上游的一个产品供应商和下游的一个产品采购商组成的两层供应链结构。假设市场需求是确定的常数,供应商必须满足采购商的所有需求,不允许缺货。由于现在的市场多为买方市场,加上世界范围内的渠道连锁模式的兴起,下游比上游有着更强的议价能力,所以本文假设该系统中的采购商具有较强的议价能力,一旦和供应商就VMI合作谈判失败,在和供应商的交易过程中能强迫供应商接受满足采购商成本最优的订货策略。文中使用的数学符号如下:
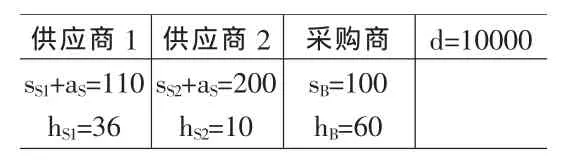
hB—采购商每年每单位产品的库存持有成本;sB—采购商每次订货成本;hS—供应商每年每单位产品的库存持有成本;sS—供应商每次订货成本;aS—供应商每次为采购商配送产品的成本;d—产品的年需求量。
2 实施VMI前后供应链的订货策略
实施VMI前,采购商与供应商的总成本分别为:

采购商根据EOQ策略决定的订货量为QB=(2SBd/hB)1/2,此时采购商的总成本为TCB(QB)=(2hBsBd)1/2。因为在大多数的现实产业链中,供应商在与采购商的博弈中往往处于劣势,所以供应商只能依据采购商给出的EOQ为采购商配送,所以将QB代入(2)中,得到此时供应商的总成本为:
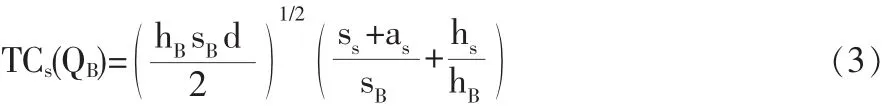
实施VMI后,采购商不再管理其库存系统,而改由供应商决定库存水平、订货量、提前期等。结果是,采购商将订货决策权转移给供应商的同时,将订货和库存持有成本也转移给供应商,此时供应商的总成本为:
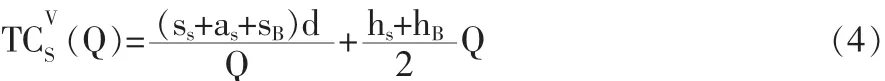
3 完全信息的讨价还价博弈
由上述分析可知,若[(1+γ)1/2-(1+φ)1/2]2,实施 VMI会使供应商的成本也下降,双方具有合作基础,交易时不必博弈,不涉及讨价还价,此时供应链达到完美协调;但若[(1+γ)1/2-(1+φ)1/2]2<2,虽然合作给采购商带来的直接益处显而易见,且已在实践中证明了,但却会使供应商的成本上升,在个人理性的前提下,供应商是不会接受合作策略的。虽然其他一些战略或管理因素,比如增强竞争优势,紧密采购商—供应商之间的关系或者合作或者简单的续存,也会在供应商是否采用VMI的决策中发挥作用,但底线是VMI最终能否为供应商节约成本或带来收入。所以,采购商为了激励供应商实施VMI合作策略,会向供应商提供一定的转移支付以弥补供应商由于选择合作策略而增加的成本,而转移支付的大小要依据上下游的讨价还价来确定,该博弈属于二人非零和博弈,博弈中双方的目标都是使自身成本最小。此时该讨价还价博弈可描述如下:
(1)一旦合作失败,采购商会迫使供应商接受满足采购商自身成本最小的EOQ策略QB;
(2)采购商向供应商提出VMI合作策略(包括转移支付),供应商只能选择接受或拒绝,无中间选择。在博弈的第一阶段采购商提出VMI合作策略,第二阶段供应商选择接受或拒绝,在供应商做出选择后,该博弈结束;
(3)采购商对供应商的成本函数具有完全信息;
采购商的目标是使其成本最小,从而得到以下成本最小化问题:
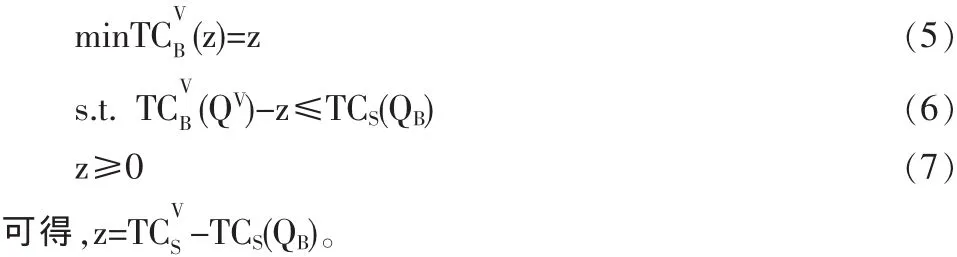
这说明,此时采购商向供应商提供的转移支付恰好弥补了供应商由于选择VMI而增加的成本,即无论供应商是否接受采购商提出的VMI合作策略,其成本都保持不变。而在现实产业链中随着全球竞争的日益加剧,现在的竞争已经不仅仅限于企业与企业之间的竞争,更扩大到其所在的链与链之间的竞争,供应商处于密切合作关系,增强其所在供应链的竞争优势的考虑,一般会接受该合作策略。同时,采购商为了激励供应商接受VMI策略,也可能会向供应商提供数额较小的额外激励。
4 信息不对称的讨价还价博弈
4.1 信息甄别模型
上述模型是在假定双方信息共享的基础上得到的,这在现实中是很难实现的。由于双方合作实施VMI,需要采购商将成本结构、产品需求等信息都与供应商分享,并为供应商提供一定的转移支付以补偿供应商同意合作而增加的成本,但采购商对供应商的信息并不十分了解,对于不同的供应商采购商会提供不同的转移支付,这就导致供应商可能会为了获得更多的转移支付而夸大其成本,那么采购商到底应该提供多少转移支付才能保证供应商参与合作的同时又避免自身因为合作而遭受损失。为了使供应商说实话,采购商就需要建立一个信息甄别模型,对于不同成本结构的供应商采购商提供不同的转移支付,每个转移支付对于每种类型的供应商都必须有吸引力,通过观察供应商接受的转移支付,从而确定供应商的真实成本结构[10]。假设双方均为风险中立,供应商有两种可能的成本结构类型,分别记为S1和S2,供应商为 S1和S2的概率分别为 p1和 p2,且 p1+p2=1(pi>0,i=1,2)。针对不同类型的供应商,采购商会提供不同的转移支付,以避免S1伪装成S2或S2伪装成S1,为此采购商要保证不同类型的供应商得到足够的转移支付。该博弈可描述如下:
(1)由于在现实产业链中采购商一般都占有强势地位,所以假设一旦合作失败,采购商会迫使供应商接受满足采购商自身成本最小的EOQ策略QB;
(2)采购商向供应商提供一个VMI合作策略(包括转移支付z≥0),采购商只能选择接受或拒绝,无中间选择。在博弈的第一阶段供应商提出VMI合作策略,第二阶段采购商选择接受或拒绝,在采购商做出选择后,该博弈结束;
(3)采购商对供应商的成本函数具有不完全信息,所以采购商最好为供应商提供一个转移支付组合(z1,z2),即对于不同类型的S1和S2分别提供不同的转移支付z1和z2;
采购商的目标是使其自身总成本的期望最小,从而得到以下成本最小化问题:
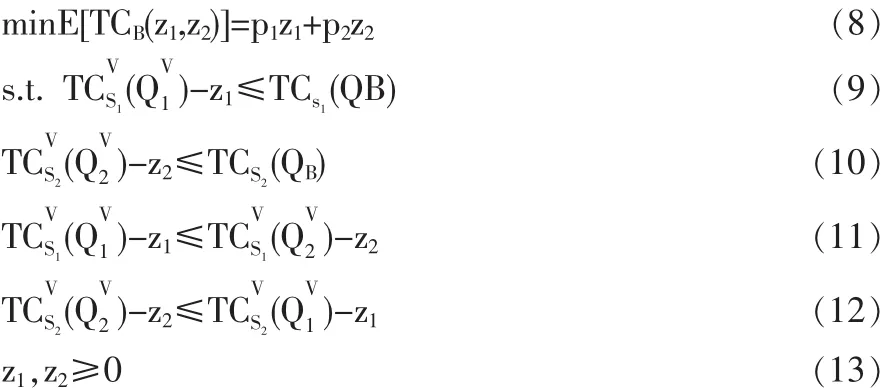
其中,约束条件(9)和(10)是参与约束,其确保供应商是个人理性的,即无论是哪种类型的供应商接受VMI后成本都不会增加;而约束条件(11)和(12)是激励相容约束,即无论是哪种类型的供应商都有积极性选择采购商希望他选择的转移支付。
4.2 讨价还价博弈模型的解
由于成本函数都是严格凸的,因此应用K-K-T条件:

由(14)+(15)得,p1+p2=λ1+λ2=1,所以 λ1=λ2=0 时不可行。由条件(14)可知,若 λ1=λ3=0,则 p1+λ4=0,又因为 p1,λ4≥0,所以 p1=λ4=0时不可行。 同理由条件(15)可知,λ2=λ4=0时也不可行。 当λ3,λ4>0 时,由条件(18)和(19)可得:

即z1=z2。因为本文假设S1、S2是不同类型的供应商,而采购商为不同类型的供应商会提供不同的转移支付,所以假设z1≠z2。
由于4个拉格朗日乘子都必须大于或等于0,所以拉格朗日乘子 λ1、λ2、λ3、λ4的组合共 16 种,由上面分析可知,其中有11种被排除,剩余5种如表1所示。
对于这5种可行的拉格朗日乘子组合,相应的可以得到以下 offer:
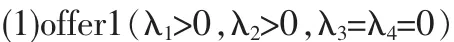
因为 λ1,λ2>0,所以由条件(16)和(17),可以得到转移支付:
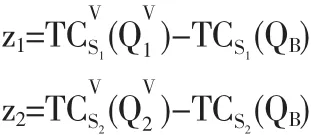
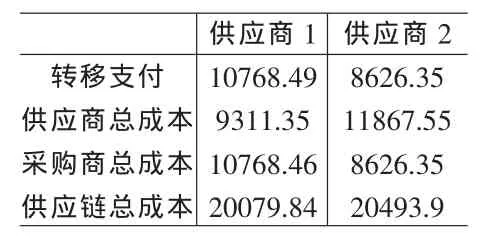
即无论是哪种类型的供应商,转移支付都恰好补偿了其因接受VMI而增加的成本。但offer1不能避免伪装会带来更大的成本节约,因此有可能出现S1伪装成S2或S2伪装成S1的情形,以获得伪装而节约的成本如果z1>z2,S1获得的转移支付大,S1当然不愿意伪装。但此时S2是否会伪装成S1,要视采购商为S1提供的转移支付多少而定。如果采购商为S1提供的转移支付大大超过S2的伪装成本,S2有利可图,那么S2会伪装成S1以获得额外的伪装所带来的成本节约。反之,若z1 那么offer1就满足所有K-K-T条件,offer1既是可行也是最优的。 上面的两个不等式说明,当S1与S2的成本结构差别不大时,offer1最优。此时无论为S1还是为S2提供的转移支付都与信息对称时相同,这是因为S1与S2的成本结构差别不大,即使供应商伪装,获得的额外成本节约也不会很大,但却降低了供应链整体的绩效,供应商处于密切合作关系,增强供应链竞争力角度考虑,一般不会冒着破坏双方长期合作关系的风险而选择伪装。 因为 λ1,λ4>0,所以由条件(16)和(19)可得: 与对称信息相比,采购商增加了为S2提供的转移支付,目的就是鼓励 S2不说谎。 若 z1、z2还满足条件(17)、(18),即 第一个不等式说明当S1与S2的成本结构差别较大,且当采购商在实施VMI前决定的订货量更接近于供应商S1在合作前依其自身成本最小决定的订货量时,offer2最优。由于转移支付 z1、z2满足即 S2伪装成S1后的成本与不伪装的成本相同,所以S2不会伪装。这是因为,虽然采购商为S1提供的转移支付较多(z2 因为 λ1,λ3>0,所以由条件(17)和(18)可得: 与对称信息相比,采购商增加了为S1提供的转移支付,目的就是鼓励 S1不说谎。 若 z1、z2还满足条件(16)、(19),即 第一个不等式说明,当S1与S2的成本结构差别较大,且当采购商在实施VMI前决定的订货量更接近于供应商S2在合作前依其自身成本最小决定的订货量时,offer3最优。与offer2的分析类似,由于转移支付z1、z2满足即S1伪装成S2后的成本与不伪装的成本相同,所以S1不会伪装。这是因为,虽然采购商为S1提供的转移支付较多(z1 考虑表2中所示算例。在对称信息下,供应商和采购商的讨价还价结果如表3所示,采购商为S1提供的转移支付为10768.49,为S2提供的转移支付为8626.35。因为采购商为S1提供的转移支付较多,所以S2可能会伪装成S1以获得更多的转移支付,这就会给采购商带来更大的成本负担,为了避免这种情况的出现,采购商需要建立信息甄别模型。在该算例中,通过讨价还价可以得到,在信息不对称下采购商为供应商提供offer 2是最优的,讨价还价的结果如表4所示,采购商为S1提供的转移支付为10768.49,为S2提供的转移支付为9598.99。 从表3和表4中可看出,即使在信息不对称的情况下,采购商为S1提供的转移支付仍比S2多,此时采购商为S1提供的转移支付并没有改变,但却增加了为S2提供的转移支付,目的就是鼓励S2不说谎。虽然采购商因此支付了更多的转移支付,但同时也避免了因为供应商说谎而造成的更大成本负担。由表3和表4可知,在对称信息下,S2的总成本为11867.55,采购商的总成本为8626.35,供应链的总成本为20493.9;在不对称信息下,S2的期望成本为 10894.86,采购商的期望成本为10064.79,供应链的总成本为20959.65。显然,在不对称信息下S2的成本更低、采购商和供应链的成本更高。可见伪装虽然对供应商有利,但却会给采购商甚至整个供应链带来额外的成本负担。虽然信息共享不充分会降低整个供应链的绩效,但供应商处于个人理性却往往会选择伪装,这也是在现实产业链中常常会出现该现象的原因,而本文提出的讨价还价模型能够使这种信息共享不充分所造成的供应链损失降至最低。 本文通过建立一个基于VMI模式的单个供应商与单个采购商之间的信息不对称的讨价还价模型,研究了VMI对整合的供应链战略的作用以及它对参与双方的吸引力,为了更贴近大多数的现实产业链,本文假设采购商在与供应商的讨价还价中占有优势地位。研究表明如果采购商能估计供应商的可能成本结构类型,那么采购商就可以利用信息甄别函数得到的结果作为签订VMI合同时的参考。 本文主要从成本节约角度研究了VMI对参与双方的吸引力。从长期来看,当采购商和供应商都调整生产、配送和营销并利用这种成本较低的库存系统后,最终的销售量以及采购量都很可能上升,就像Proctor and Gamble(Nolan 1997)在物流实践中观察到的一样。而其他战略上的益处,比如与采购商的长期伙伴关系、某些成本部分的减少都可能使得VMI项目对供应商具有吸引力,所以在现实中,即使采购商支付的转移支付不足以弥补供应商接管采购商库存而增加的成本,供应商从长远利益考虑也有可能接受短期来看并不吸引人的VMI合作策略。总之,本文的研究说明有兴趣采用VMI的企业除了应该着重分析参与双方库存系统的成本构成和显著差别外,还应重视转移支付在合作企业之间所起到的重要作用。 表1 拉格朗日乘子的可行组合 表2 供应商和采购商的成本结构 表3 对称信息下的讨价还价结果 表4 不对称信息下的讨价还价结果 [1]Zhao D Z,Fang M.The Key of Network Manufacturing:Intergrating Material,Information,Capital and Knowledge Flows[C].The Proceedings of the 7th Annual International Manufacturing Symposium(ISBN1-902546-23-7),Cambridge,UK,2002. [2]Bernstein F,Chen F,Federgruen A.Coordinating Supply Chains with Simple Pricing Schemes:The Role of Vendor-Managed Inventories[J].Management Science,2006,52. [3]Yao Y L,Philip T E,Martin E D.Supply Chain Integration in Vendor-managed Inventory[J].Decision Support Systems,2007,43. [4]Birendra K,Mishra,Srinivasan R.Retailer-vs.Vendor-Managed Inventory and Brand Competition[J].Management Science,2004,50. [5]Yan D,Xu K F.A Supply Model of Vendor Managed Inventory[J].Transportation Research Part E,2002,38. [6]Eric S.Inventory Management in Supply Chains:A Bargaining Problem[J].International Journal of Production Economics,2005,93. [7]彭剑.供应链中信息共享问题研究综述[J].物流技术,2006,6(1). [8]Corbett C J,Groote X D.A Supplier’s Optimal Quantity Discount Policy under Asymmetric Information[J].Management Science,2000,46(3). [9]Eric S.A Bargaining Model with Asymmetric Information for a Single Supplier-single Buyer Problem[J].Europeanl Journal of Operational Research,2006,171. [10]Illing G.Private Information as Transaction Costs:Thee Coase Theorem Revisited[J].Journal of Institutional and Theotetical E-conomics,1992,148. [11]Bernstein F,Federgruen A.DynamicInventory and Pricing Models for Competing Retailers[J].Naval Research Logistics,2004,51. [12]Bernstein F,Federgruen A.Decentralized Supply Chains with Competing Retailers under Demand Uncertainty[J].Management Science,2005,51(1). [13]Cheung K,Lee H.The Inventory Benefit of Shipment Coordination and Stock Rebalancing in a Supply Chain[J].Marketing Science,2002,48(2). (责任编辑/易永生) F273.7 A 1002-6487(2011)03-0058-04 国家自然科学基金资助项目(70771073) 安 彤(1980-),女,辽宁辽阳人,博士研究生,讲师,研究方向:物流与供应链管理。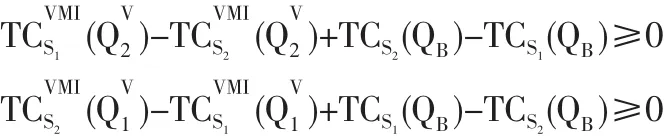
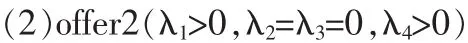
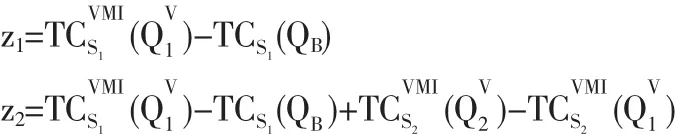
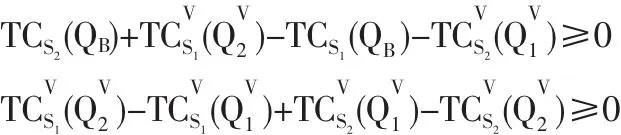



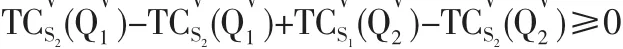
4.3 算例
5 结论