基于模拟退火原理的二元光学元件设计改进GS算法＊

李 淼 唐建波 刘 俭

（1.海军驻431厂军事代表室 葫芦岛 125004）（2.哈尔滨工业大学超精密光电仪器工程研究所 哈尔滨 150080）

1 引言

二元光学器件（Binary Optical Element，BOE）是利用计算机辅助设计而成的微浮雕结构衍射光学器件[1]，在光束的整形和变换[2]、光束耦合、聚焦、分束[3]、消除光学系统色差[4]及超分辨滤波器设计[5]等方面有广泛的应用，二元光学元件计算机辅助设计已成为当今光学领域的一大研究热点。通常的BOE设计算法大致可以分为两类：基于线性变换方法如 GS算法[6]、杨－顾算法（Y－G算法）[7]等，基于搜索极值的优化法如模拟退火算法（Simulated Annealing，SA算法）[8]、遗传算法（GA 算法）[9]等，以及如参考文献[1、3、10、13]等所述的众多改进算法。BOE设计具有结构复杂、计算量大等特点，实现计算量小、收敛快、对初始值选取敏感性低、抗局部极值能力强、易于求得问题的全局最优解是BOE计算机优化设计算法研究的重要任务[1]。

传统的GS算法收敛速度快，但其存在着对初始值敏感、易陷入局部极值等问题[10]；SA算法以一定的概率接受使评价函数变差的自变量取值，从而使算法能跳出局部极值，但其实质是以足够高的初始温度，缓慢的退火速度，大量的迭代次数及同一温度下足够多的扰动次数为保证的，从而导致了收敛效率十分低下，算法的计算量非常大[12]。本文在深入分析了模拟退火原理和传统GS算法优点的基础上，结合模拟退火原理抗局部极值的思想和GS算法收敛目标明确、效率高的特点，提出了基于模拟退火原理的改进GS算法，并用改进算法和传统GS算法对不同振幅分布目标进行了计算机仿真实验。

2 BOE设计理论及基本设计算法

2.1 BOE设计理论

BOE设计理论基于图1所示的傅里叶光学变换系统，输入面P1和输出面P2分别位于傅里叶透镜的前焦面和后焦面，二元光学元件BOE置于P1面上，单色平面波fipt（x，y）垂直入射到BOE平面，经过BOE的衍射作用和透镜L的傅里叶变换，在P2面得到所需的光场振幅分布Ftgt（ξ，η）。

BOE设计的实质是[11]：入射光波透过BOE后波前相位受到调制，然后经过透镜的傅里叶变换作用在输出平面上呈现出某种光强分布，并且BOE的相位分布与输出平面上的光强分布是一一对应的，即一种相位分布对应一种输出平面上的光强分布。这个过程在物理上是正过程，而BOE的设计正好是这个过程的逆过程，即从任意给定的输出平面上的目标分布函数Ftgt（ξ，η）和入射光波分布函数fipt（x，y）去求解引起此光强分布的BOE的相位分布函数φ（x，y），使最终求得的相位分布函数φ（x，y）、入射光波分布函数fipt（x，y）及目标振幅分布函数Ftgt（ξ，η）满足公式：

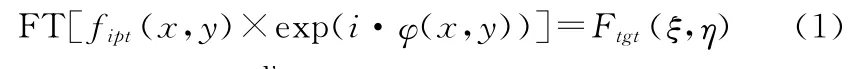
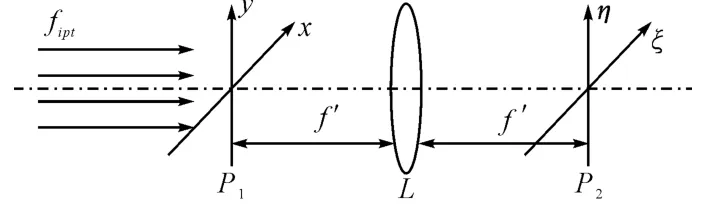
图1 傅里叶光学变换系统

2.2 模拟退火原理

模拟退火算法（SA）作为局部搜索算法的扩展，其核心思想是在每一次修改模型的过程中，在先前最优状态的邻域内随机产生一个新的状态模型，然后以一定的概率选择邻域中评价函数更好的状态，这种接受新模型的方式使其成为一种全局最优算法[3]。模拟退火原理基本思想描述如下[12]：

1）设初始状态i为当前状态，该状态的能量为Ei，然后对该状态做随机微扰，得到一个新状态j，新状态的能量为Ej；

2）如果Ej＜Ei，则取状态j为当前状态；如果Ej＞Ei，则考虑到热运动的影响，状态j是否为重要状态根据固体处于该状态的概率来判断，若状态i和j的概率比值exp[（Ei－Ej）／（kb·T）]＞r，r为区间[0，1]上的随机数，则以状态j取代状态i成为当前状态，否则仍以状态i为当前状态，再重复以上新状态的产生过程；

3）在大量固体状态变换后，系统趋于能量较低的平衡状态，固体状态的概率分布趋于Boltzm－ann概率分布。

模拟退火原理的实质是在以100%的概率接受使评价函数变好的邻域扰动自变量取值的同时以exp（（Ei－Ej）／T）＞rand（1）的概率接受使评价函数变坏的自变量改变，使其能跳出局部极值，模拟退火算法应用于二元光学计算机辅助设计时计算量很大，效率十分低下，这也是一直影响其真正走向实用的主要障碍[1]。

2.3 GS算法

GS算法应用于二元光学元件计算机辅助设计的基本思路是[6]：以初始相位和给定的入射光场分布，通过做正向傅里叶变换，得到输出平面光场分布；在输出平面用期望的光场振幅分布取代正向傅里叶变换得到的光场振幅分布，并且保持相位不变；然后做逆向傅里叶变换，得到输入平面光场分布；在输入平面用给定的光场振幅分布取代逆向傅里叶变换得到的振幅分布，并且保持相位不变；接着再次做正向傅里叶变换，如此循环下去，直到得到满意结果或达到足够多的循环次数为止。

GS算法是一种收敛速度很快的算法，但值得注意的是GS算法对初始参数很敏感，容易陷入局部极值[10]。

3 改进算法原理

GS算法是反复采用正傅里叶变换和逆傅里叶变换逐步收敛到目标函数的线性变换算法，具有目标明确、计算量小、收敛速度很快的特点，但用这种算法搜索函数的极小值时，如果函数在其定义域范围内单调性不好，波形起伏频繁，则收敛的效果就不会很好，不能跳出局部最优解，收敛结果严重依赖于初始相位的选取[10]；模拟退火算法的核心思想是逐步的退火计划和以一定的概率接受恶化解以跳出局部最优解，但其计算量大，效率低下[1]。针对这两种算法应用于二元光学元件设计的缺点，人们提出了多种改进算法，如参考文献[1、3、10、13]所述。本文基于对模拟退火原理及GS算法特点的分析，设计了基于模拟退火原理的改进GS算法，并通过仿真实验验证了改进算法的优越性，算法设计如下：

1）对初始温度T0、目标温度Tend、降温速度dT、回火升温阈值温度Tlow、初始位相解φ0（x，y）等初始化。

2）对位相解φbest（x，y）做邻域扰动，得到位相新解φnew（x，y）：

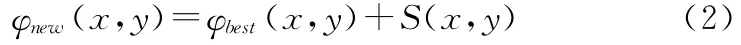
其中S（x，y）为邻域扰动因子，当T＞Tlow时，采用指数递减因子Se（x，y）：

其中k为迭代次数，a、b为自设系数；

当T≤Tlow时，采用依赖于温度的似Cauchy递减因子Sc（x，y）：

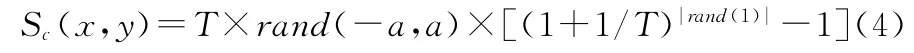
其中T为当前温度。

3）以位相新解φnew（x，y）和给定的入射光场分布fipt（x，y）做正傅里叶变换得到输出面上的复振幅分布F（ξ，η）：

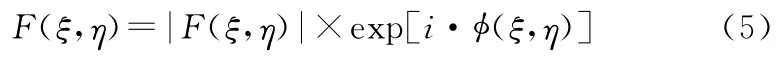
由｜F（ξ，η）｜计算评价函数SSEnew和评价函数改变量ΔSSE：

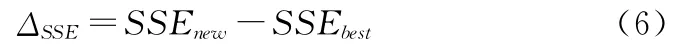
4）如果评价函数改变量ΔSSE满足条件：

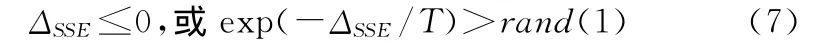
（当T≤Tlow时取下降速度更快的T′，以保证最后只接受使评价函数变好的结果）

则以目标振幅分布和在步骤（3）中得到的位相解φ进行傅里叶逆变换得到f（x，y）：

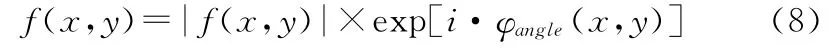
并接受φangle（x，y）为φbest（x，y），SSEnew为SSEbest。

5）否则结束本次循环，φbest（x，y）、SSEbest保持不变，重复执行2）～5），直到满足当前温度下内循环条件。

6）降温，进行下一组迭代直到温度下降到目标温度Tend。

在步骤2）中当T≤Tlow时算法进行了回火升温处理并且改变了邻域扰动方式，依赖于温度的似Cauchy分布产生新邻域的优点是：在高温情况下搜索范围大，在低温时搜索仅在当前模型附近，即具有从高温到低温扰动范围逐步平滑下降的特性，从而使其易于迅速跳出局部极值，并能很好保持搜索到的最优解[12]，通过这一改进可以使模型具有再次跳出局部极值的机会，提高了模型的全局寻优能力，并且逐步降低接受恶化解的可能性，使模型最终能很好保持搜索到的最优解；在步骤4）中改进算法进行有选择的傅里叶逆变换，即当满足式（7）所示条件时进行傅里叶逆变换，减少了运算时间，提高了迭代效率。基于模拟退火原理的改进GS算法流程如图2所示。

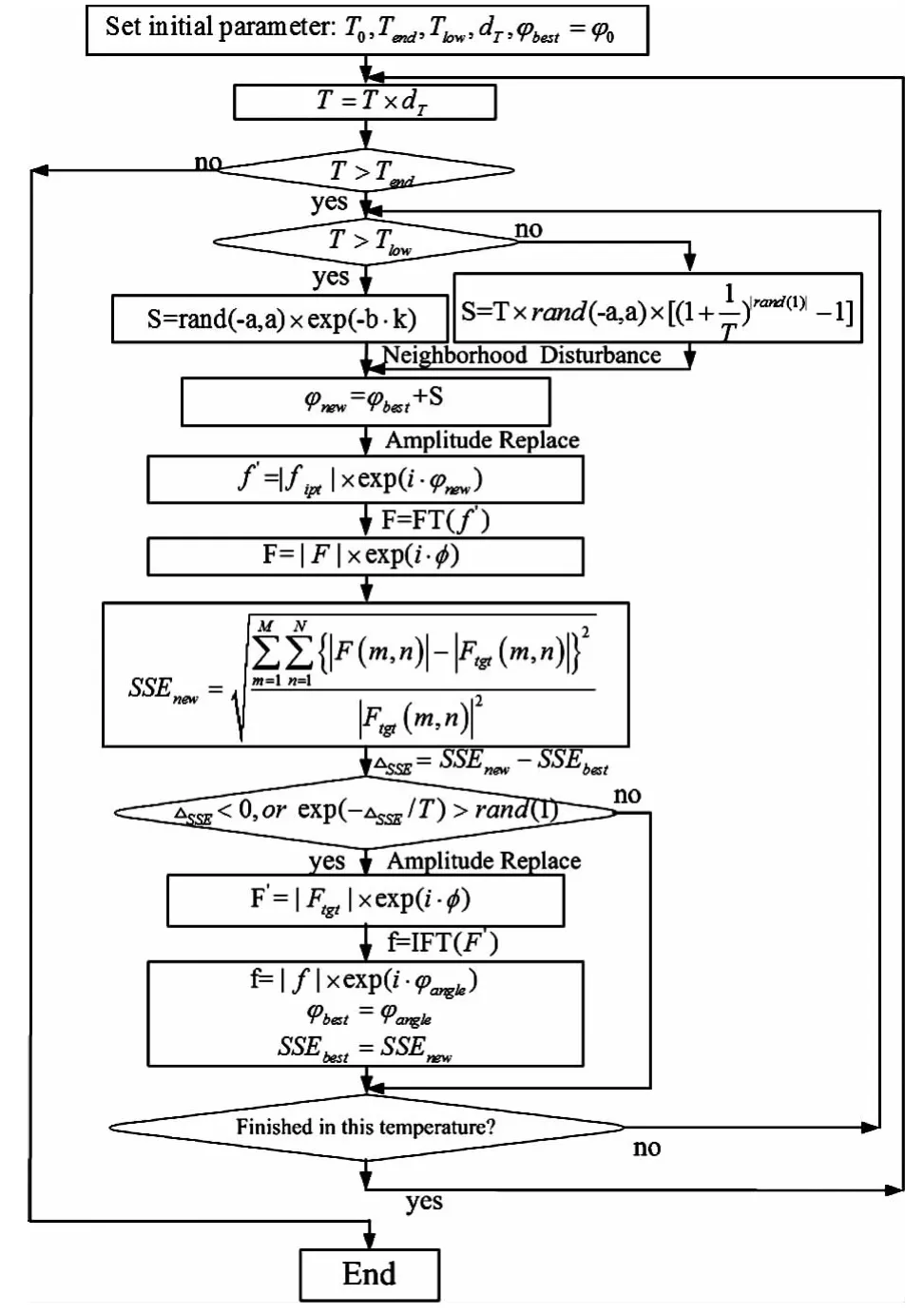
图2 改进GS算法流程图

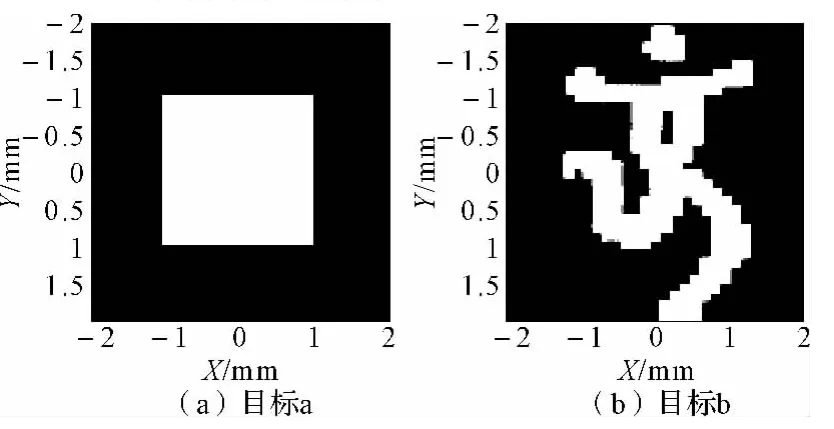
图3 目标振幅分布

通过对目标a所示图形进行仿真实验可以验证算法对呈中心对称分布图形的设计性能，对目标b所示图形进行仿真实验则可验证算法对任意分布图形的设计性能。

均方误差SSE和拟合系数η是衡量再现图样与目标图样差异的主要指标，能够反映出再现图样的均匀性以及再现图样与目标图样的接近程度，在实际设计计算中，一般将均方误差SSE或拟合系数η作为优化设计算法的目标函数[10]，本文采用均方误差SSE作为评价函数，拟合系数η作为辅助评价手段。

传统的模拟退火算法采用对BOE元件各个相位单元进行逐个寻优，这是导致SA算法效率低下的一个重要原因[13]，本文所探讨的改进算法采用的是对整个BOE元件的相位面进行邻域扰动寻优，其核心思想是以GS迭代为基本框架，但在每一次GS迭代中都采用了模拟退火原理思想，在保证算法收敛效率的同时增加了算法的抗局部极值能力，能更好的全局寻优，并且通过引入判断条件减少了进行傅里叶逆变换的次数，收敛效率相对于GS算法得到了进一步提高。

4 仿真实验与分析

本文采用图1所示的傅里叶变换光路进行仿真实验，设定入射高斯光束波长632.8nm，束腰半径1.5mm，BOE元件边长为x＝y＝5mm，输入与输出面采样点数均为128×128。

为了验证改进算法对二元光学元件计算机辅助设计的有效性，目标图形采用如图3（a）所示呈中心对称分布的方形光斑，其中方形光斑边长为2mm×2mm，以及如图3（b）所示模拟任意形状的北京奥运会会徽图案：

φ（x，y）即为所求二元光学元件的位相分布。

通过取不同的初始相位可以判断算法对初始相位的敏感性，因此当以图3（a）为目标分布时，初始相位分别取以下四种情况：

1）φ0（x，y）取128×128维全0矩阵；

2）φ0（x，y）取128×128维全1矩阵；

3）φ0（x，y）取通过目标振幅分布Ftgt（ξ，η）傅里叶逆变换获得的相位值；

4）φ0（x，y）取元素为[－π，π]之间随机值的128×128维矩阵；

用GS算法和改进算法在以上四种情况下取相同的初始相位得到的仿真结果如表1所示，计算时间是在计算机CPU为AMD Athlon64，主频2.31GHZ下得到的。

由表1可以看出在以上四种初始相位情况下，改进算法相对于GS算法均方误差SSE平均减小了14.83%，拟合系数η平均提高了0.04%，迭代4000次所用时间平均减少了15.63%，证明改进算法相对于传统GS算法具有计算量小、收敛快、全局寻优能力强的特点；同时我们也发现当初始相位取前三种情况时，在每一种情况下GS算法迭代4000次都得到相同的结果，说明GS算法在很大程度上受制于初始相位的选取，抗局部极值能力弱；而改进算法因为采用了模拟退火原理的思想，通过邻域扰动及以一定概率接受使评价函数变坏的结果，降低了对初始值选取的敏感性，提高了全局寻优能力。

其中，Ftgt（ξ，η）为目标复振幅分布，F（ξ，η）为入射波光束垂直入射到BOE后经过透镜的傅里叶变换在成像面上得到的复振幅分布：

表1 不同初始相位下传统GS算法和改进GS算法仿真结果

图4（a）所示为采用随机初始相位时改进算法和GS算法的评价函数曲线图，由图可知GS算法在迭代2453次时达到局部极值，其后的迭代结果没有明显的改进，并且最终不能保持搜索到的最优解；改进算法在第一阶段收敛到局部极值后，经过再次升温扰动，模型具有了跳出局部极值的能力，经过第二阶段的扰动寻优后，取得了更好的寻优结果，并且在其后的迭代过程中逐步降低接受评价函数变坏的概率直到只接受使评价函数变好的扰动，使得改进算法的寻优能力得到了明显的提高。

图4（b）所示为采用改进算法和GS算法取第四种初始相位情况下进行25000次迭代获得的评价函数曲线图，仿真结果显示：GS算法获得的最小均方误差SSE＝4.5%，最优拟合系数η＝97.77%，耗时755.2s；改进算法获得的最小均方误差SSE＝3.68%，最优拟合系数η＝97.82%，耗时611.59s，并且自第二次扰动后评价函数值一直优于GS算法并在迭代结束时获得最优解。进一步验证了改进算法随着迭代次数的增加可进一步搜索全局最优解，具有很强的全局寻优能力，而GS算法已陷入局部极值不能继续寻优。

图4 GS算法和改进算法仿真实验评价函数曲线图

图5（a）、（b）分别为在第4种情况下取相同的初始相位时GS算法和改进算法迭代4000次仿真得到的输出面振幅分布截面图，由图可知改进算法获得的结果中心方形光束部分能量更集中，并且方形光束之外区域光场分布更少，所得结果更接近目标振幅分布。

当以图3（b）所示图形（北京奥运会会徽图案）为目标振幅分布时，采用改进算法及GS算法取相同的随机初始相位分别迭代4000次得到的评价函数曲线如图6所示。

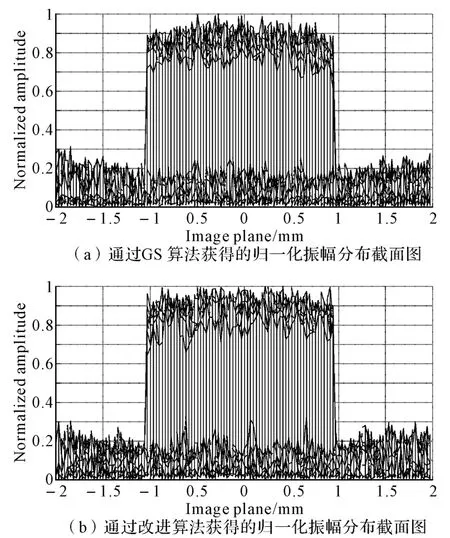
图5 输出面归一化振幅分布截面图

图6 GS算法和改进算法仿真实验评价函数曲线图

仿真结果显示：GS算法获得的最小均方误差SSE＝6.577%，最优拟合系数η＝98.04%，耗时131.3s；改进算法获得的最小均方误差SSE＝5.739%，最优拟合系数η＝98.08%，耗时115.4s，并且自第二次扰动后评价函数值一直优于GS算法并在迭代结束时获得最优解；证明改进算法对GS算法的优越性同样适用于对任意不对称分布目标图形的二元光学元件计算机辅助设计。

灰度直方图反映了图像中各个灰度级与该灰度级像素出现的频率之间的关系，明亮图像的灰度直方图倾向于灰度级高的一侧，对比度高的图像直方图覆盖的灰度级很宽而且像素分布不均匀，集中分布在高灰度级和低灰度级上[14]，因此通过灰度直方图可以评断图像的明亮程度及对比度。图3（b）具有对比度高、目标图像明亮的特点，因此若仿真图形的直方图覆盖的灰度级宽、并且趋近于灰度级高的一侧，则获得的效果更好。图7（a）、（b）分别为GS算法和改进算法仿真得到的输出面图形的灰度直方图，由图可知GS算法获得的直方图明暗波峰覆盖范围为182、明亮成分中心灰度级为196，而改进算法获得的直方图明暗波峰覆盖范围为194、明亮成分中心灰度级为208，说明改进算法获得的图形的直方图覆盖的灰度级宽、并且趋近于灰度级高的一侧，因此改进算法的优化设计效果更好。

图7 输出面图像灰度直方图

图8（a）、（b）分别为GS算法和改进算法仿真得到的效果图。

图8 输出面振幅分布

5 结语

改进算法以GS迭代为基本框架，在每一次迭代过程中又引入了模拟退火的思想，首先确保了收敛的速度，具有很高的效率，然后对每一次迭代的自变量都引入了邻域扰动，并且以一定的概率接收恶化解，使算法具有跳出局部最优解的能力，在温度下降到一定阈值后进行升温处理并且改变邻域扰动因子，给模型再次跳出局部极值的机会，在很大程度上保证了全局寻优。本文通过采用两种不同的目标图像进行仿真，验证了改进算法的优越性，其运行效率高，全局寻优能力强，并且降低了对位相初值的敏感性，能对任意目标图像进行计算机仿真设计，是进行二元光学元件计算机辅助设计的有效算法，在二元光学计算机优化设计中具有很好的应用前景。

[1]康果果，谢景辉，莫晓丽，等.用改进的两步模拟退火法进行二元光学元件的设计[J].光子学报，2008，37（7）：1416－1419.

[2]谢梦，曾晓东，安毓英.大功率半导体激光器二元光学消像散器件设计[J].红外与激光工程，2007，36（1）：102－105.

[3]尹霄丽，余重秀.用改进的模拟退火算法设计二元光学阵列器件[J].光电子·激光，2001，12（2）：154－157.

[4]孙强，唐同斌，董国才，等.红外场景产生器折射／衍射准直光学系统设计[J].红外与激光工程，2007，36（6）：881－883.

[5]Jian Liu，Jiubin Tan，Yanchao Wang.Synthetic Complex Super－resolving Pupil Filter Based on Double－beam Phase Modulation[J].Applied Optics，2008，47（21）：3803－3807.

[6]Gerchberg RW，Saxton WO.A practical algorithm for the determination of phase from image and diffraction plane pictures[J].Optic，1972，35：237－246.

[7]杨国祯，顾本源，董碧珍.衍射光学元件的设计新方法[C]／／中国光学学会95年会特邀报告专辑，1994，39（5）：371－376.

[8]KIRKPATRICK S，GEL ATT C D，VECCHI M P.Optimization by simulated annealing[J].Science，1983，220（4598）：671－680.

[9]Gabreal Cormier，Roger Boudreau，Sylvain Theriault.Real－codid genetic algorithm for Bragg grating parameter synthesis[J].Opt.Soc.Am.B，2001，18（12）：1771－1776.

[10]邹杰宇，卢亚雄，黄子强，等.基于改进GS算法的衍射光学光束整形元件的设计[J].红外与激光工程，2006，35（S）：48－52.

[11]孔令彬，叶敦范，易新建，等.多相位256×256衍射微透镜的设计及其光学性能研究[J].红外与激光工程，2002，31（3）：253－256.

[12]陈华根，吴健生，王家林，等.模拟退火算法机理研究[J].同济大学学报（自然版），2006，34（18）：1121－1125.

[13]谢敬辉，刘锡宇.基于DPDV算法的二元光学元件设计[J].光学技术，2000，26（3）：225－227.

[14]Rafael C.Gonzalez，Richard E.Woods.数字图像处理[M].阮秋琦，阮宇智，译.北京：电子工业出版社，2008，11.