运动单站定位与多站测向定位的统一理论模型
2013-08-10石荣,阎剑,张聪
石 荣,阎 剑,张 聪
(电子信息控制国家重点实验室,成都610036)
将式(7)与式(8)代入式(6)可得:
式中:
0 引 言
根据观测站的数目可以将无源定位问题划分为两大类:一类是单站无源定位;另一类是多站无源定位。一般情况下,在单站无源定位中,都要求观测站与目标之间存在相对运动;而多站无源定位则无此要求。
在运动单站对固定目标的无源定位中,目前普遍采用在辐射源来波方向测量的基础上,结合基于切向运动的测距来实现定位。这一单站定位方法所需要测量的物理量主要包括2个参数:来波方向和来波方向的角度变化率,而这2个参数的常用测量方法都是通过干涉仪来完成的。根据干涉仪测向计算公式,通道间的相位差为:

式中:L为干涉仪2个接收天线之间的间距;λ为电磁波波长;θ为来波方向角。
由此可见:干涉仪通道间的相位差信息直接对应了辐射源的来波方向角,而相位差变化率信息也就反映了来波方向角的角度变化率,因为从数学模型上看,后者是前者对时间求导的结果,即:

在获得θ与˙θ的基础上,结合运动平台的速度参数,便可计算出观测站与辐射源之间的距离r,从而实现单站定位[1-2]。
在多站无源定位方法中有时差、频差和测向交叉等体制。而最常用的是测向交叉定位,即各个观测站在对辐射源来波方向进行测向的基础上,通过方向信息的处理与融合得到辐射源的位置[3],这样多站之间的站间协同要求程度最低,应用方便。
如前所述,单站定位与多站定位在理论模型与处理流程上基本相互独立,各自形成了2套处理方法,而且在系统上几乎也是分离设计,造成了无源定位系统应用上的隔阂与冗余配置。针对这一问题,本文从另外一个视角出发,利用多站测向交叉定位理论对基于切向运动测距的单站定位方法进行了分析与解释,在时间尺度上通过短时观测特性,从多站测向交叉定位理论模型自然过渡到了基于切向运动测距的单站定位理论模型;在数据处理上,通过最小二乘来展示了2种方法的统一性,从而揭示了2种定位方法之间的相互联系,建立了基于切向运动测距的单站定位与多站测向交叉定位的统一理论模型,并通过仿真进行了验证。
1 基于切向运动测距的单站定位理论模型
到目前为止,大量的文献对基于切向运动的单站定位体制的技术原理、测量方法、数据处理流程等各个方面进行了全面的论述[4-8],虽然从理论上讲,基于切向运动测距的单站定位具有瞬时定位能力,但是在实际应用中,采用该方法进行定位时都有一个逐渐收敛的持续时段过程,然后才能达到一定的定位精度。
基于切向运动测距的单站定位理论主要有2种表述方式:一种是基于运动学的表述;另一种是基于几何学的表述。此处主要从运动学的角度在二维平面条件下简要概述[2]。
根据物理学中的匀速圆周运动相关定律,有下式成立:

式中:vT为运动质点的线速度,其方向始终保持与圆周相切,此处的线速度相当于切向速度;ω为角速度。
如果将运动质点与圆心之间的连线和固定参考方向形成的夹角记为θ,那么有即ω也等于构造出的夹角的角度变化率,r为运动质点与圆心之间的距离,利用式(3)可求得距离r为:

式(4)即是在运动学中利用切向速度和角度变化率来进行测距的理论计算公式。
在工程应用中,通常情况下运动单站采用干涉仪对来波方向进行测向,从而获得角度测量值θ序列,并同时获得角度变化率的测量值˙θ,然后在与该来波方向相垂直的方向上,利用传感器获得运动平台的切向速度测量值vT,通过式(4)便可计算得到观测站与目标之间的距离值r,从而在以运动单站为原点的本地极坐标系下得到辐射源的定位位置为(r,θ)。由于上述方法中采用了干涉仪测向和干涉仪通道间的相位差变化率测量,所以该单站定位方法在工程上也被称为“基于干涉仪相位差变化率测量的单站定位”。
2 多站测向交叉定位理论模型
多站测向交叉定位在部分文献中也被称为“三角定位”,其基本原理可以从双站测向交叉扩展至多站测向交叉,所以下面以二维平面条件下的双站测向交叉定位为基础进行理论分析。2个观测站与固定目标点之间的位置如图1所示。2个观测站之间的距离记为S,这2个观测站也可看成是由1个观测站在ΔT的时间内以速度v0运动了一段距离S=v0·ΔT的再次测量,且2个观测站相对于同一参考方向测量得到的来波方位角分别为θ1和θ2。

图1 双站测向交叉定位示意图
图1中记观察站O1与目标T之间的距离为r,根据图1中的几何关系有下式成立:

由式(5)可知,在运动时间ΔT已知且来波方向角θ1、θ2和运动速度v0可由相关传感器测量得到的条件下,由式(5)可计算出在以观测站O1为原点的本地极坐标系下辐射源的位置(r,θ1)。
在多站测向交叉定位中,可以得到多个类似于式(5)的测量等式,然后通过各种形式最小二乘方法来得到最终融合后的辐射源定位值。
3 单站定位与多站定位之间的统一理论模型
3.1 两种定位模型在时间尺度上的统一性分析
在前面的双站测向交叉定位中,记Δθ=θ2-θ1,于是可将式(5)重新整理如下:

如果将双站测向交叉定位看成由1个观测站经过ΔT时间的运动后,在2个不同位置上的观测结果,在ΔT非常小(即ΔT趋近于0)时,θ1与θ2趋近于相等,记为:也趋近于零,即,在此时这一双站测向交叉定位过程也就演变成了运动单站对固定目标的定位过程,且有如下关系式成立:

将式(7)与式(8)代入式(6)可得:

式中:sinθ·v0=vT,即是在观测站O1处相对于目标来波方向的切向运动速度值。

由此可见式(10)与式(4)是完全一致的,即在双站测向交叉定位中将2个站看成是由一个运动站在不同时刻对同一目标的测向后实施交叉定位,且当2个观测时刻间隔ΔT非常小时,双站测向交叉定位的理论计算公式与基于切向运动测距的单站定位理论计算公式是一致的。
上述短的观测时间间隔代表短的运动距离,同时也意味着短的定位基线。这也说明:可以将基于切向运动测距的单站定位看成是短基线条件下的多站测向交叉定位。
3.2 两种定位方法在数据处理上的统一性分析
基于切向运动测距的单站定位理论计算式似乎比较完美,从理论上讲可以通过式(4)实现瞬时定位。但是在实际应用中,由于角度变化率的测量问题,通常需要一个观测时间段才能完成整个定位过程。相关综述文献报道的基于相位差变化率的单站定位精度达到2%R(R为距离)量级,定位速度一般在20s量级[1]。在20s的时间内,单个观测站运动的距离大约在几km量级,而观测站与目标之间的距离也在百公里量级。这一过程中该观测站是连续不断地在实施对目标的测向,也就是说,该观测站可以获得一个来波方向角的时间序列值θ(t),然后通过θ(t)对时间t的微分运算来得到角度变化率的估计值,如图2所示。
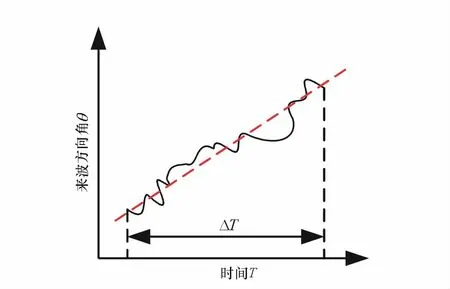
图2 单站定位中连续测量来波方向角的时间序列示意图
在观测时段ΔT很小的条件下,从理论上说,来波方向角θ与时间T之间应该近似成线性关系,如图2中的虚直线所示。该直线对应的斜率就等于角度变化率˙θ。但是由于噪声与测量误差的影响,实测曲线如图2中实曲线所示。为了获得角度变化率,就需要采用最小二乘法进行直线拟合,然后通过拟合出的直线对应的斜率来作为角度变化率的实测值。在工程应用中,可使用干涉仪通过通道间相位差测量来获得来波方向角的时间序列,而所谓的干涉仪的相位差变化率就对应了来波方向角的角度变化率。
目前已有一些文献报道了各种角度变化率测量方法[4-8]。文献[4]对干涉仪2个接收通道接收到信号与本振信号进行正交混频,对正交混频后的复信号进行离散傅立叶变换(DFT),然后进行复数相乘,经过低通滤波后估计出相位差变化率。文献[5]提出将干涉仪两通道接收到的信号进行相乘滤波,然后保留低频分量进行模/数(A/D)变换,经过一个测频单元即可输出相位差变化率的测量值,并在此基础上通过正交移相方法将待测过程转换为复过程,从而解决了过窄的源信号脉冲宽度和过低的相位差变化率等问题。虽然类似的方法还有许多,但是上述方法从数据处理上说,都可以统一为对时变的角度测量值θ(t)的微分运算,来得到的角度变化率的估计值˙θ^的估计值,只不过采用了不同的实现途径而已。
这说明基于切向运动测距的单站定位的基本数据来源于一段观测时间ΔT内的θ(t)值,而多站测向交叉定位理论所采用的基本数据同样来源于θ(t),只不过单站定位将θ(t)看成是一个时间的函数,而多站定位将θ(t)看成是一个空间位置的函数,只是思考问题的角度不同,实际上2种定位理论所采用的原始测量数据是一致的。所以多站测向交叉定位对上述数据处理后所获得的定位精度,与单站定位对上述数据处理后所获得的定位精度应该是大致相同的,这说明2种定位方法在相同的边界应用条件下,具有相同的几何精度因子(GDOP)。这也从另一个方面说明了二者在理论模型上具有一定的统一性,详细分析如下:
(1)用于多站测向交叉定位求解的最小二乘算法
设共有N+1个观测站,第i个观测站坐标为di,目标坐标为(xT,yT),i=0,1,2,…,N,二者之间的距离记为ri,该观测站相对于目标的真实方位角为θi,实际测量得到的方位角为θi,M,其所对应的方位角的测角误差为,将上述N+1个观测站看成由一个观测站沿X轴正向直线运动形成,于是有如图3所示。
如前所述,在观测时段ΔT很小的条件下,真实方位角度序列值θi与时间T之间近似成线性关系,

图3 多站测向交叉定位算法示意图

式中:

另外值得注意的是:在处理序列化测向的多站测向交叉定位时,没有采用传统的布朗最小二乘三角定位算法[3],而是将多次测向交叉定位过程通过最小二乘法拟合,转化成了双站测向交叉定位过程,而转化之后的2个观测站具有这一过程中的最长的定位基线。(2)用于单站定位中角度变化率求解的最小二乘算法如前所述,运动单站对固定目标定位时,工程实现本质上也是在角度测量后通过最小二乘拟合来得到角度变化率参数。如果将单观测站每一次角度测量看成是多个观测站的序列化行为,则第i次角度测量值为θi,M,对应的角度测量偏差 Δθi,M=θi,M-θi,则图2中拟合出的直线要使得对应的各次测量的
于是由最小二乘法可得:

由此求得A = [θ0,θN]T之后,结合S =v0·ΔT,利用式(5)即可计算出辐射源与(x0,y0)之间的距离r为:角度偏差的平方和最小,即使得最小化。这一过程与前面的式(12)是完全相同的,最小二乘得到的结果如式(13)所示,相应的角度变化率参数˙θ为:

根据基于切向运动测距的单站定位计算公式(4),可以得到辐射源与(x0,y0)之间的距离r为:

通过上述2种数据处理方法得到的结果对比可知,在观测时段ΔT很小的条件下,有θN≈θ0成立,即按照式(14)计算得到的多站测向交叉定位的结果,与按照式(16)计算得到的基于切向运动测距的单站定位的结果基本一致。这说明二者在数据处理上具有统一性。
在上面的多站测向交叉定位中的最小二乘是一种批处理,因为各个观测站几乎可以同时获得方位角的测量值,而基于切向运动测距的单站定位中所获得的方位角测量值不是同时得到的,而是该观测站运动到不同的位置后按序得到的。实际上这并不是问题的本质,如果将运动单站在不同位置的测量看成是一种特殊的多站,而多站测量值也是按序得到的,那么两者都可以统一进行处理,这样就可以用递推最小二乘来统一解释2种定位过程,而递推最小二乘也反映了一个定位结果逐步收敛的过程,这与目前工程实际中基于切向运动的单站定位输出结果的收敛过程曲线是吻合的。
由于批处理的最小二乘法与递推最小二乘法在各类文献中都有相关报道,属于相对比较成熟的信号处理理论,在此就不再展开阐述了,在后续仿真过程中再直接应用相关计算公式进行分析。
4 仿真验证
仿真场景如下:在(20 000,80 000)m处有一部相控阵雷达对空搜索,1架飞机以250m/s的速度从原点沿X轴正向运动,该雷达每间隔0.1s会对飞机进行1次照射,每次照射只辐射1个脉冲,飞机上搭载有用于无源测向定位的干涉仪,只能截获雷达主瓣信号,所以在此场景下干涉仪每0.1s会输出一个对该雷达辐射脉冲的测向数据。飞机在20s的时间内对该雷达实施无源定位,干涉仪在这一过程中一共输出201个测向数据,整个仿真场景如图4所示。

图4 仿真场景示意图
图4(a)和(b)分别表示测量起始时刻和终止时刻飞机与雷达之间的相对位置。在这一过程中,干涉仪对雷达脉冲进行测向得到的201个测量值的角度值序列如图5所示。
(1)采用批处理的多站测向交叉定位
将上述201个测向数据看成为201个观测站获得测向结果,201个观测站的坐标分别为:(25k,0),k=0,1,2,…,200,按照批处理最小二乘算法获得θ0和θ200,利用式(14)可求得雷达坐标为:(19 689,78 216)。
(2)采用基于切向运动测距的单站定位
干涉仪输出的直接数据是通道间的相位差,这对应着测向角度,由测向角度时间序列可以求得角度变化率。通过角度变化率来估计距离,然后结合当前的测向值来计算辐射源的位置,这是一个逐渐收敛的过程,整个过程中估计的定位误差的变化曲线如图6所示。
在经过201次迭代后,可求解得到雷达的坐标为:(19 643,78 030)。
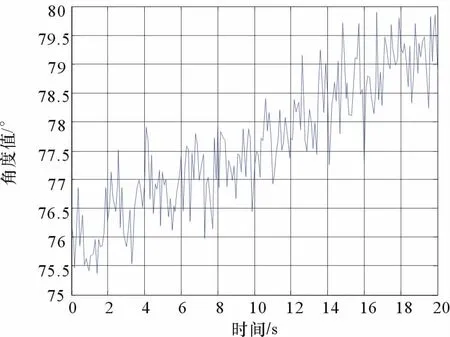
图5 干涉仪获得201个测向数据图

图6 单站定位的定位误差变化曲线
(3)采用递推最小二乘处理的多站测向交叉定位
如前所述,将201个测向数据看成是同一个运动观察站在201个位置上对同一固定目标的测向结果,该观测站按照时间顺序可以依次输出200个定位结果,第m次的输出相对于前m-1次来说新增加了1次测向数据,这样第m次的定位计算相对于前m-1次来说,信息量更大,定位结果也更趋于准确,采用递推最小二乘来处理这一多站测向问题,在这一过程中,定位误差的变化曲线如图7所示。
在经过200次迭代后,求得的雷达坐标为:(19 689,78 216)。由上述仿真结果的对比可见,整个定位过程2种方法输出的定位结果和定位收敛过程几乎完全一致。这说明了该单站定位体制与多站定位体制在理论模型上的统一性。
5 结束语

图7 递推最小二乘的多站测向交叉定位误差变化曲线
本文在对基于切向运动测距的单站定位理论模型与多站测向交叉定位理论模型简要概述的基础上,分别从时间尺度与数据处理2个方面揭示了单站定位与多站定位之间的紧密联系,并通过仿真对分析结果进行了验证,说明了多站测向交叉定位与基于切向运动的单站定位具有统一的理论模型。这一理论分析结果也为无源定位系统的多功能应用奠定了基础。
[1]黄登才,丁敏.测相位差变化率无源定位技术评述[J].现代雷达,2007,29(8):32-37.
[2]孙仲康,郭福成,冯道旺,等.单站无源定位跟踪技术[M].北京:国防工业出版社,2008.
[3]Poisel Richard A.Electronic Warfare Target Location Methods[M].USA Boston:Artech House,2005.
[4]万方,丁建江,郁春来.一种雷达脉冲信号相位差变化率测量的新方法[J].系统工程与电子技术,2011,33(6):1257-1261.
[5]邓新蒲,祁颖松,卢启中,等.相位差变化率的测量方法及其测量精度分析[J].系统工程与电子技术,2001,23(1):20-23.
[6]郭福成,贾兴江,黄甫堪.仅用相位差变化率的机载单站无源定位方法及其误差分析[J].航空学报,2009,30(6):1090-1095.
[7]陈大昊,游志刚,张剑云,等.基于相位差变化率方法的双基线相位解模糊[J].现代雷达,2006,28(6):19-22.
[8]单月晖,孙仲康,皇甫堪.基于相位差变化率方法的单站无源定位技术[J].国防科技大学学报,2001,23(6):74-77.
