跟踪临近空间目标的衰减记忆最小二乘算法

吴 超，单 奇，邵俊伟

（中国电子科技集团公司38所，合肥230088）

0 引 言

临近空间又称为亚轨道或空天过渡区，包括大气平流层区域、中间大气层区域和部分电离层区域。根据国际航空联合会的定义，临近空间的范围确定在23～100km[1]。

随着临近空间的战略价值引起美国为首的航天大国的关注，近年来各军事强国竞相着手研发各类低速和高速临近空间武器。其中，对我国国土防空威胁最大的当属临近空间高超声速武器。临近空间高超声速目标包括高超声速巡航导弹（速度3.5～7Ma）、高超声速飞机（速度4～10Ma）、高超声速空天飞行器（速度8～20Ma）等。临近空间高超声速目标能够在稀薄大气层作持续的高超声速飞行，具有飞行速度快、机动性高、投送能力强、突防能力好等特点，能够实施高空侦察、临空轰炸、远程快速精确打击时敏目标，甚至执行1h之内全球打击，即“全球常规快速打击（CPGS）”。

2010年美国相继开展了 X－37B、HTV－2和X－51A等临近空间高超声速飞行器试验，这些试飞事件标志着美国空军将以无人驾驶可重复使用的高超声速飞行器，把在蓝色天空开展的情报收集、目标攻击与通信等任务向黑色太空的空天领域推进，美国正基于这种手段谋求核武器和高超声速飞行器双重战略威慑能力。根据美军发展计划，临近空间高超声速巡航导弹、助推滑翔（巡航）类导弹和临近空间高速无人机等将在2015年前后装备部队，临近空间轨道再入飞行器也将在2020年左右具备作战能力。

临近空间高超声速飞行器的出现，模糊了传统的战略导弹与战术导弹的区别，削弱了传统的战略纵深在国土防御中的作用。为应对即将出现的威胁，加强对临近空间的探测已经成为必然趋势。对于雷达系统而言，研发针对临近空间高超声速武器的跟踪技术势在必行。

目前，国内对于临近空间目标的跟踪技术研究尚处于起步阶段，关欣等[2]对临近空间目标跟踪做了概述，提出一些改进跟踪算法的思路，但没有给出工程应用的跟踪算法；李昌玺等[3]提出了一种自适应不敏卡尔曼滤波算法，给出了一类简单轨迹的跟踪分析，但是缺乏对不同飞行轨迹跟踪算法性能的探究。由于临近空间高超声速飞行器具备重要的战略价值，国际上公开介绍这类目标的跟踪方法更是稀缺。针对临近空间高超声速目标跟踪的问题，本文提出了一种衰减记忆的最小二乘跟踪方法。新方法不需要对目标运动方程或是机动加速度提出任何先验假设，不存在运动方程失配导致滤波发散的风险，比依赖运动方程的跟踪方法具有更强的鲁棒性。

1 临近空间高超声速目标跟踪方法

1.1 传统滤波方法面临的困难

国内外雷达数据处理多采用α－β滤波、卡尔曼滤波、自适应卡尔曼滤波或者交互多模型等方法，在滤波过程中使用匀速（CV），匀加速（CA），Singer，匀速转弯（CT）等运动模型[4]。这类数据处理技术往往只能实现3Ma以下速度的目标跟踪。同时卡尔曼滤波及其衍生滤波方法的精度严重依赖目标运动模型的选择，当目标运动模式与滤波模型匹配时，算法精度高；当目标运动模式与滤波模型不匹配时，算法精度大幅下降，甚至导致滤波器发散、目标失跟。

而在临近空间目标的跟踪中，雷达需要面对的是具有20Ma以上的速度，具有高机动能力、种类繁多的对象。总体上，临近空间高速目标可分为超高速巡航导弹、超高速无人飞机、轨道式再入飞行器3类。其飞行轨迹可以归纳为图1所示的2类典型飞行特征[1]。

由于国外的技术封锁，目前我国对临近空间高速目标飞行轨迹的认识仅止于仿真实验的阶段，没有精确的数学模型可用于研究。所以，依赖跟踪模型的卡尔曼类算法在工程应用中鲁棒性不强，具有滤波发散的风险。

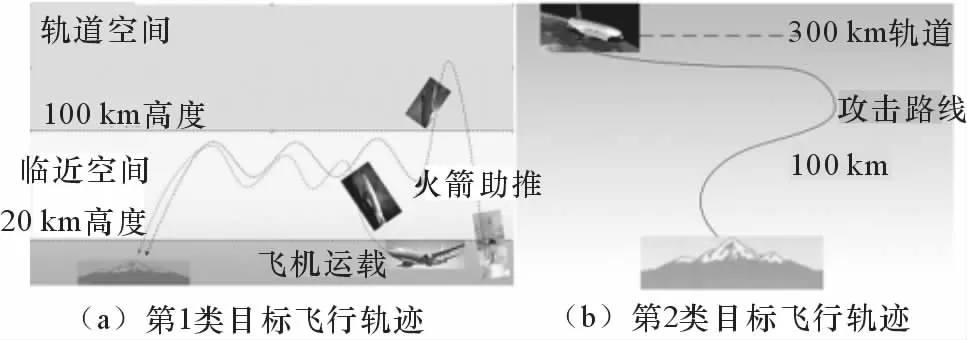
图1 临近空间目标2类典型飞行轨迹示意[1]

1.2 最小二乘滤波算法

最小二乘滤波算法是一种批处理算法，适合于处理运动模型不能精确确定的目标跟踪问题。

根据文献[5]，设对某一运动过程y（t）进行了n次测量，得到1组测量值｛～yi｝，i＝1，2，…，n。～yi用来表示在ti时刻得到的y（ti）的量测值。由于在量测中存在随机误差，假定～yi＝y（ti）＋ei，其中ei是不相关的随机误差，其期望值为0，方差为σ2。令：

式中：E（e）为e的期望值；E（eeT）为e的斜方差。

最小二乘方估计可以写成：

根据计算，最小二乘方估计＾a为：

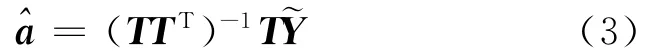
其协方差矩阵为：

1.3 衰减记忆的最小二乘滤波方法

最小二乘滤波方法对于目标的运动模型和机动输入的统计特性不需要先验的假定，适合对运动方式难以精确刻画的目标做跟踪。常规的最小二乘滤波在对当前时刻的目标状态进行滤波时计算了所有的历史量测点，但是由于临近空间超高声速目标速度快，机动能力强，最小二乘滤波这种全局批处理的模式会延迟算法对目标机动的响应，导致机动段跟踪误差的扩大。显然，原始的最小二乘滤波不适合直接应用到机动性强的临近空间目标跟踪。基于上述情况，改进了最小二乘滤波算法，只对距离当前时刻一定时间间隔内的量测点进行批处理，而更早的历史点迹不计入批处理计算，形成衰减记忆最小二乘滤波方法。该方法既保留了最小二乘滤波鲁棒性强的优点，又通过使用局部历史点对当前量测进行滤波，避免了使用全局数据导致的机动响应延迟。

衰减记忆最小二乘跟踪方法如下：

每次获得新的量测点迹M（i），

（1）使用三维修正无偏量测转换，将雷达极坐标系的量测点迹转换到雷达直角坐标系；

（2）根据衰减记忆历史，选取局部历史量测点迹 M（i－k＋1），…，M（i）作为输入的量测数据，使用最小二乘方估计方法计算当前滤波点的X，Y，Z位置；

（3）将（2）计算出的X，Y，Z坐标反算回雷达极坐标系。

在使用衰减记忆最小二乘时，X，Y，Z坐标相对时间的多项式是一阶的，记忆长度离线设定。

2 仿真实验

实验采用Matlab（2008a）软件进行仿真计算。根据文献描述[6-7]的方程，仿真生成了临近空间高超声速飞行器在6Ma速度和20Ma速度的飞行轨迹，并在2Hz数据率下分别进行了跟踪实验。仿真雷达探测距离精度50m，方位精度0.2°，仰角精度0.15°生成量测数据。实验采用蒙特卡罗仿真（独立运行100次）分析跟踪滤波结果。

2.1 实验场景一

最高速度6～8Ma速度的目标仿真。取关机点参数为以下值：

速度：Vk＝2.0km／s；

航迹倾角：γk＝45°；

航迹方位角：χk＝90°；

高度：hk＝50km；

经度：λk＝120.321 1°；

纬度：φck＝33.804 5°；

雷达最远观测距离：1 200km。

飞行器以6～8Ma速度飞行，运动轨迹和滤波航迹如图2所示。在雷达观测范围内，飞行器以近似正弦波轨迹飞行，经历了2个波峰和1个波谷。从图上看，滤波航迹围绕在真实航迹的周围，滤波效果较好。

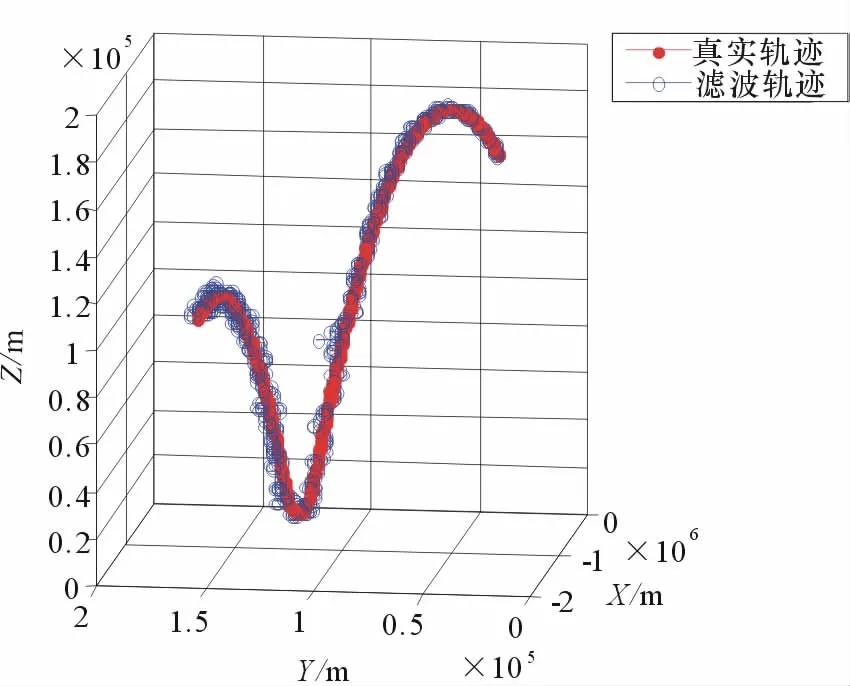
图2 实验场景1的滤波航迹与真实轨迹

图3的3个子图分别是滤波航迹在X，Y，Z 3个维度上的距离均方根误差值，其中圈号线是滤波位置均方根误差曲线，加号线是量测的位置均方根误差曲线。可以看到衰减记忆的最小二乘滤波在跟踪到第20步开始收敛，在整个跟踪过程中滤波误差明显小于量测点迹在各个维度的误差。

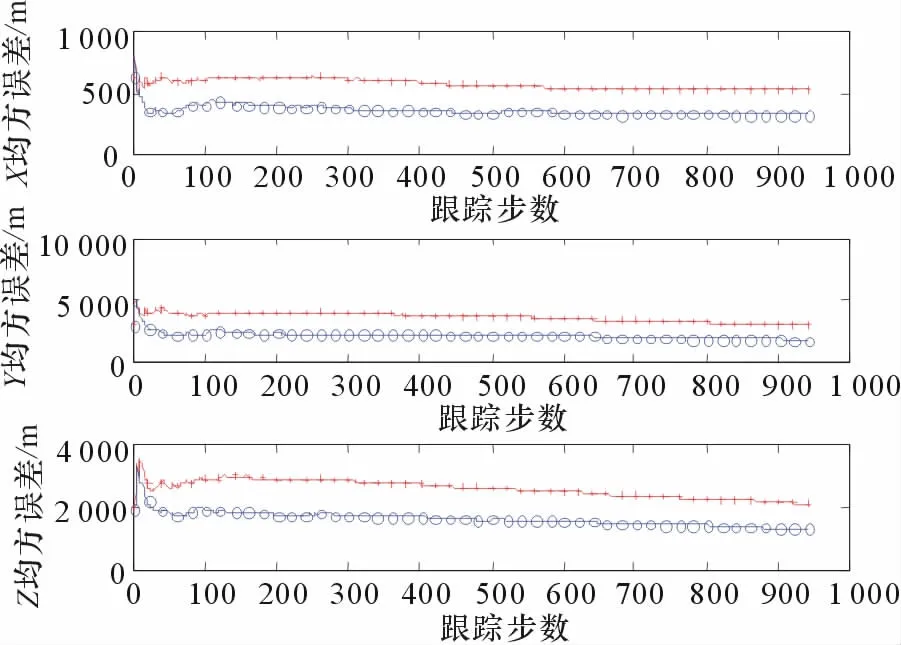
图3 实验场景1滤波航迹的位置均方误差

2.2 实验场景2

最高速度20Ma以上的目标仿真。取关机点参数为以下值：

速度：Vk＝6.8km／s；

航迹倾角：γk＝45°；

航迹方位角：χk＝90°；

高度：hk＝100km；

经度：λk＝120.321 1°；

纬度：φck＝33.804 5°；

雷达最远观测距离：1 200km。

20Ma目标的运动轨迹和滤波航迹见图4，飞行器向下飞行经历波谷后向上飞行。与场景1相比，场景2的拐弯段的轨迹更加陡峭。可以看到，对20Ma目标，滤波算法保持了稳定跟踪。

图4 仿真场景2的滤波航迹与真实轨迹

图5是滤波航迹在X，Y，Z3个维度上的距离均方根误差值。滤波算法在第20步附近收敛，在整个跟踪过程中滤波误差小于量测点迹在各个维度的误差，跟踪滤波的收益比场景1略小。

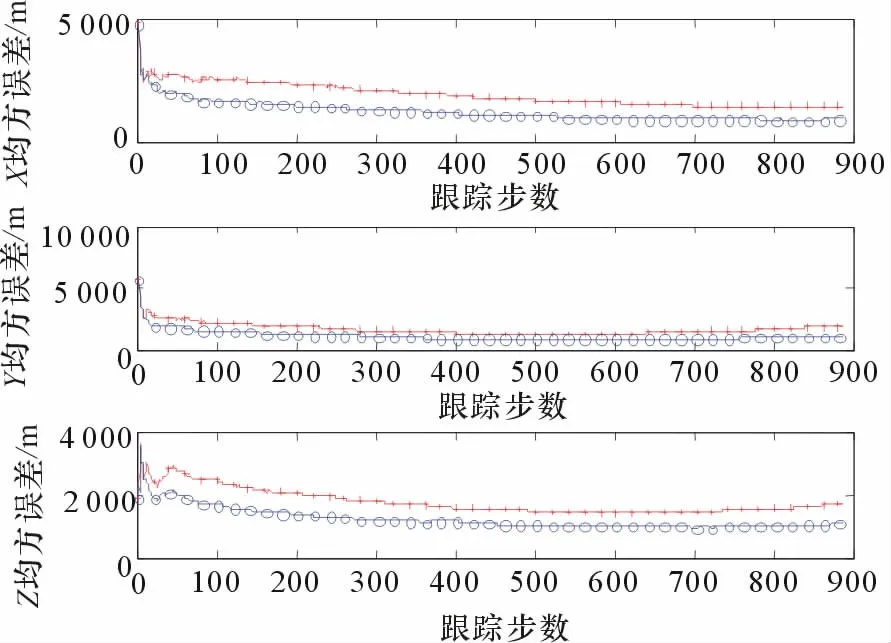
图5 仿真场景2滤波航迹的位置均方误差

表1记录了衰减记忆的最小二乘滤波算法反算回雷达极坐标系的全局距离均方根误差和全局方位均方根误差。在跟踪6Ma目标时，滤波算法距离误差比量测减小32.8%，方位误差减小38.1%，仰角误差减小40.0%；跟踪20Ma目标时，滤波算法距离误差减小35.9%，方位误差减小40.0%，仰角误差减小33.3%。

从实验结果来看，无论6～8Ma还是20Ma的高超声速临近空间目标，本文提出的衰减记忆最小二乘滤波算法都可以实现稳定跟踪。对于目标飞行的机动段，衰减记忆最小二乘滤波跟踪连续光滑。相比于量测数据，新算法在距离、方位、仰角都获得了超过30%的精度提高。

表1 衰减记忆最小二乘算法的均方根误差对比

3 结束语

临近空间高超声速目标数据处理与常规雷达数据处理最大的不同是跟踪高速高机动目标，高超声速飞行器的运动速度可能达到20Ma以上。空间目标的运动一般是有规律的，而临近空间高超声速飞行器在机动能力和突防能力上有突出的特点。因此，受限于特定运动模型的卡尔曼类滤波算法在跟踪临近空间高超声速目标时，有运动模型不匹配滤波发散的风险，鲁棒性不强。

针对上述问题，本文提出了一种衰减记忆的最小二乘滤波算法。该算法以最小二乘为基础，考虑到目标高机动特性，每获得一个量测，就以时间维度的局部量测值作为算法的输入进行迭代滤波。仿真实验表明，新算法能稳定跟踪6Ma与20Ma目标，目标机动段跟踪连续光滑，距离、方位、仰角的跟踪精度较高。同时新算法不需要预设运动方程，鲁棒性强。

[1]张国华.临近空间目标探测分析[J].现代雷达，2011，33（6）：13－19.

[2]关欣，赵静，何友.临近空间高超声速飞行器跟踪技术[J].四川兵工学报，2011，32（8）：4－6.

[3]李昌玺，毕红葵，王红，等.一种临近空间高超声速目标跟踪算法[J].航天电子对抗，2012，28（4）：10－13.

[4]何友，修建娟，张晶炜，等.雷达数据处理及应用[M].北京：电子工业出版社，2009.

[5]徐振来.相控阵雷达数据处理[M].北京：国防工业出版社，2009.

[6]肖业伦.航空航天器运动的建模——飞行动力学的理论基础[M].北京：北京航空航天大学出版社，2003.

[7]孙勇，段广仁，张卯瑞，等.高超声速飞行器再入过程改进气动系数模型[J].系统工程与电子技术，2011，33（1）：134－137.