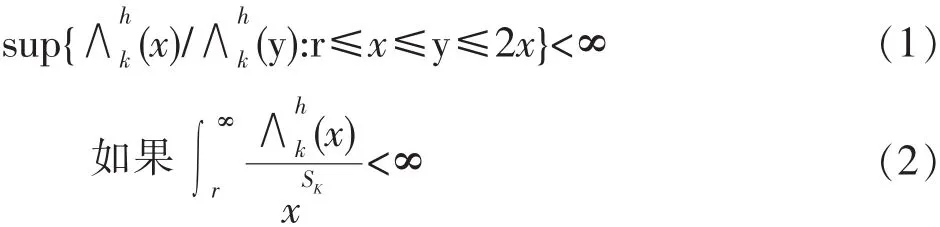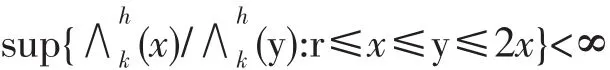通弦路径与上半平面圆及矩形的相交概率
2013-08-09梁静
梁静
(淮南师范学院 数学与计算科学系,安徽 淮南 232038)
数理化研究
通弦路径与上半平面圆及矩形的相交概率
梁静
(淮南师范学院 数学与计算科学系,安徽 淮南 232038)
在上半平面H中一条通弦SLEk路径与一个圆心在实轴上的半圆相交概率的基础上,给出了上半平面中H中一个圆与通弦SLEk路径相交的概率估计;同时得出上半平面H中一条通弦SLEk路径与一个矩形相交的概率估计。
SLE;相交概率;吞并时间;限制性质
引言
随机洛纳演变(SLE)是由O.Schramm①O.Schramm.Scaling limits of loop-erased random walks and uniform spanning trees,Isral J.Math, 2000,118:221-288.在研究一些统计物理的二维模型中,成功运用并得到严格数学结果的一族一元随机增长过程。②Steffen Rohde and Oded Schramm.Basic properties of SLE,Ann.of Math,2005,161(2):883-924.中研究了SLE的基本拓扑和几何性质③V.Beffara.Hausdorff dimensions for SLEk,Ann.Prob,2004,32:2606-2629.,中确定了SLE6曲线外界的Hausdorff维数,若干年后④V.Beffara.The dimensions of the SLE curves,Ann.Prob,2008,4:1421-1452.,证明了SLE曲线的Hausdorff维数是更多内容请参阅⑤J.Cardy.SLE for theoretical physicists,Ann.Physics,2005,318:81-118.⑥G.F.Law ler.Conformally Invariant Processes in the Plane,American Mathematical Society.RI,2005.G.⑦W.Werner.Random p lanar curves and Schramm-Loewner evolutions,Lectures on probability theory and statistice.,Lecture Notes in Math,1840,pp.107-195,Springer,Berlin,arXiv:math.PR/0303354.⑧I.A.Gruzberg and L.P.Kadanoff.The Loewner equation:maps and shapes,J.Statist.Phys,2004,114:1183-1198.。当0≤k≤4,曲线是简单的,仅在原点与R相交。当k≥8,曲线是充满上半平面H的,因而r[0,∞)∩R=R。[9]中讨论了上半平面H中一条通弦SLEk路径与圆心在实轴上的一个半圆的相交概率,在本文中推导出了上半平面H通弦SLEk路径与圆周相交的概率,证明了如果0
1 预备知识
在这一节给出本文涉及到的一些定义、记号以及一些基本事实,更详细的请参见文[9][10][14]等。
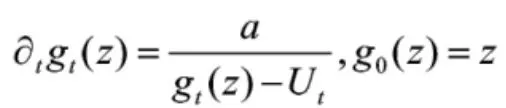
其中z∈H,Ut=-Bt是B0=0的标准一维布朗运动。对z∈H,令Tz表示通弦洛纳方程的第一次爆破时刻,壳Kt={z∈H:Tz≤t}。{K1,t≥0}是H中递增紧集族,gt是从HKt到H上的一个共形变换。对所有的k>0,存在一条连续曲线γ:[0,∞)→H且γ(0)=0,使得HKt是Hγ[0,t]的无界连通分支。曲线γ的行为仅与k有关,如果那么 γ是条简单曲线且如果(i.e.,4 如果ε>0,z∈C,记B(z;ε)={ω∈C:|z-ω|<ε}表示以z为球心,ε为半径的球。如果x∈R,那么D((x, rx;ε))=B((x,rx;ε)∩H)={x+irx+ρeiθ:0<θ<2π,0<ρ<ρε},C((x,rx;ε))=B((x,rx;ε)∩H)={x+irx+εeiθ:0<θ<2π}分别表示上半平面上以(x,rx)为中心,ε为半径的圆盘和圆周。表示存在非零,有限常数c1,c2使得此外,g(r)~h(r)表示当 r→0。 文[9]已讨论了通弦SLEk路径与半圆周相交的概率,在这一节,我们用类似的方法给出了一条通弦SLEk路径与上半平面中圆周相交的概率,不同之处在于我们分别考虑上下两个半圆周与通弦SLEk路径相交的概率。 定理1:假设x>0是一个实数,0 我们要证明定理1,首先需要以下结果: 命题1:令a(z0)∈(0,π)表示z0的辐角,ε>0,那么,当k∈(0,8),我们有以下估计 当k≥8,对所有的ε>0,此概率等于1。 证明:这个命题的证明见[4]。 命题2:设γ表示当k≤4时的一条通弦SLEk路径,z=reiθ为H中的一点。如果令f(z)=P{z在γ[0,∞)右侧},那么由仅依赖于θ的尺度性,f(θ)=特别地,当时,P{z在 γ[0,∞)右侧 证明:这个命题的证明见[11][12]。 在命题2的基础上可得到下列引理: 引理1:令z=ρeiθ∈H,f(z)=P{z在γ[0,∞)左侧}, 图1 圆被以{z±n,n=0,1,…}为圆心的圆盘所覆盖 图2 点z=x+i3rx在γ[0,∞)左边2 定理3:令0 证明:由图2可清楚看出P{γ[0,∞)∩ C((x,rx);左边},因为 arg(x+i并且因为2sin t≥t对由引理1可得 对0≤t≤1,8arctant≥πt,上式就暗示了存在一个常数ca,即 对0≤t≤1,8arctant≥πt,上式就暗示了存在一个常数ca,即使得P{γ 图3 点左边 图4 γ[0,∞)与线段AB相交 定理4:令0 证明:很显然,如果 γ[0,∞)与线段 AB相交,那么它一定与圆周相交,如图 4,由 推论1:令x>0是个固定实数,并且假设0< ε≤x,如果γ:[0,∞)→H是从0到∞的通弦SLEk路径,且那么 P{γ[0,∞)∩ C((x,ε);其中是上半平面中以(x,ε)为圆心为半径的圆周。 由[6]中定理6.1可得下述命题: 命题3:如果γ:[0,∞)→H是从0到∞的通弦SLEk路径,且A是H的一个有界子集,使得HA是单连通的,A=H∩A,0A,那么P{γ[0,∞)∩ A=其中ΦA:HA→H是HA到H上的唯一共形变换,且ΦA(0)=0,ΦA(z)~z,当z→∞。 在这一节,我们将给出上半平面中一条通弦SLEk(k≤4)路径与一个矩形相交的概率估计。 引理2:令k∈(0,4],且γ是通弦SLEk路径,固定r>1,假设h:[r,∞)→(0,∞)是连续且满足下列条件 证明:这个引理的证明见[10]。 在此引理的基础上可得下列定理: 定理5:令k∈(0,4],且γ是一条通弦SLEk路径,固定r>1,h:[r,∞)→(0,∞)是连续且满足下列条件: 证明:令ρ:[r,∞)→(0,∞)是一个函数使得 令x>0且tx:=sup{t≥0:x埸Kt},那么我们知道tx=∞,如果k≤4;tx<∞,如果k>4。对t∈(0,tx),定义M由(4)可知Z0<∞。因为对每个x>0都是上鞅,从而Zt是一个上鞅。因为(2)中的积分是有限的,可知存在一个有限的使得固定 R>R0,令 A:={x+iy:x≥R,y≤h(x)},令 TA:=inf {t≥0:γt∈A},且在事件TA<∞上令x0:=Reγ(TA),y0= Imγ(TA)。从我们对R的选择,有由[10]中的引理2.2,对每个x>x0+y0。因而在事件因为Zt是上鞅,由随机抽样定理可得Z0≥E 定义X:={x≥r:x∈塬h(x)},令X)dx,那么由(6)式和[10]的命题2.3,有E(Qa)=1,即从而 由定理2,我们得到: 推论2:令k∈(0,4],且γ是一条通弦SLEk路径,固定记A={x+iy:r≤x≤2r,0≤ εy≤ε}。那么当k>4时;当k=4时 Intersection probabilities for a chordal SLE path and circle and a rectangle in the upper half plane L IAGN Jing On the basis of the probability that a chordal SLEkpath in the upper half plane Hintersects a sem icircle on the real line,we derived the probability that a chordal SLEkpath in the upper half plane intersects a circle in the upper half plane H.And we concluded the probability that a chordal SLEkpath in the upper half plane intersects a rectangle in the upper half p lane H. SLE;intersection probability;swallowing time;restriction property O177.1,O152.21 A 1009-9530(2013)04-0094-05 2012-09-28 淮南师范学院科学研究项目(2011LK78) 梁静(1981-),女,淮南师范学院助教,硕士,主要研究方向:随机洛纳发展。2通弦路径与上半平面圆周的相交概率


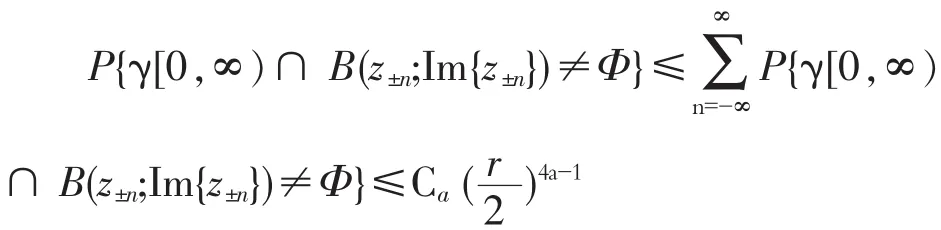


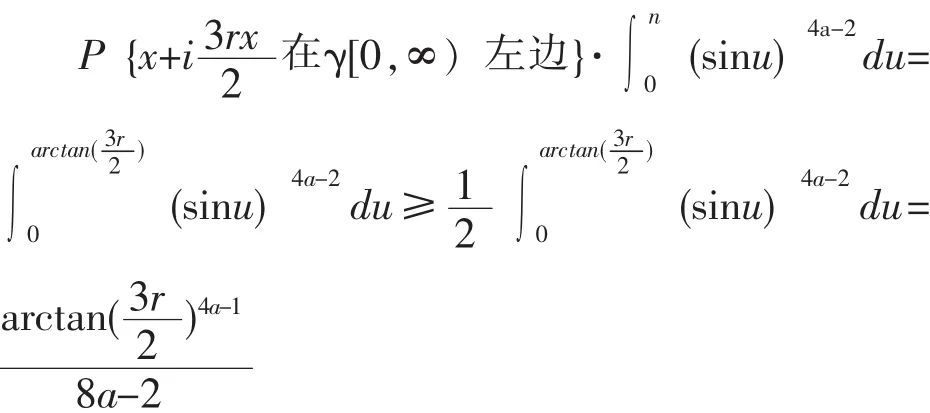
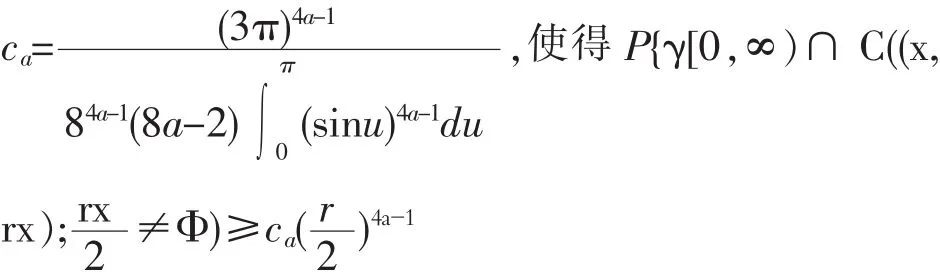


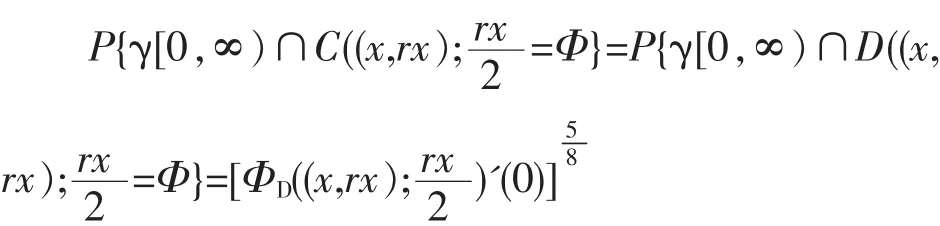
3通弦路径与矩形的相交概率