消力坎式消力池淹没系数和坎高的计算

张志昌，李若冰，赵 莹，傅铭焕

（西安理工大学水利水电学院，西安 710048）

消力坎式消力池淹没系数和坎高的计算

张志昌，李若冰，赵 莹，傅铭焕

（西安理工大学水利水电学院，西安 710048）

为了研究消力坎式消力池淹没系数和消力坎高度的简化计算方法，以取代传统的试算法。综合前人对消力坎淹没系数的研究成果，对淹没系数进行优化拟合，进而推求淹没系数的迭代公式；分析了消力池坎高的简化计算方法；通过动量方程研究消力坎的阻力系数。研究给出了淹没系数的拟合公式和迭代公式、坎高的简化公式以及消力坎阻力系数的计算公式，并通过实例验证了公式的正确性。结果表明，淹没系数的迭代公式和坎高的简化公式形式简单，避免了试算的困难。

消力坎式消力池；淹没系数；坎高；阻力系数；迭代计算

1 问题的提出

底流消能是水工建筑物的三大消能方式之一，历史悠久，应用广泛，适合于大、中、小型水利工程［1］。苏联的萨杨舒申斯克坝、印度的巴克拉坝、巴西的河床式水电站，我国的安康水电站、五强溪水电站、长江葛洲坝河床式水电站、二江泄洪闸、三江冲沙闸、荆江分洪闸等均采用底流消能［2］。

底流消能的形式之一是消力坎式消力池［3］，适应于河床不宜开挖或开挖太大造价不经济的情况。消力坎的作用是壅高坎前的水位形成消力池，其水力计算的主要任务是确定坎高e和池长Lk［4］。本文主要研究坎高的确定方法。

目前对消力坎式消力池坎高的计算主要为传统的试算法，其过程繁琐。为了简化计算，文献［5］介绍了一种简化计算方法，也称为巴什基洛娃表解法，此方法根据传统计算方法的原理，事先计算成表格，在计算时查用。文献［6］根据巴什基洛娃对消力坎淹没系数的研究成果，给出了淹没系数的三次方程，经分析该方程误差较大。文献［7］根据坎控水跃的原理，计算了坎高和水跃长度，认为坎高比传统计算方法略高了7%。文献［8］根据级数展开方法，把求解跃前水深的三次方程变成了显式计算，使跃前水深的计算得到了简化。文献［9］在消力坎的淹没出流计算中，按照传统试算法的过程计算淹没系数。文献［10－11］给出了消力坎式消力池高度计算的程序，把消力坎的淹没系数编写在程序中以便调用。文献［12］对消力坎计算的每个公式采用分步迭代计算，以求得消力坎的高度，为了迭代方便，对巴什基洛娃的淹没系数给出了一个拟合公式，在迭代时给定坎高一个初值，即可计算出坎高。文献［13］用动量方程推求了消力坎的阻力，认为阻力是下游水深的函数，但未给出阻力系数的计算方法。文献［14］通过试验研究了闸下出流消力坎淹没水跃的水力特性，得出了不同消力坎高度、宽度和淹没度下消力坎的阻力系数，给出了闸前水深与跃后共轭水深和下游水深的关系。文献［15］根据因次分析法，通过试验研究了不同消力坎高度下共轭水深与弗劳德数的关系；研究表明，弗劳德数越大所要求的消力坎高度越大，共轭水深随着消力坎高度和弗劳德数增大而增大，但试验点据比较分散。文献［16］研究了空间水跃下消力坎的共轭水深、水跃相对长度和相对扩散宽度对消能率的影响；研究表明，共轭水深、水跃相对长度随着相对扩散宽度的增大而减小，消能率随着相对扩散宽度的增大而增大，并给出了不同坎高、不同消力坎位置情况下共轭水深的关系，对研究空间水跃具有重要的参考价值。

由以上论述可以看出，消力坎式消力池坎高的计算公式中含有淹没系数，而淹没系数又与坎高有关，目前尚无显式计算方法。本文分析了前人的研究成果，给出了淹没系数和坎高的迭代计算方法，该方法不需要试算，可以直接计算消力池的深度和坎高，给工程设计提供了方便。

2 消力坎式消力池坎高传统计算

2．1 传统计算方法

消力坎式消力池如图1所示。建坎后水流受坎壅阻，坎前水深hT大于下游水深ht，池内形成水跃。从图1可以看出hT＝e＋H1。式中：hT＝σjh″c，其中σj为水跃的淹没系数，h″c为跃后水深；e为坎高；H1为坎上水深。

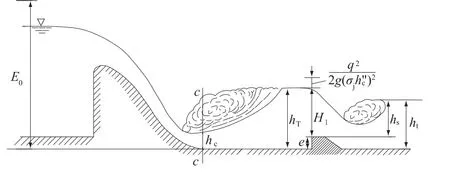
图1 传统消力坎式消力池Fig．1 Traditional stilling basin of sill-type

由此可得坎高e的计算公式为

消力坎一般做成折线形或曲线形实用堰，故坎顶水头可用堰流公式计算，即

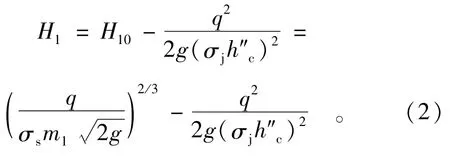
式中：H10为消力坎上的总水头；q为单宽流量；g为重力加速度；m1为消力坎的流量系数，与坎的形状及池内水流状态有关，目前尚无系统的研究资料，初步设计时可取m1＝0．4～0．42；σs为消力坎的淹没系数；跃后水深h″c为

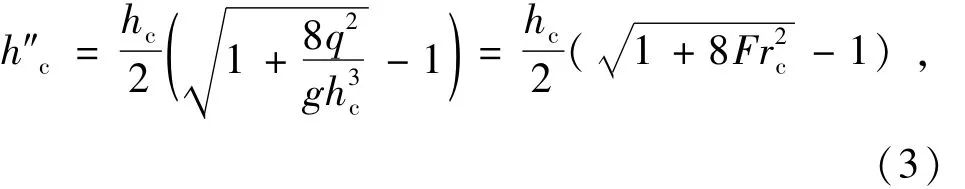
其中：Frc为跃前断面弗劳德数；hc为跃前水深，

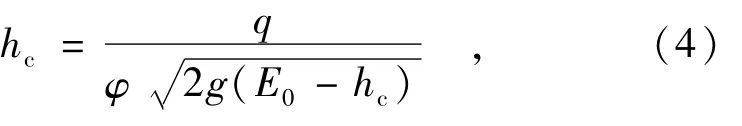
φ为流速系数。

消力坎的淹没系数σs决定于淹没程度hs／H10，其中hs＝ht－e。因为消力坎前有水跃存在，与一般实用堰前的水流状态不同，故淹没系数及淹没条件也有所不同。判别淹没出流的条件为

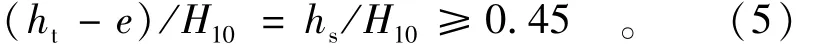
当hs／H10＜0．45时，消力坎为非淹没出流，σs＝1；当hs／H10＞0．45时，消力坎为淹没出流，σs＜1，其值可由表1前2列查得。

式（1）和式（2）即为消力坎式消力池的传统计算方法。可以看出，要计算坎高，必须知道淹没系数σs，才能求得堰上总水头H10和堰上水深H1，进而求得坎高e。但淹没系数又与堰上水头有关，所以计算过程一般用试算法。计算时先假定坎高，利用上述各式计算H1，H10，由表1查得淹没系数σs，校核单宽流量q值，直到与给定值相符为止。

2．2 淹没系数

2．2．1 淹没系数的研究成果

关于淹没系数，文献［6］根据表1的数据，拟合了一个方程，即

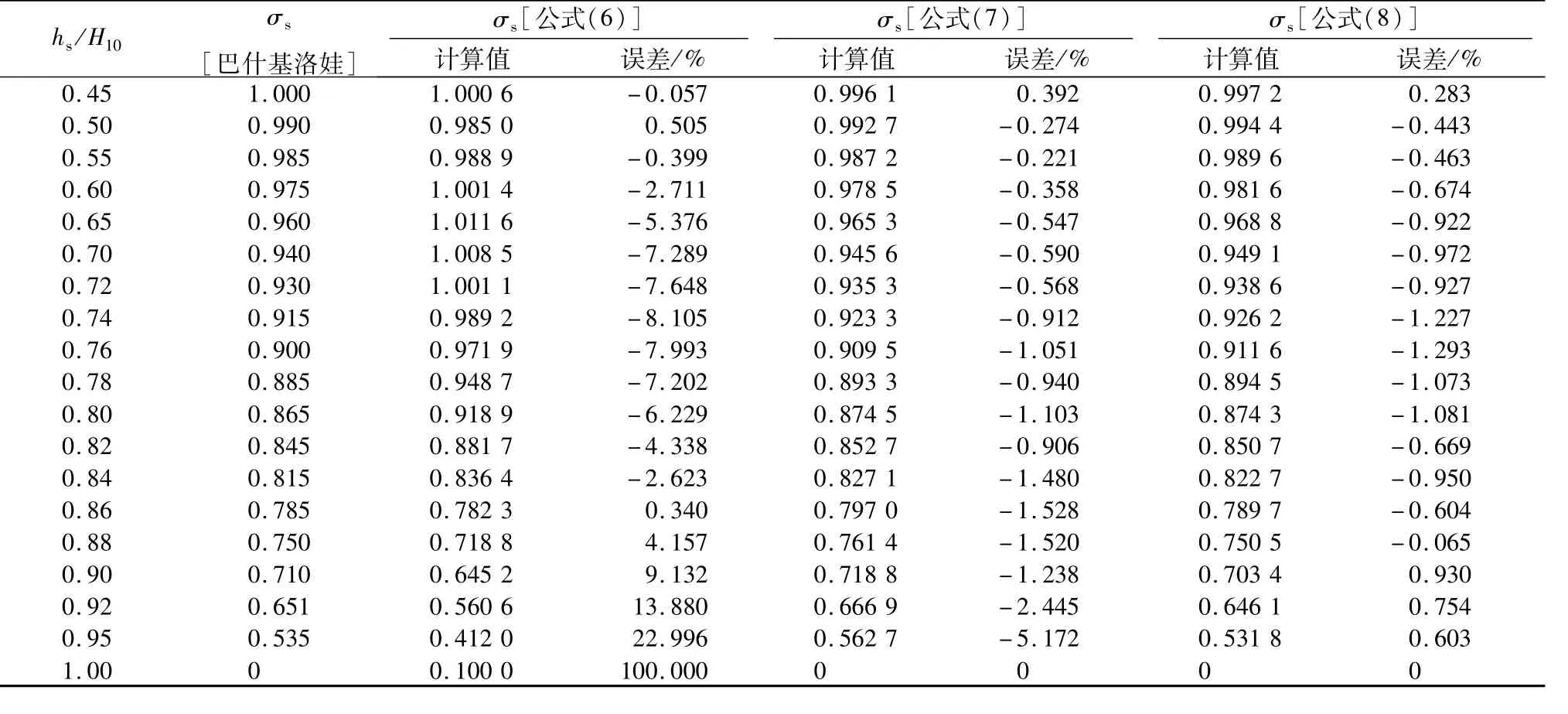
表1 消力坎淹没系数计算精度对照Table 1 Com parison of the calculation accuracy of subm ergence coefficient am ong different formu las

文献［12］给出了淹没系数的计算公式为

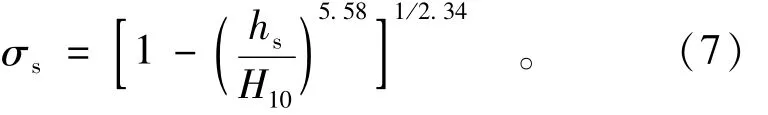
现将以上公式的精度进行比较，见表1。由表1中可以看出，式（7）的计算值与巴什基洛娃的试验值接近，而式（6）计算值与试验值相差较大。式（7）的相对误差虽然较小，但在高度淹没时，误差仍然较大，但式（7）的形式是合理的，因为在淹没度等于1时，淹没系数为零，而式（6）显然做不到这一点。现根据表中的数据重新拟合公式为

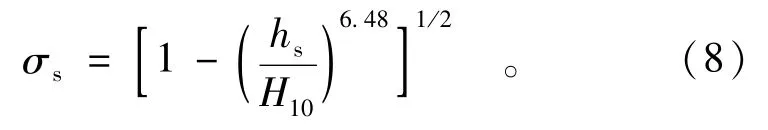
式（8）的最大误差仅为1．29%，尤其在高度淹没时误差没有超过1%。该公式精度高，所以本文采用式（8）计算淹没系数。

2．2．2 淹没系数的迭代公式及计算

由式（8）得

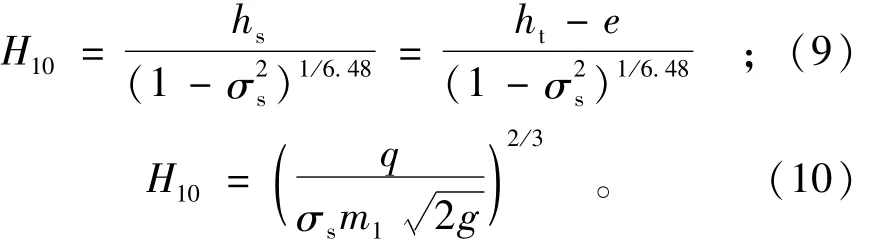
由以上2式得

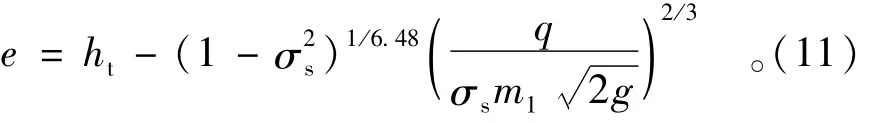
联立式（1）、式（2）和式（11）得淹没系数的迭代公式为

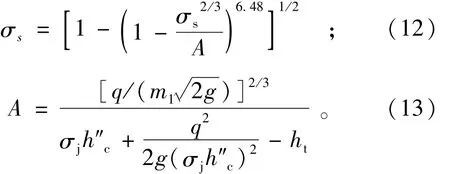
当单宽流量q、下游水深ht、跃后水深h″c及σj＝1．05～1．1和m1＝0．4～0．42一定时，A为常数。代入式（12）即可迭代出淹没系数σs，该式的初值可取为1，经验算，只需迭代5次即收敛。有了淹没系数，坎高可以用式（11）或式（1）、式（2）计算。

2．3 传统计算实例

某隧洞出口接扩散段，下接矩形消力池，如图2所示。已知护坦面以上总水头E0＝11．6 m，下游水深ht＝3．5 m，护坦段单宽流量q＝8．3 m3／（s·m），出口至消力池的流速系数φ＝0．95。试求：①判别下游水流衔接形式，是否设置消能设施；②如设置消力坎，求消力坎的高度。

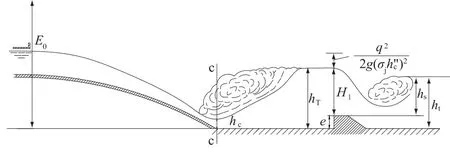
图2 某隧洞消力坎式消力池Fig．2 Sill-type stilling basin of a discharge tunnel

解：

（1）判别是否需要修消力池：

文献［4］用查表和试算法求得坎高为2．238 m，可见本文给出的消力坎高度和淹没系数的计算公式有足够的精度。

3 消力坎式消力池坎高简化计算

3．1 简化计算公式

可以利用梯形堰的受控水跃来计算消力坎式消力池的坎高，文献［5］给出了坎高的简化计算公式，但公式中未考虑水跃淹没系数σj和消力坎的淹没系数σs的影响，现考虑σj和σs，重新推导坎高的计算公式。由图1可以看出

由式（17）可以看出，消力坎式消力池的坎高是跃前断面弗劳德数Frc的函数。对于消力坎的自由出流，σs＝1，由上式可以直接计算出坎高e；对于淹没出流，仍须先求出消力坎的淹没系数σs，再由式（17）直接求出坎高e。

3．2 简化计算实例

仍采用2．3节的计算实例，由

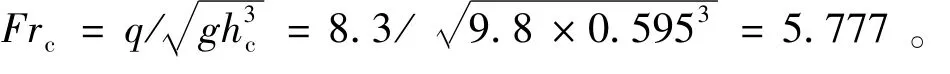
由公式（12）求淹没系数，2．3节算例已求得σs＝0．996 5，将Frc＝5．777和σs＝0．996 5代入式（17）得e＝2．237 m。可见，简化计算方法求得的坎高与传统方法计算得出的2．238 m基本一致。

4 消力坎的阻力系数

为了求得消力坎的阻力系数，设消力坎的阻力P为

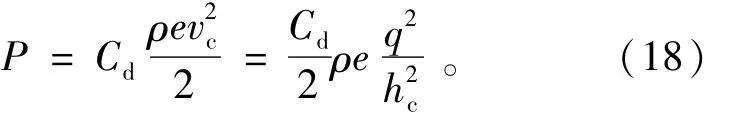
式中：ρ为水流的密度；vc为跃前断面的流速；Cd为阻力系数。

跃前断面和下游水深断面的动量方程为

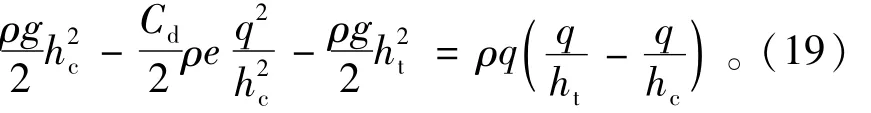
整理上式得

5 结 语

本文分析了消力坎式消力池淹没系数、坎高和消力坎阻力系数的计算方法。分析认为用式（12）计算消力坎的淹没系数有足够的精度，在此公式的基础上，得出了淹没系数的迭代公式。本文还利用梯形堰的受控水跃条件得出了消力坎高度的简化计算方法。由算例可以看出，本文提出的计算方法与传统方法的计算结果一致，说明公式准确、可靠。文中还导出了消力坎阻力系数的计算公式，为消力坎强度的设计提供了技术依据。

［1］ 肖兴斌．底流水跃消能在工程中的应用与发展述评［J］．人民珠江，1991，（3）：22－27．（XIAO Xing-bin．Application and Development of Underflow Hydraulic Jump Energy Dissipation in Engineering［J］．Pearl River，1991，（3）：22－27．（in Chinese））

［2］ 陈椿庭．高坝大流量泄洪建筑物［M］．北京：水利电力出版社，1988．（CHEN Chun-ting．Flood Discharge Structures of High Dam with Large Flow［M］．Beijing：Water Resources and Electric Power Press，1988．（in Chinese））

［3］ 吴持恭．水力学（下册）［M］．北京：高等教育出版社，1983．（WU Chi-gong．Hydraulics（Second Edition）［M］．Beijing：Higher Education Press，1983．（in Chinese））

［4］ 张志昌．水力学［M］．北京：中国水利水电出版社，2011．（ZHANG Zhi-chang．Hydraulics［M］．Beijing：China Water Power Press，2011．（in Chinese））

［5］ 郭子中．消能防冲原理与水力设计［M］．北京：科学出版社，1982．（GUO Zi-zhong．Energy Dissipation Principle and Hydraulic Design［M］．Beijing：Science Press，1982．（in Chinese））

［6］ 李鉴初，杨景芳．水力学教程［M］．北京：高等教育出版社，1995．（LI Jian-chu，YANG Jing-fang．Tutorial of Hydraulics［M］．Beijing：Higher Education Press，1995．（in Chinese））

［7］ 倪汉根，刘亚坤．击波、水跃、跌水、消能［M］．大连：大连理工大学出版社，2008．（NIHan-gen，LIU Ya-kun．Shock Wave，Hydraulic Jump，Plunge，and Energy Dissipation［M］．Dalian：Dalian University of Technology Press，2008．（in Chinese））

［8］ 谭振宏．消力池水力计算新法［J］．重庆交通学院学报，1990，9（4）：68－72．（TAN Zhen-hong．A New Method of Hydraulic Computation for Stilling Basin Design［J］．Journal of Chongqing Jiaotong University，1990，9（4）：68－72．（in Chinese））

［9］ 崔 忠，马铁成．浅议坎式消力池的水力计算［J］．广西水利水电，2011，（6）：26－30．（CUIZhong，MA Tiecheng．Discussion of Hydraulic Calculation for Sill-type Stilling Basin［J］．Guangxi Water Resources＆Hydropower Engineering，2011，（6）：26－30．（in Chinese））

［10］王永昌．底流消能水力计算［C］∥泄水工程与高速水流情报网第三届全网大会论文集，1990：261－270．（WANG Yong-chang．Hydraulic Calculation of the Underflow Energy Dissipation［C］∥Proceedings of the Third Conference of Drainage Engineering and High-speed Flow Information Network，1990：261－270．（in Chinese））

［11］马淑珠，宋怀兴．多级坎式消能池的水力设计［J］．东北水利水电，1996，（2）：15－26．（MA Shu-zhu，SONG Huai-xing．Hydraulic Design of Multi-level Sill-type of Stilling Basin［J］．Water Resource＆Hydropower of Northeast China，1996，（2）：15－26．（in Chinese））

［12］武永昌．消力池深（坎高）的迭代计算［J］．陕西水利，1987，（3）：28－33．（WU Yong-chang．Iterative Calculation on the Depth（Sill Height）of Stilling Basin［J］．ShannxiWater Resources，1987，（3）：28－33．（in Chinese））

［13］张怡霞，何志涛．铜街子溢流坝护坦消力坎设计［J］．水电站设计，1989，（3）：40－43．（ZHANG Yi-xia，HE Zhi-tao．Design of Apron Energy Dissipation Sill in the Tongjiezi Spillway［J］．Design of Hydroelectric Power Station，1989，（3）：40－43．（in Chinese））

［14］HABIBZADEH A，WU S，ADE F，et al．Exploratory Study of Submerged Hydraulic Jumps with Blocks［J］．Journal of Hydraulic Engineering，2011，137（6）：706－710．

［15］MANOOCHEHR FM，SADEGH H，BABAK L A，etal．Reduction of Stilling Basin Length with Tall End Sill［J］．Journal of Hydrodynamics，2011，23（4）：498－502．

［16］MOHAMED A N．Modeling of Free Jumps Downstream Symmetric and Asymmetric Expansions：Theoretical Analysis and Method of Stochastic Gradient Boosting［J］．Journal of Hydrodynamics，2010，22（1）：110－120．

（编辑：刘运飞）

Calculation of the Submergence Coefficient and the Sill Height of Sill-type Stilling Basin

ZHANG Zhi-chang，LIRuo-bing，ZHAO Ying，FU Ming-huan
（Institute ofWater Resources and Hydro-electric Engineering，Xi’an University of Technology，Xi’an 710048，China）

The simplified calculation methods for the submergence coefficient and the sill height of sill-type stilling basin are researched to substitute the traditional trialmethod．On the basis of previous researches，the iterative formula of submergence coefficient is derived through optimizing fitting，and the simplified calculation method of the sill height is analyzed．Furthermore，the drag coefficient of the sill is researched through momentum equation to provide technical support for its intensity design．The fitting and iterative formula of submergence coefficient，the simplified formula of sill heightand the formula of drag coefficient are put forward and verified correctby examples．The iterative and simplified formulas are simple in form，and avoid the complexity of trialmethod．

sill-type stilling basin；submergence coefficient；sill height；drag coefficient；iterative calculation

TV131．4

A

1001－5485（2013）11－0050－05

10．3969／j．issn．1001－5485．2013．11．011

2012－10－09；

2012－11－07

张志昌（1954－），男，陕西西安人，教授级高级工程师，主要从事水工水力学研究，（电话）13991942265（电子信箱）zhangzhichang1954＠163．com。