基于平均曲率模态和最小二乘支持向量机的混凝土拱坝损伤识别方法研究

李 波，刘明军，马奕仁，曹 浩，郭法旺

（1．长江科学院a．工程安全与灾害防治研究所；b．水利部水工程安全与病害防治工程技术研究中心；c．国家大坝安全工程技术研究中心，武汉 430010；2．中国电力投资集团公司南方分公司，广州 510130；3．长江工程监理咨询有限公司，武汉 430010；4．中国水电工程顾问集团贵阳勘测设计研究院，贵阳 550081）

基于平均曲率模态和最小二乘支持向量机的混凝土拱坝损伤识别方法研究

李 波1a，1b，1c，刘明军2，马奕仁3，曹 浩1a，1b，1c，郭法旺4

（1．长江科学院a．工程安全与灾害防治研究所；b．水利部水工程安全与病害防治工程技术研究中心；c．国家大坝安全工程技术研究中心，武汉 430010；2．中国电力投资集团公司南方分公司，广州 510130；
3．长江工程监理咨询有限公司，武汉 430010；4．中国水电工程顾问集团贵阳勘测设计研究院，贵阳 550081）

受众多外界因素的影响，混凝土拱坝结构损伤与模态信息之间表现出明显的非线性特征，这使得传统的模态分析很难精确识别结构的损伤程度。针对上述问题，提出一种基于平均曲率模态和最小二乘支持向量机的混凝土拱坝损伤识别方法。该方法在数值模拟的基础上，首先利用平均曲率模态对混凝土拱坝损伤位置进行识别，然后利用最小二乘支持向量机建立平均曲率模态和损伤程度间的非线性关系，对混凝土拱坝损伤程度进行识别。工程实例分析表明，该方法能有效地识别混凝土拱坝同时发生多处不同程度损伤的位置及损伤程度。

平均曲率模态；最小二乘支持向量机；混凝土拱坝；损伤识别

1 研究背景

近些年来我国制定了西部大开发战略和“西电东输”战略，大坝建设事业得到了前所未有的发展，尤其是锦屏（坝高305 m）、溪洛渡（坝高273 m）、小湾（坝高292m）、拉西瓦（坝高254m）等特高混凝土拱坝的建设，对国民经济作出了重大的贡献，产生巨大的经济效益。由于不利因素的影响，混凝土拱坝在服役期不可避免出现各种损伤，如果在该范围内没有观测点，现有的监测位移场、应力场和温度场变化的静态监测方法将不会监测到损伤的出现。这些损伤若不能及时发现，任其自由发展，将导致混凝土拱坝出现裂缝，危及大坝的安全。因此，对混凝土拱坝进行损伤识别成为亟待研究解决的一个重要课题。

损伤会使结构的刚度降低，进而导致其结构动力特性（如模态频率和振型等）发生变化。近年来，国内外许多专家学者对结构损伤识别进行了大量研究，并提出一系列基于模态分析的损伤识别方法，主要有基于固有频率、振型和曲率模态的损伤识别方法。基于固有频率的损伤识别方法主要通过损伤前后固有频率的变化识别结构的损伤状况，该方法理论基础清晰，测试简单方便，但是固有频率对结构早期损伤有时并不十分敏感，同时固有频率是结构的整体性能描述，很难识别损伤的确切位置。基于振型的损伤识别方法，通过分析损伤前后的振型变化情况来识别结构损伤，但是振型对局部损伤的位置和程度不敏感。曲率模态实质上是振型的二阶导数，可以通过各阶振型得到，大量研究表明，曲率模态比固有频率和振型对结构局部损伤更为敏感［1－2］。

混凝土拱坝受众多外界因素的影响，其结构损伤与模态信息之间表现出明显的非线性特征，这使得传统的基于模态分析识别结构损伤的方法遇到了困难，特别是对损伤程度的精确识别更是困难。人工神经网络的出现在一定程度上解决了上述问题［3－4］，然而，人工神经网络存在过拟合、收敛速度慢、易发散、易陷入局部极值等实际问题，这严重影响了它的实用性。支持向量机是在统计学习理论基础上发展起来的一种新的学习方法，它采用结构风险最小化原则，具有很强的泛化能力，并克服了神经网络中存在的过拟合、收敛速度慢、容易陷入局部极值等缺点，在损伤识别中有着很好的应用前景［5］。

针对上述问题，本文将模态分析技术与最小二乘支持向量机有机结合，提出基于平均曲率模态和最小二乘支持向量机的混凝土拱坝损伤识别方法。该方法在数值模拟的基础上，首先，利用平均曲率模态对局部损伤灵敏性高的优点，对混凝土拱坝损伤位置进行识别；然后，进一步利用最小二乘支持向量机泛化能力强的优点，建立平均曲率模态和损伤程度间的非线性关系，对混凝土拱坝损伤程度进行识别。

2 平均曲率模态方法

基于位移模态计算出的曲率模态，对于结构几何尺寸及工作性能的变化能够产生较明显的效果，以梁为例来讨论曲率模态的相关理论依据，其结论可以适用于任何类型的线性结构［6－7］。梁振动的微分方程为

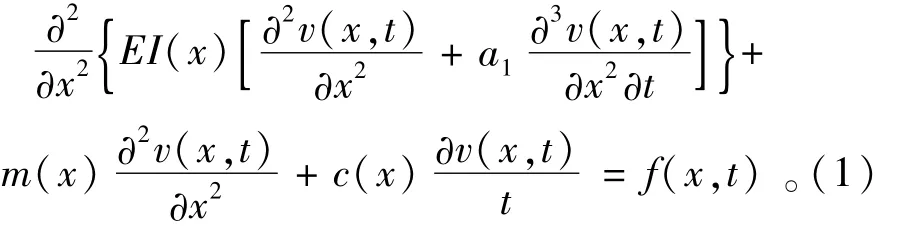
式中：E为梁的弹性模量；I（x）为梁的截面抵抗矩；v（x，t）为横向振动位移；a1为刚度比例因子；m（x），c（x）分别表示梁的质量和阻尼。

根据模态理论，方程（1）的解可以表示为模态贡献的叠加形式，即

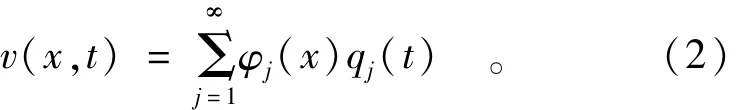
式中：j为模态阶数；φj（x），qj（t）分别为位移模态振型和模态坐标。

依据材料力学理论中弹性梁弯曲变形曲线曲率与位移的关系，任意截面x处梁弯曲振动曲线的曲率变化函数为

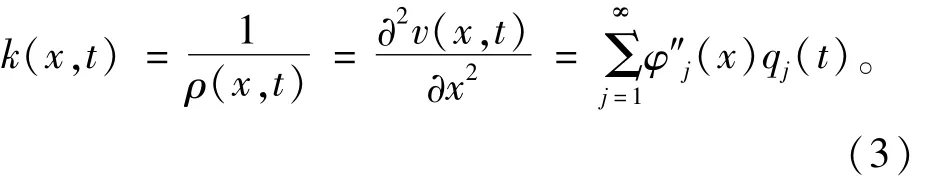
式中：φ″j（x）为梁的j阶曲率模态；k（x，t）为曲率；ρ（x，t）为曲率半径。

由材料力学知，梁的弯曲静力关系式为

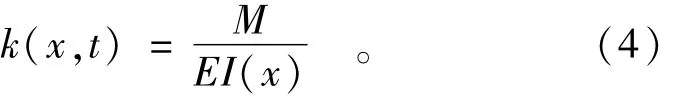
式中M为梁截面弯矩。

由式（3）和式（4）可知，曲率模态随结构刚度的变化而变化，即曲率模态对结构损伤敏感，而且曲率模态与位移模态是一一对应关系。

在模态分析中，通过频响函数可求解出结构的模态参数，然后在位移模态振型基础上按中心差分法近似计算曲率模态振型。当各节点之间距离相同时，第i个节点的第j阶曲率模态为

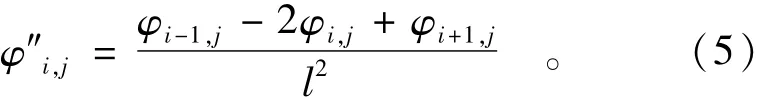
式中：φ″i，j为第j阶、第i个节点的曲率模态；l为各节点间的距离。

当节点间的距离不相同时，式（5）应作以下修正：

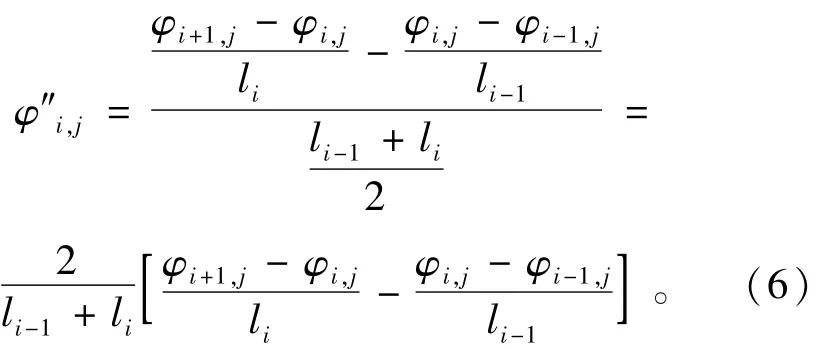
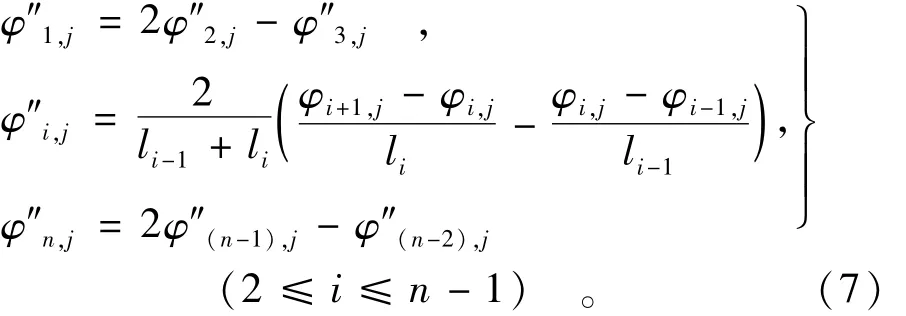
式中li为第i个节点与第i＋1个节点之间的距离。

第1个节点与最后1个节点的曲率模态无法通过式（6）算出，而它们不能简单设为0（只有当该点位于简支端或自由端的端点时，才可以作此处理），可以通过下式进行估算（假设共有n个测点）：

由模态振型衍生出来的曲率模态、曲率模态比、曲率模态差、平均曲率模态均可作为损伤因子。以下将重点分析平均曲率模态损伤因子（CDF），用下式表示为

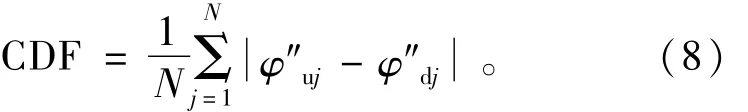
式中：N为所考虑的模态总数；φ″uj为无损结构的曲率模态；φ″dj为损伤结构的曲率模态。

3 最小二乘支持向量机

支持向量机克服了人工神经网络出现的问题，同时提高了计算效率。最小二乘支持向量机与标准支持向量机的主要区别在于采用不同的优化目标函数，并且用等式约束代替不等式约束，它是一种很有潜力的数据分类和回归工具［8－10］。已知一组训练集（x1，y1），…，（xl，yl），x∈Rn，y∈R对于非线性问题，可以通过非线性变换φ（·）将输入向量映射到高维特征空间，转化为类似的线性回归问题。最小二乘支持向量机利用结构风险最小化原则构造了下面的最小化目标函数：

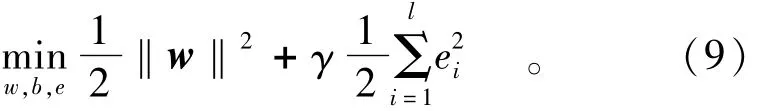
其中，w为权向量；γ为正则化参数；ei为样本训练误差。

同时将支持向量机算法中的不等式约束转化为等式约束，即

式中ai为Lagrange乘子。

根据优化条件：

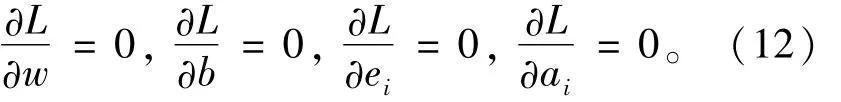
可以得到式（11）的最优条件：

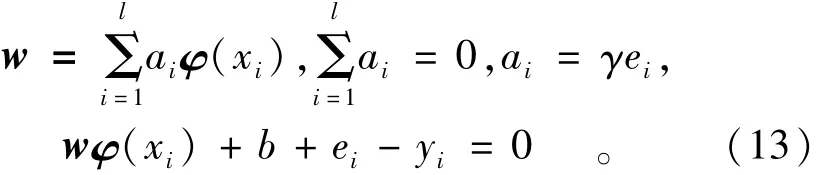
消去式（13）的w和e，可得

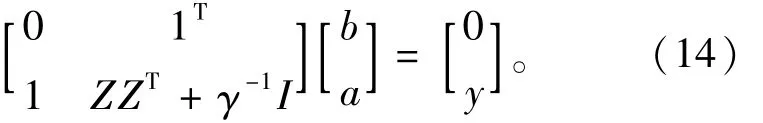
式中：y＝［y1，y2，…，yl］T，a＝［a1，a2，…，al］T，Z＝［φ（x1），φ（x2），…，φ（xl）］T，1＝［1，…，1］T。

解这个线性方程组求得b和a，最小二乘支持向量机回归函数为

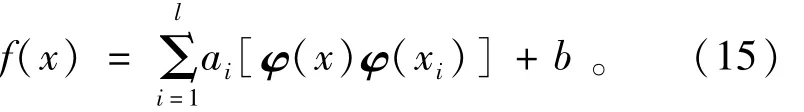
为了避免高维特征空间中的“维数灾难问题”，用输入空间的一个核函数K（x，xi）等效高维空间的内积形式，可以解决高维计算问题。所要求的回归函数为

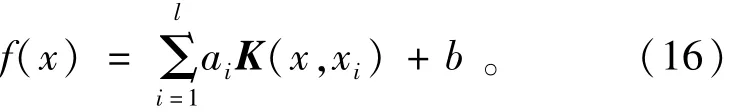
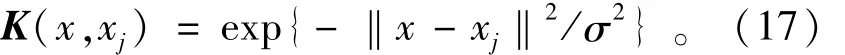
本文选择径向基核函数：采用径向基核函数的最小二乘支持向量机的主要参数是正则化参数和核函数宽度σ，这2个参数在很大程度上决定了最小二乘支持向量机的学习和泛化能力。常用网格搜索法来确定这2个参数。为了克服该方法计算量较大的缺点，本节采用改进的网格搜索法来确定参数，即先用一个大的步长进行粗糙的搜索，确定最好组合后，再在这个组合的周围用小的步长进行更精细的搜索，具体步骤如下：

（1）将γ和σ分别取M和N个值，组成M×N个γσ的组合。这里使用的参数范围是：γ∈［22，24，…，224］，σ∈［22，24，…，210］。

（2）对训练集归一化后，对步骤（1）中划分的组合采用交叉验证。为了提高训练的速度，在不影响模型精度的情况下，这里采用6折的交叉验证，求得最高的学习精度，得到最好参数组合。

（3）对步骤（2）中确定的参数正负22范围内，再以20．5为步长进行更精细的网格搜索，求得精度最高的参数组合。

相比一般的网格搜索法，改进的网格搜索法不仅可以减少训练量，而且可以提高模型的预测精度。

4 混凝土拱坝损伤识别步骤

混凝土拱坝损伤识别的具体步骤如下：

（1）根据实际资料，建立混凝土拱坝的三维有限元模型。

（2）使用MSC．Marc强大的动力分析求解功能，求解出混凝土拱坝损伤前后的各阶固有频率。将损伤前后的自振频率进行比较，初步判断混凝土拱坝是否存在损伤。

（3）求解出混凝土拱坝的损伤前后的各阶位移模态，利用上述介绍的曲率模态计算方法，计算出各种工况下的平均曲率模态，对混凝土拱坝的损伤位置进行识别。

（4）在已知损伤位置的情况下，计算出混凝土拱坝在所有可能损伤程度下的平均曲率模态。

（5）以损伤单元所属节点的平均曲率模态为最小二乘支持向量机的输入样本，实际损伤量为输出样本。

（6）结合改进的网格搜索法，利用最小二乘支持向量机进行训练和预测，识别出混凝土拱坝的损伤程度。

5 工程实例

某同心圆变半径的混凝土重力拱坝，自左向右有28个坝段，坝顶高程为126．3 m，最大坝高为76．3 m，坝顶弧长419 m，坝顶宽8 m，最大坝底宽53．5 m，有限元计算模型的范围：上下游方向取2倍左右坝高（各约150 m），左右坝肩各取约150 m。单元采用六面体8节点等参单元。模型共划分了9 471个单元，11 997个节点。如图1所示。

假定人工边界范围以内的坝基均是“无质量的弹簧”，在形成整个系统的特征矩阵时，坝基单元只考虑弹性，不考虑质量，以消除坝体在振动时形成的振动波的传递效应，避免人为的放大作用。坝体混凝土的泊松比和材料密度分别取为0．167和2 400 kg／m3，坝体和基岩的弹性模量分别为24．0 GPa和19．5 GPa。

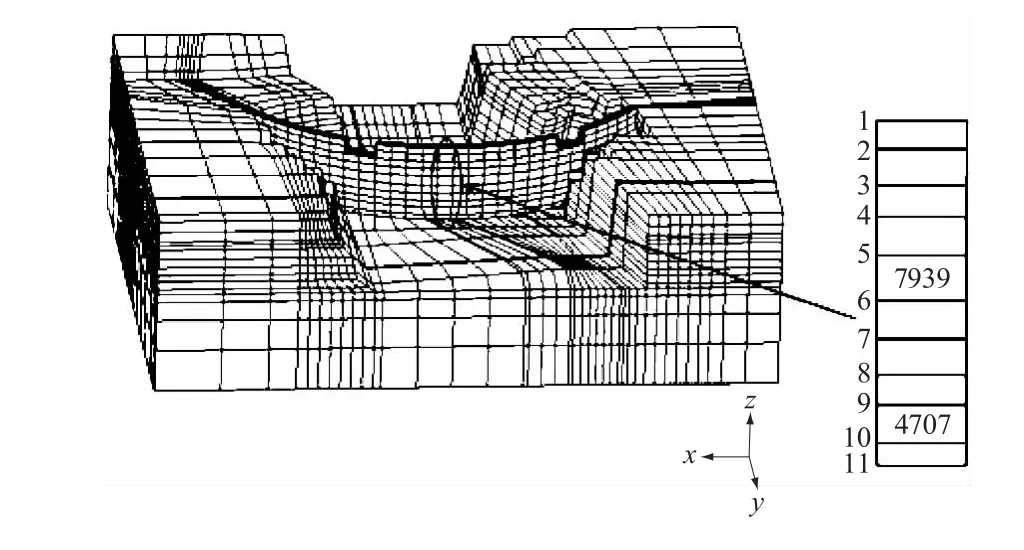
图1 混凝土拱坝有限元模型Fig．1 Finite elem entm odel of concrete arch dam

在坝基－坝体－库水的耦合系统中，假定坝基是无质量的弹性体，库水是不可压缩的，库水动水压力的影响按附加质量法考虑，折算为单位加速度相应的上游坝面结点附加质量，在对应结点上附加质量元。

5．1 损伤位置的识别

为了更清楚地描述损伤出现的位置，图1给出了大坝上游面关键单元和所属关键节点示意图，图中7939和4707为损伤单元的编号，1～11为关键节点的编号。为识别混凝土坝损伤的位置，本文在坝体的不同位置模拟了6种不同的损伤，详见表1。

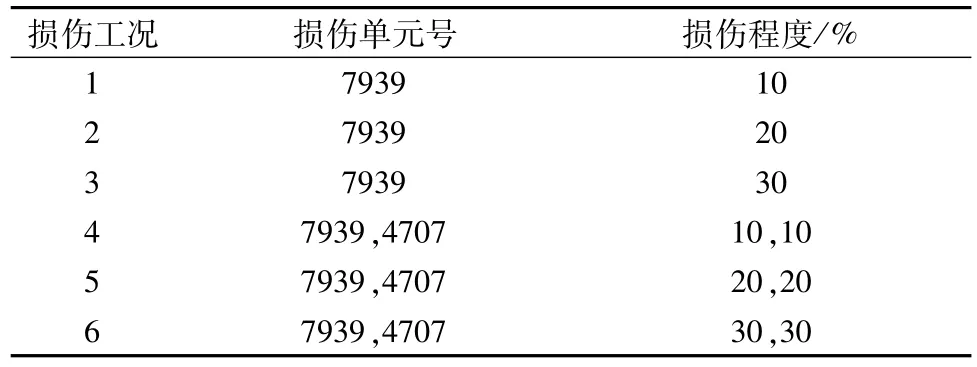
表1 单元损伤情况Table 1 Conditions of element damage

在正常蓄水位下，使用MSC．Marc强大的动力分析求解功能进行模态分析，各种损伤情况下，混凝土拱坝前4阶自振频率变化如表2所示。

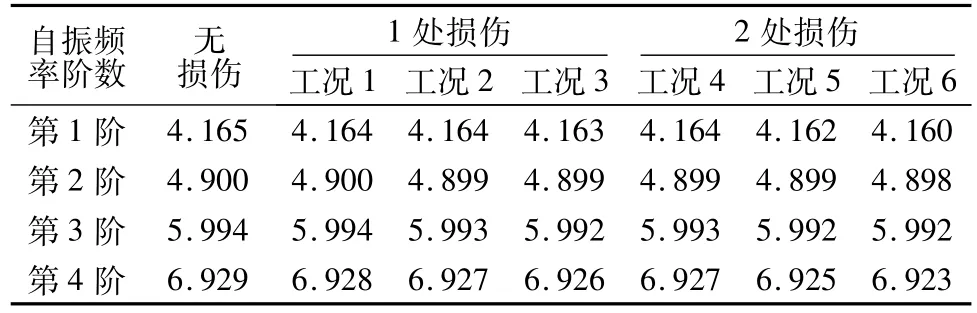
表2 各种损伤情况下的自振频率Table 2 Natural frequency in damage conditions

从表2中可以看出，在1处损伤和2处损伤下，模态自振频率值随损伤程度的加深而呈下降趋势，在理论上证实了刚度降低导致频率降低这一结论。但是变化的程度很小，实际测量中由于环境变化、噪音干扰等因素，很难识别混凝土拱坝的局部损伤。因此，以下采用平均曲率模态作为损伤因子对混凝土拱坝进行损伤识别。

图2为单元7939损伤前后各关键节点顺河向位移的前4阶平均曲率模态，图3为单元7939和4707损伤前后各关键节点顺河向位移的前4阶平均曲率模态。

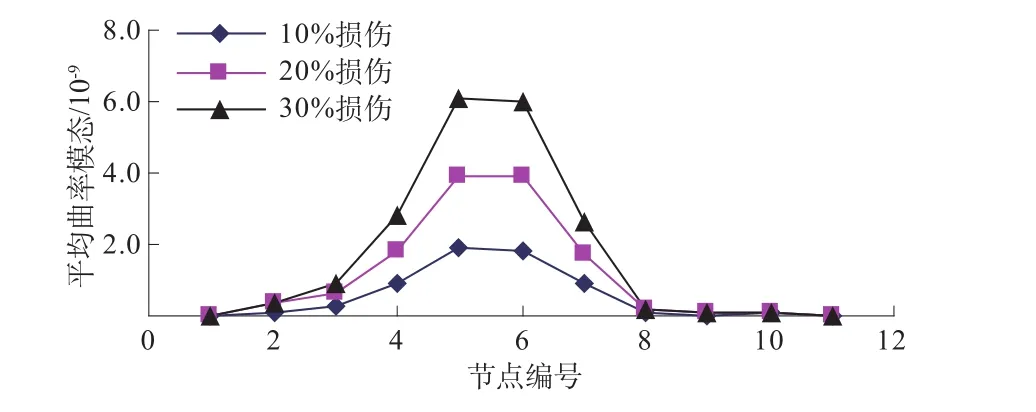
图2 1处损伤下平均曲率模态Fig．2 M ean curvaturemode in the presence of one damage

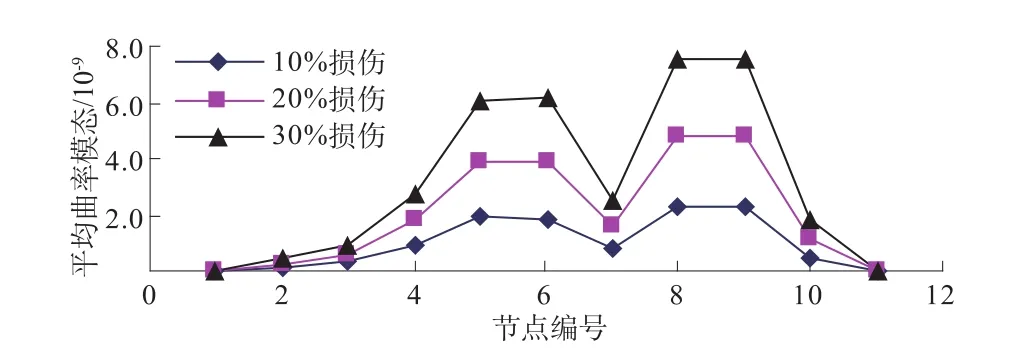
图3 2处损伤下平均曲率模态Fig．3 M ean curvaturemode in the presence of two damages

由图2和图3可以看出，在1处损伤和2处损伤下，损伤单元所属两节点的平均曲率模态损伤因子明显突变，并且随着损伤程度的增加，突变的程度增加。因此，平均曲率模态损伤因子可以有效地估计混凝土拱坝局部损伤的位置，并且可以定性分析损伤的程度。

5．2 损伤程度的识别

本文针对第5．1节中2处不同损伤进行研究。经过损伤位置分析可知混凝土单元7939和4707出现损伤，其所有可能的损伤程度为10%，20%，30%，构造2处损伤单元所有可能的损伤程度组合，并计算相应单元所属节点的平均曲率模态，各损伤单元训练样本为32＝9组。单元7939和4707的训练样本分别见表3和表4。结合改进的网格搜索法，利用最小二乘支持向量机进行训练，得到的最优参数组合（γ，σ）分别为（1 048 576，181．019 3）和（1 048 576，128），最终训练结果分别见表3和表4。

从表3和表4可看出，单元7939和4707的训练的相对残差绝对值很小，说明训练结果非常好。

在上述建立的最小二乘支持向量机模型基础上，对单元7939和4707分别出现15%和25%的损伤程度进行预测。预测结果分别见表5和表6，从表中可以看出，预测的相对残差绝对值都很小，说明

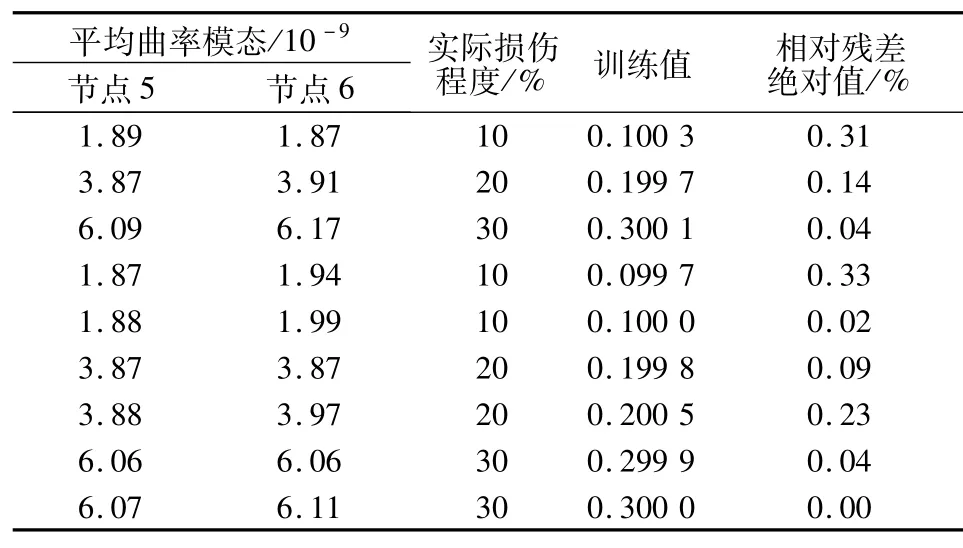
表3 单元7939的训练样本和训练结果Table 3 Training sam p les and results for element 7939

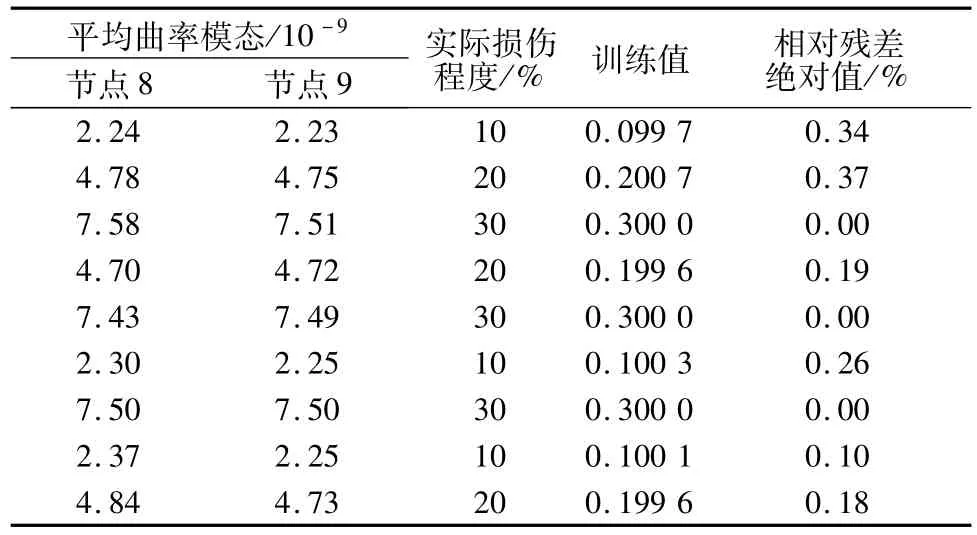
表4 单元4707的训练样本和训练结果Table 4 Training samp les and results for element 4707

表5 单元7939的预测样本和预测结果Table 5 Prediction sam ple and result for element 7939

表6 单元4707的预测样本和预测结果Table 6 Prediction sam p le and result for element 4707

建立的最小二乘支持向量机模型能有效地定量识别混凝土拱坝的损伤程度。

6 结 论

（1）混凝土拱坝模态自振频率随损伤程度的加深而呈下降趋势，但是变化的程度很小，实际测量中由于环境变化、噪音干扰等因素，很难识别混凝土拱坝的局部损伤。

（2）混凝土拱坝损伤处的前4阶的平均曲率模态会发生突变，且随着损伤程度的增大，突变程度也在增加。前4阶的平均曲率模态是一个对混凝土拱坝损伤比较敏感的参数，可用于对混凝土拱坝的多处损伤位置进行有效的识别。

（3）最小二乘支持向量机具有很强的泛化能力，将模态分析技术与最小二乘支持向量机有机结合，能有效地识别混凝土拱坝同时发生多处不同程度损伤的损伤位置和损伤程度。

［1］ 刘义伦，时圣鹏，廖 伟．利用曲率模态识别桥梁损伤的研究［J］．振动与冲击，2011，30（8）：77－81．（LIU Yi-lun，SHI Sheng-peng，LIAO Wei．Bridge Damage I-dentification Using Curvature Mode Shapes［J］．Journal of Vibration and Shock，2011，30（8）：77－81．（in Chinese））

［2］ 张 旭，葛继平，李胡生，等．基于曲率模态的箱梁损伤识别方法研究［J］．上海应用技术学院学报（自然科学版），2012，12（3）：201－206．（ZHANG Xu，GE Jiping，LI Hu-sheng，et al．Damage Identification of Box Beam Based on Curvature Theory Method［J］．Journal of Shanghai Institute of Technology（Natural Science），2012，12（3）：201－206．（in Chinese））

［3］ 李小荣，郭永刚．基于遗传算法优化神经网络权值的大坝结构损伤识别［J］．震灾防御技术，2008，3（2）：189－196．（LIXiao-rong，GUO Yong-gang．Dam Damage Identification on the Basis of Optimizing Neural Network Weight by Genetic Algorithm［J］．Technology for Earthquake Disaster Prevention，2008，3（2）：189－196．（in Chinese））

［4］ 于 菲，刁延松，佟显能，等．基于振型差值曲率与神经网络的海洋平台结构损伤识别研究［J］．振动与冲击，2011，30（10）：183－187．（YU Fei，DIAO Yan-song，TONG Xian-neng，et al．Damage Identification of an Offshore Platform Based on Curvature ofModal Shape Difference and BP Neural Network［J］．Journal of Vibration and Shock，2011，30（10）：183－187．（in Chinese））

［5］ 练继建，李松辉．基于支持向量机和模态参数识别的导墙结构损伤诊断研究［J］．水利学报，2008，39（6）：652－658．（LIAN Ji-jian，LISong-hui．Damage Diagnosis of Spillway Guide Wall Based on Support Vector Machine and Modal Parameter Identification［J］．Journal of Hydraulic Engineering，2008，39（6）：652－658．（in Chinese））

［6］ 马立英，周 ?A，彭晓俊．曲率模态及其在汽车后桥损伤识别中的应用［J］．同济大学学报（自然科学版），2011，39（8）：1208－1211．（MA Li-ying，ZHOU Hong，PENG Xiao-jun．Application of Curvature Mode Shape to Damage Identification of Rear Axle［J］．Journal of Tongji University（Natural Science），2011，39（8）：1208－1211．（in Chinese））

［7］ 张 静，静 行，袁海庆．基于曲率模态变化率指标的结构损伤识别［J］．华中科技大学学报（城市科学版），2010，27（2）：82－86．（ZHANG Jing，JING Hang，YUAN Hai-qing．Structural Damage Detection Based on Change Rate of Curvature Mode［J］．Journal of Huazhong University of Science and Technology（Urban Science），2010，27（2）：82－86．（in Chinese））

［8］ 李 波，顾冲时，李智录，等．基于偏最小二乘回归和最小二乘支持向量机的大坝渗流监控模型［J］．水利学报，2008，39（12）：1390－1394．（LIBo，GU Chongshi，LI Zhi-lu，et al．Monitoring Model for Dam Seepage Based on Partial Least Squares Regression and Least Square Support Vector Machine［J］．Journal of Hydraulic Engineering，2008，39（12）：1390－1394．（in Chinese））

［9］ 李 波，徐宝松，武金坤，等．基于最小二乘支持向量机的大坝力学参数反演［J］．岩土工程学报，2008，30（11）：1722－1725．（LIBo，XU Bao-song，WU Jin-kun，et al．Back Analysis of Dam Mechanical Parameters Based on Least Squares Support Vector Machine［J］．Chinese Journal of Geotechnical Engineering，2008，30（11）：1722－1725．（in Chinese））

［10］GU CS，LIB．Back Analysis ofMechanical Parameters of Roller Compacted Concrete Dam［J］．Science China：Technological Sciences，2010，53（3）：848－853．

（编辑：黄 玲）

Damage Identification of Concrete Arch Dam Using Mean Curvature Mode and Least Squares Support Vector Machine

LIBo1，LIU Ming-jun2，MA Yi-ren3，CAO Hao1，GUO Fa-wang4
（1．Yangtze River Scientific Research Institute，Wuhan 430010，China；2．South Branch of China Power Investment Corporation，Guangzhou 510130，China；3．Changjiang Project Supervision＆Consultant Company，Ltd．，Wuhan 430010，China；4．Hydrochina Guiyang Survey and Design Institute，Guiyang 550081，China）

Affected bymany external factors，the relation between concrete arch dam damage andmodal information is apparently nonlinear，whichmakes it difficult to accurately identify the degree of structural damage by traditional modal analysis．Aimed at these problems，amethod of identifying the damage of concrete arch dam by usingmean curvaturemode and least squares support vectormachine is proposed．On the basis of numerical simulation，the damage location is firstly identified usingmean curvaturemode，then the non-linear relationship betweenmean curvaturemode and damage degree is established using least squares support vectormachine to identify the damage degree．Engineering example shows that by using thismethod，the location and degree of various damages occurring simultaneously can be effectively identified．

mean curvaturemode；least squares support vectormachine；concrete arch dam；damage identification

TV312

A

1001－5485（2013）11－0113－06

10．3969／j．issn．1001－5485．2013．11．023

2013－09－10

“十二五”国家科技支撑计划项目（2012BAK10B04）

李 波（1980－），男，湖北天门人，博士，主要从事水工结构安全的研究，（电话）027－82926142（电子信箱）lb007403＠163．com。