复杂裂隙岩体力学特性的数值试验研究

蒋中明，伍东卫，赵海斌，冯树荣

（1．长沙理工大学a．水利学院；b．土木与建筑学院；c．水沙科学与水灾害防治湖南省重点实验室，长沙 410004；2．中南勘测设计研究院水能资源利用关键技术湖南省重点实验室，长沙 410014）

复杂裂隙岩体力学特性的数值试验研究

蒋中明1a，1c，伍东卫1b，赵海斌2，冯树荣2

（1．长沙理工大学a．水利学院；b．土木与建筑学院；c．水沙科学与水灾害防治湖南省重点实验室，长沙 410004；2．中南勘测设计研究院水能资源利用关键技术湖南省重点实验室，长沙 410014）

复杂结构面的模拟方法是裂隙岩体数值试验的关键技术之一。首先，利用ANSYS软件前处理功能和FLAC3D软件灵活的接触面生成功能，探索复杂裂隙岩体数值模型的构建方法；其次，利用数值试验方法对多结构面层状及柱状岩体的力学性质进行了单轴压缩研究，揭示了复杂层状及柱状岩体弹性模量及抗压强度的结构面倾角效应和尺寸效应，以及复杂岩体应力应变关系存在的差异性。数值试验结果表明，相同受力条件下结构面倾角的大小对裂隙岩体的变形特性有一定的影响，层状岩体或柱状岩体的单轴抗压强度及弹性模量会随试件尺寸的增大而变小并逐步趋向稳定。

裂隙岩体；数值试验；尺寸效应；结构面建模方法

1 研究背景

岩体在地质构造运动作用下，往往会形成规模不等、产状各异的节理或裂隙面［1］。这些结构面的存在，严重破坏了岩体的连续性和完整性，极大地弱化了岩体的力学性质和强度变形特征，给工程安全稳定带来隐患。为了全面认识复杂裂隙岩体的工程力学性质，国内外许多学者通过室内试验和现场原位试验，对复杂裂隙岩体的强度和变形特征进行了分析，研究了裂隙扩展、相互作用等对岩体强度和变形特性影响的基本规律［2－4］，提出了裂隙岩体强度及变形参数的取值方法［5－6］。目前，研究复杂裂隙岩体力学性质的方法大致有3种，即现场原位试验、室内试验、室内试验与数值计算相结合。通过原位试验研究复杂裂隙岩体的力学性质，所需原位岩体试件尺寸可能会有十余米或数米，这在大多情况下是不现实的，而且代价昂贵、条件困难。由于有代表性的岩体取样加工成试件比较困难，加上室内试验试件尺寸一般较小，因此将室内试验得到的试验成果进行延伸来推测一般情况下节理岩体的力学性质也存在较大的局限性。

近年来，国内外许多专家利用有限元、有限差分、离散元、边界元等数值计算方法对小尺寸或结构面分布较为简单的裂隙岩体力学参数、变形特性、强度取值、岩体REV等方面进行了研究［7－10］。但其研究成果的实用性有限，有些局限于小尺寸试件，有些仅进行二维平面变形研究等等。在实际工程中，裂隙规模大、分布复杂的岩体，要通过数值模拟的分析方法进行力学特性和强度变形特征的研究，就会存在着诸多问题。如：①单元数目过多而导致计算时间过长；②裂隙规模大小不一、分布复杂而难以模拟。

本文介绍了利用ANSYS软件进行前处理并结合FLAC3D软件灵活的接触面生成方法建立复杂裂隙岩体数学模型的全过程。运用此方法，通过对大量不同倾角、不同尺寸的层状岩体进行单轴压缩数值试验，得到了层状岩体抗压强度及弹性模量受结构面倾角、试件尺寸影响的基本规律，并与已有的研究成果进行了对比，论证本文研究成果的正确性。

2 复杂结构面模型生成方法

目前，无论是商业软件还是自编程序，都不能方便、快速地对包含多组且任意相交的结构面岩体进行有效地建模。为此，本文提出将ANSYS软件强大的前处理模块功能和FLAC3D结构面生成方法结合起来，完成含复杂结构面的岩体数值分析的建模方法，步骤如下：

（1）在ANSYS中生成不包括结构面的数值分析几何模型；

（2）利用APDL语言，通过循环语句，按照结构面的空间几何信息，通过变换工作面的位置，将完整几何模型进行分割，形成包含结构面信息的几何体；

（3）利用APDL语言，对切割后的复杂几何体进行材料自动分组；

（4）选择合适的单元类型对切割后的复杂几何体进行单元划分；

（5）将ANSYS生成的几何模型信息进行转换，形成FLAC3D软件所需的数值模型；

（6）利用FLAC3D中的FISH语言，将结构面上的节点进行分离处理，即在结构面的同一位置生成2个不同编号的节点；

（7）利用FISH语言中的循环语句，在不同分组单元之间完成任意复杂结构面的生成；

（8）利用FLAC3D中merge命令，将非结构面位置的分离节点进行合并，即可得到非贯穿性结构面。

按照上述步骤，构建2组正交结构面，贯穿、非贯穿结构面相对位置分别如图1所示。

图1 数值试验试件中的结构面Fig．1 Structural p lanes in the specim en for numerical test

3 层状岩体单轴压缩数值试验研究

在实际工程中，通常采用室内试验和现场试验来研究岩体的强度和变形特性。单轴压缩试验作为室内试验的重要部分，所得到的单轴抗压强度和弹性模量是岩石力学性质的重要参数。对于含多组及数量较多的岩体而言，室内试验受到试件制作等的影响，完全采用室内物理模型试验方法来研究结构面对岩体的力学性能的影响，存在很大的局限性。为此，下面采用本文提出的复杂岩体结构面生成方法，通过数值方法来研究层状岩体单轴抗压强度、弹性模量的尺寸效应和倾角效应等，以说明数值试验方法对包含复杂结构面的岩体性能研究的可行性。

3．1 数值试验模型

选取结构面倾角为0°，45°，90°的层状岩体试件进行单轴压缩数值试验。试件力学模型采用经典的摩尔库伦模型。根据单轴压缩试验原理，数值试验模拟轴向位移控制式加载过程。试件模型采用立方体，边长尺寸依次取1，2，4，8 m，结构面间距取0．5 m。运用本文建议的数模构建方法，构建的倾角45°、试件边长4 m的数值模型和结构面分布形态，如图2所示，其他尺寸与倾角的试件模型不再赘述。试件中结构面分布形态由结构面间距、结构面倾角、尺寸大小控制。数值计算参数的选取参照《工程岩体分级标准（GB 50218—94）》附录C中岩体及结构面物理力学参数取值范围，并结合淋溪河水电站坝址区岩石力学试验结果，拟定了岩块及结构面的力学参数，见表1、表2。

图2 岩体试件数值模型（边长为4 m，倾角为45°）Fig．2 M eshes of rock mass specimen（length＝4 m，dip angle＝45°）

表1 岩体力学参数Table 1 M echanical parameters of rock mass

表2 结构面力学参数Table 2 M echanical parameters of structural p lane

3．2 应力应变曲线分析

图3为层状岩体试件单轴压缩数值试验得到的应力应变曲线。由图3可知，尽管数值试件尺寸不同，但各数值试件的应力应变关系曲线变化规律基本一致。随着试件尺寸的加大，应力应变曲线趋于一致。此变化特征与安明［7］运用有限元数值试验技术所得结果基本一致。

由图3所示应力应变曲线可知，在其它条件相同、结构面倾角不同情况下，应力应变曲线总体特征相似，即当加载应变较小时，岩体应力应变关系表现为线弹性关系；随着加载应变的增加，岩体应力应变关系呈现出非线性变化的特点。由于结构面分布不同，各类试件非线性变化特征各异。

图3 岩体应力应变曲线Fig．3 Stress-strain curves of layered rock mass

结构面倾角为0°的岩体应力应变曲线可分为3个阶段：弹性阶段、塑性阶段、破坏阶段。

结构面倾角45°的岩体应力应变曲线没有明显的破坏阶段。倾角45°结构面试件在数值试验过程中因发生较大的剪切位移，应力应变曲线出现波动变化现象，这种现象可以理解为数值试件在试验过程中不断屈服，硬化的过程。

结构面倾角90°岩体应力应变曲线具有明显的弹塑性特征，试件在前期加载应变较小时，岩体变形特性受结构面影响较小，在加载后期，试件呈现明显的塑性变形，表明岩体受结构面影响较大。

3．3 抗压强度及弹性模量分析

3．3．1 岩体单轴抗压强度分析

表3为各类数值试件的岩体单轴抗压强度。表3中不同类型试件单轴抗压强度统计结果表明结构面倾角45°的层状岩体单轴抗压强度最小。此结论与何忠明［8］等利用相似材料制备的含不同倾角结构面的层状岩体试件单轴压缩试验得到的结果相同。

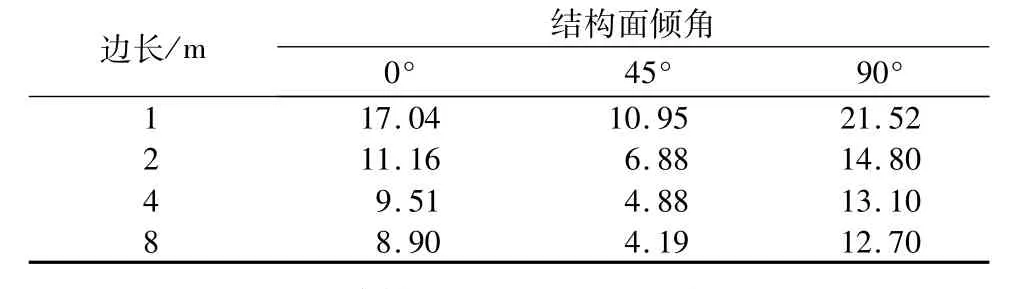
表3 试件单轴抗压强度统计Table 3 Uniaxial compressive strengths of the specimens MPa

表3还表明单轴抗压强度随试件尺寸的变化规律基本相同，即随试件尺寸的增加单轴抗压强度逐渐降低。但当试件尺寸增加到某一特征值后，岩体单轴抗压强度值趋于稳定，如图4所示。该结果与周莲君［9］运用实体单元模拟层状岩体所得的不同倾角结构面状况下圆柱形岩体试件抗压强度尺寸效应也一致。向文飞［10］利用Monte-Carlo方法在数值试件中生成二维随机裂隙，运用有限元法研究了单轴抗压强度随试件尺寸的变化特征，其结果与图4曲线变化特征也基本一致。

图4 单轴抗压强度的尺寸效应Fig．4 Size effect on the uniaxial compressive strength

3．3．2 岩体弹性模量分析

表4为数值试件的弹性模量统计表。试件弹性模量随尺寸的变化关系，如图5所示。弹性模量总体上随着倾角的加大而增大，但随数值试件尺寸的增大而减小。结构面倾角不同情况下，岩体弹性模量随试件尺寸变化的规律基本一致。

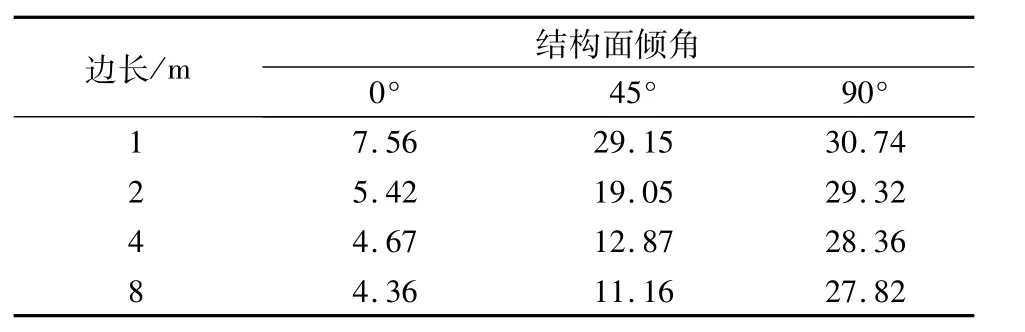
表4 试件弹性模量统计Table 4 Elastic m oduli of the specimens GPa

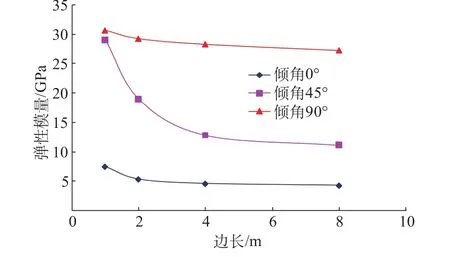
图5 岩体弹性模量尺寸效应Fig．5 Size effect on elastic modulus of rock mass

4 柱状岩体单轴压缩数值试验研究

为了进一步说明复杂岩体的力学特性的数值试验方法，选择具有更加复杂裂隙面构成的柱状岩体进行单轴压缩数值试验，数值模型和结构面分布形态如图6所示。

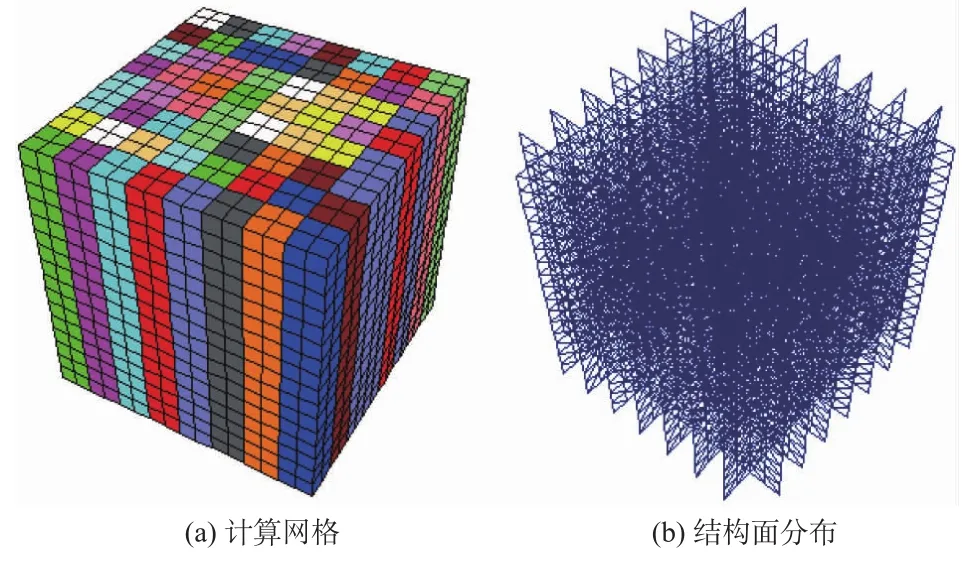
图6 柱状岩体试件数值模型（边长4 m）Fig．6 M eshes of columnar rock mass specimen（length＝4 m）

在相同试验条件下，分别对边长为1，2，4，8 m的柱状岩体试件进行单轴压缩数值试验，所得试件单轴抗压强度与弹性模量如表5所示。

表5 柱状岩体试件单轴压缩试验结果Table 5 Results of uniaxial com pressive test on specimens of columnar jointed rock mass

根据试验数据，绘制各类试件应力应变曲线如图7所示。图7表明不同尺度柱状岩体数值试件的应力应变关系曲线的变化规律基本相同：荷载较小时表现为弹性变形；荷载较大时，呈现出明显的弹塑性变形特性。图8为试件单轴抗压强度和弹性模量随试件尺寸变化而变化的关系图。由图可知，无论岩体中结构面分布如何变化，当岩体的尺度超过一定数值后，其强度和变形特性将趋于稳定。

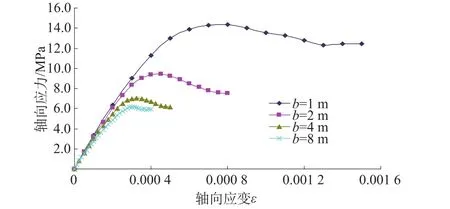
图7 柱状岩体试件应力应变关系Fig．7 Stress-strain curves of columnar jointed rock mass

5 结 语

本文研究了复杂裂隙分布状况下岩体的数值模拟方法，并利用此方法进行了含不同倾角结构面的层状岩体及柱状岩体的单轴压缩试验，数值分析结果表明，岩体中结构面的倾角大小对裂隙岩体的应力应变特性有一定的影响。无论是层状岩体还是柱状节理岩体，当岩体的尺度超过一定数值后，其强度和变形特性将趋于稳定。数值试验成果的合理性证明了本文提出的复杂裂隙结构面的建模方法能较好地解决复杂裂隙岩体的数值建模困难的问题，为进一步应用数值仿真手段研究复杂裂隙岩体的力学性质提供了基础。

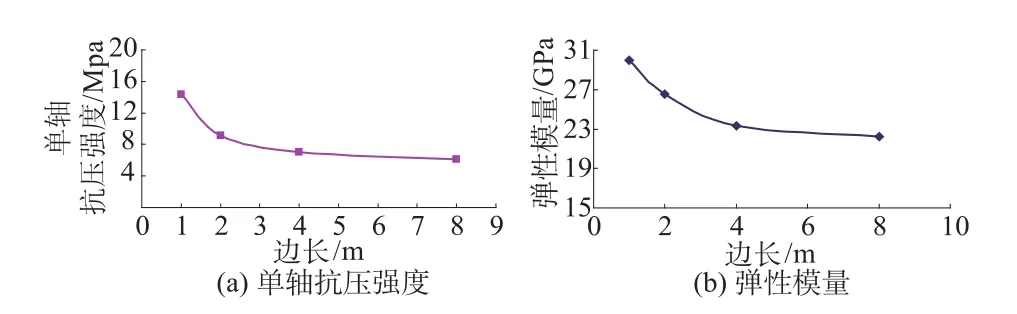
图8 柱状岩体单轴抗压强度、弹性模量尺寸效应Fig．8 Size effect on the uniaxial com pressive strength and elastic modulus of columnar rock m ass

［1］ 李德伦，王恩林，梁一鸿．构造地质学［M］．北京：地质出版社，1999．（LIDe-lun，WANG En-lin，LIANG Yihong．Structural Geology［M］．Beijing：Geological Publishing House，1999．（in Chinese））

［2］ 陈 新，廖志红，李德建．节理倾角及连通率对岩体强度、变形影响的单轴压缩试验研究［J］．岩土工程学报，2011，30（4）：781－789．（CHEN Xin，LIAO Zhihong，LIDe-jian．Experimental Study of Effects of Joint Inclination Angle and Connectivity Rate on Strength and Deformation Properties of Rock Massed under Uniaxial Compression［J］．Rock and Soil Mechanics，2011，30（4）：781－789．（in Chinese））

［3］ 王学滨．节理倾角对单节理岩样变形破坏影响的数值模拟［J］．四川大学学报，2006，38（2）：24－29．（WANG Xue-bin．Effect of Joint Inclination on Deformation and Failure of Rock Specimen with a Single Joint in Plane Strain Compression［J］．Journal of Sichuan University，2006，38（2）：24－29．（in Chinese））

［4］ 张志刚．节理岩体强度确定方法及其各向异性特征研究［D］．北京：北京交通大学，2007．（ZHANG Zhigang．Methods of Determining the Strength of Jointed Rock Mass and the Anisotropic Characters［D］．Beijing：Beijing Jiaotong University，2007．（in Chinese））

［5］ 王 毅，聂德新，张景科，等．岩体裂隙化程度与岩体变形参数的关系研究［J］．岩石力学与工程学报，2003，22（增2）：2572－2574．（WANG Yi，NIE De-xin，ZHANG Jing-ke，et al．Relation between Development Degree of Joints and Deformation Parameters of RockMass［J］．Chinese Journal of Rock Mechanics and Engineering，2003，22（Sup．2）：2572－2574．（in Chinese））

［6］ 李杭州，廖红建，冯夏庭，等．基于统一强度理论分析不连续面对岩体强度的影响［J］．岩土力学，2006，27（11）：1997－2000．（LI Hang-zhou，LIAO Hong-jian，FENG Xia-ting，etal．Analysis of Influence of Discontinuous Plane on Strength of Rock Mass Based on Unified Strength Theory［J］．Rock and SoilMechanics，2006，27（11）：1997－2000．（in Chinese））

［7］ 安 民，张红亮，尹小涛．基于数值实验的节理岩体变形特性尺寸效应［J］．武汉大学学报（工学版），2008，41（2）：73－77．（AN Min，ZHANG Hong-liang，YIN Xiao-tao．Scale Effect on Deformation Characteristics of Jointed Rock Mass Based on Numerical Test［J］．Engineering Journal ofWuhan University，2008，41（2）：73－77．（in Chinese））

［8］ 何忠明，彭振斌，曹 平，等．层状岩体单轴压缩试验分析与数值模拟［J］．中南大学学报（自然科学版），2010，41（5）：1906－1912．（HE Zhong-ming，PENG Zhen-bin，CAO Ping，et al．Test and Numerical Simulation for Stratified Rock Mass under Uniaxial Compression［J］．Journal of Central South University（Science and Technology），2010，41（5）：1906－1912．（in Chinese））

［9］ 周莲君，彭振斌，何忠明，等．层状岩体压缩强度尺寸效应的数值分析［J］．工业建筑，2009，39（5）：81－83．（ZHOU Lian-jun，PENG Zhen-bin，HE Zhong-ming，et al．Numerical Analysis for Size Effect of Stratified Rock Mass under Compression［J］．Industrial Construction，2009，39（5）：81－83．（in Chinese））

［10］向文飞．裂隙岩体表征单元体及力学特性尺寸效应研究［D］．武汉：武汉大学，2005．（XIANGWen-fei．Representative Elementary Volume of Fractured Rock Masses and the Size Effect of Mechanical Properties［D］．Wuhan：Wuhan University，2005．（in Chinese） ）

（编辑：姜小兰）

Numerical Test on Mechanical Behavior of Complicated Fractured Rock Mass

JIANG Zhong-ming1，3，WU Dong-wei2，ZHAO Hai-bin4，FENG Shu-rong4
（1．School of Hydraulic Engineering，Changsha University of Science＆Technology，Changsha 410004，China；2．School of Civil Engineering and Architecture，Changsha University of Science＆Technology，Changsha 410004，China；3．Key Laboratory ofWater-Sediment Sciences and Water Disaster Prevention of Hunan Province，Changsha University of Science＆Technology，Changsha 410004，China；4．Hunan Provincial Key Laboratory of Key Technologies for Water Power Resource Utilization，Zhongnan Engineering Corporation，Changsha 410014，China）

Themodeling of complex structural planes in rock mass is a key technique in the numerical test of fractured rock mass．A numericalmodel for the structural planes in rock mass is established bymeans of the pre-processing of ANSYS software and the flexible interface generation of FLAC3Dsoftware．Themodel is employed to numerically simulate themechanical behaviors of layered and columnar rockmasseswith complex structural planes under uniaxial compression．The regularity of structural plane’s dip angle and specimen’s size respectively affecting the elasticmodulus and compression strength of layered and columnar rock mass is obtained．The relations between stress and strain of different rockmasses are different．The result also shows that under the same stress，the dip angle of structural plane has influence on the deformation behavior of fractured rock mass．The uniaxial compressive strength and elasticmodulus of layered and columnar rock mass decrease and then gradually stabilize with the increase of specimen size．

fractured rock mass；numerical test；size effect；numericalmodeling of structural plane simulation

TU443

A

1001－5485（2013）11－0072－05

10．3969／j．issn．1001－5485．2013．11．014

2012－09－26；

2012－11－18

湖南省自然科学基金（12JJ3055）；中国水电顾问集团科技计划项目（2010680）

蒋中明（1969－），男，重庆市人，教授，博士，主要从事水工结构及岩土工程研究工作，（电话）13975821515（电子信箱）zzmmjiang＠163．com。