图像多模态扰动的人脸识别方法

张国庆，王正群，王颖静，徐 伟

ZHANG Guoqing1，2,WANG Zhengqun2,WANG Yingjing2,XU Wei2

1.南京理工大学 计算机科学与工程学院，南京 210094

2.扬州大学，信息工程学院，江苏 扬州 225127

图像多模态扰动的人脸识别方法

张国庆1，2，王正群2，王颖静2，徐 伟2

ZHANG Guoqing1，2,WANG Zhengqun2,WANG Yingjing2,XU Wei2

1.南京理工大学 计算机科学与工程学院，南京 210094

2.扬州大学，信息工程学院，江苏 扬州 225127

为了克服因人脸图像检测引起的配准不稳定性和小样本引起的维数灾难，由一副二维人脸图像通过上下左右平移生成4个图像，把生成的图像与原来的图像一起加入训练样本集，构成新的训练图像集。基于二维图像，结合图像局部结构信息，设计了准则函数，获得双投影矩阵，抽取人脸特征。对待识别人脸图像，由它的扰动图像设计识别方法。与传统的人脸识别方法相比，该方法的识别效果更好；Yale和ORL人脸数据库上的实验结果验证了该方法的有效性。

二维线性判别分析（2DLDA）；小样本问题；图像扰动；特征抽取

1 引言

特征提取主要达到两个方面的目的：一是寻找针对模式最具鉴别性的描述，以使此类模式的特征能最大限度地区别彼类;二是在适当的情况下实现模式的数据描述的维数压缩。特征提取成为人脸识别最基本的问题之一，提取有效的鉴别特征是解决该问题的关键。

在人脸特征提取技术的发展过程中，人脸图像的向量表示方法一直占据着重要的地位。在这些方法中，主成分分析PCA[1]、线性判别分析LDA[2]、局部保持投影LPP[3]是代表性的特征提取方法，它们将高维向量空间的图像X映射到低维向量空间的图像Y，即求出变换矩阵A，满足投影方程Y=ATX。A中的向量分别称为Eigenfaces[1]、Fishefaces[2]和Lapfcianfaces[4]。但是，二维图像本身是矩阵形式的数据，基于向量子空间的特征提取方法均需将矩阵转化为向量后才能处理，而这种转化破坏了图像像素之间的空间关系，容易造成图像局部空间信息的损失，图像自身所包含的信息绝不是向量的表示形式可以完全替代的，而且转换后的向量维数一般过高，给特征提取带来很大的困难，极易造成“小样本问题”的出现，增加算法的复杂度。

正是由于以上的原因，促使子空间特征提取方法寻找新的数据表示形式，因而基于图像自身表现形式的子空间方法得到发展，从而扩大了许多已有算法的使用范围，使其不仅仅局限于向量空间。Yang等人首先将图像矩阵的思想引入到主成分分析，提出了有名的二维主成分分析（Two-Dimensional Principle Component Analysis，2DPCA）[5]，直接对二维图像矩阵提取特征。2DPCA使用图像矩阵计算协方差，最佳投影方向由对应协方差矩阵的最大特征值集的正交特征向量集构成，明显缩短了特征提取的时间，取得了更好的识别率。随后Ye等人提出了图像矩阵的低秩分解算法（Generalized Low Rank Approximation Matrix，GLRAM）[6]，寻找左乘和右乘的两个正交矩阵，使投影后特征矩阵有最大协方差。

Ye又提出了二维线性判别分析（Two-Dimensional Linear Discriminate Analysis，2DLDA）[7]，直接使用图像矩阵构建类内散度矩阵和类间散度矩阵。这些基于二维图像矩阵的方法直接在图像矩阵上计算协方差或散度矩阵，所得矩阵的维数等于图像的行数和列数，计算起来简单方便。另外，矩阵投影到每个特征向量得到一个向量，而不是一个单独的值，这样获得的特征个数多于基于向量的方法。

2DPCA和2DLDA都注重在欧氏空间中保持流形的全局结构，而忽视了流形的局部结构，类似算法[8-9]往往注重单一目标，而忽视了整体考虑。TSA致力于保持流形的局部几何结构，可是忽视了流形的全局判别结构，尤其是对判别信息没有充分利用，算法仍然存在提高性能的潜力。

文献[10]提出了二维局部敏感判别分析（Two-Dimensional Locality Sensitive Discriminate Analysis，2DLSDA），它是局部敏感判别分析（Locality Sensitive Discriminate Analysis，LSDA）[11]的推广算法，把基于向量的LSDA算法推广应用到图像矩阵，但是2DLSDA的变换矩阵增加了过多的约束，算法的内涵没有完全挖掘出来。

本文提出一种二维图像扰动的人脸识别方法（Two-Dimensional Disturbing Face Recognition，2DDFC）。由一副二维人脸图像通过上下左右平移生成4个图像，把生成的图像与原来的图像一起加入训练样本集，构成新的训练图像集。基于二维图像，结合图像局部结构信息，设计准则函数，获得双投影矩阵。该方法一定程度上消除了小样本问题，扩大了人脸图像表示的多样性，并且有利于克服因位移带来的图像不稳定性。算法保持了流形的局部几何结构和流形判别结构，划分了类内和类间的类别信息，并且根据数据样本的类别信息分别构建类内和类间紧邻图。由图像的扰动，设计了人脸图像识别方法；在Yale和ORL人脸数据库上的实验结果验证了该人脸识别方法的有效性和鲁棒性。

2 多模态扰动的人脸识别方法

2.1 二维局部判别分析（2DLDA）

因为2DPCA没有利用样本的类别信息，不能保证得到的投影向量是分类意义上最优的。2DLDA[9]利用了类别信息，算法对分类更加有利。2DPCA只是重视图像矩阵的行的相关性，忽视了列的相关性；而2DLDA既重视行的相关性，也重视列的相关性，实现了从行和列两个方向对图像信息进行压缩。

设有图像样本 Xi∈Rm×n(i=1，2，…，N)，样本的类别数目为l，类别分别为C1，C2，…，Cl，类别Ci共有ni个样本图像。设为Ci类的样本均值矩阵，i=为全局样本均值矩阵。

2DLDA算法寻找两个变换矩阵P和Q，满足P∈Rm×k, Q∈Rn×l,将图像矩阵 Xi映射为Yi∈Rk×l(i=1，2，…，N)，满足方程Yi=PTXiQ。

原始图像经过变换矩阵P和Q的映射后，在低维空间中类内距离的平方Dw和类间距离的平方DB可以表示为：

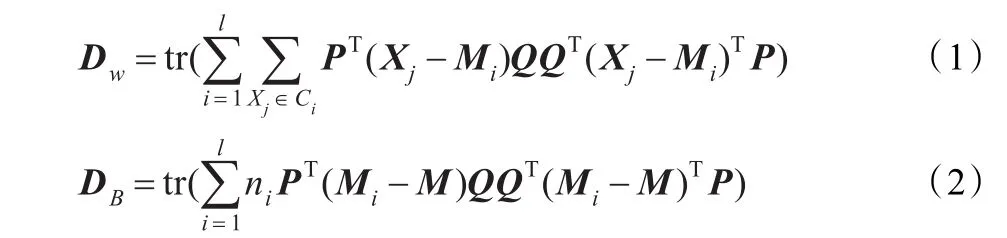
那么，2DLDA的优化问题为：

从上式可以看出，最优化转换矩阵P和Q即在最大化DB的同时最小化Dw。

2.2 人脸图像扰动和特征抽取

设有图像样本Xi(1，2，…，N)∈Rm×n，X=[X1，X2，…，XN]，对每副图像 Xi作相应扰动。取 Xi1=[Xi-1，j]（行方向左移一个像素），Xi2=[Xi+1，j]（行方向右移一个像素），Xi3=[Xi，j-1]（列方向上移一个像素），Xi4=[Xi，j+1]（行方向下移一个像素），在移动时，行列不足部分由0像素值补足，生成后4个图像后，包括Xi共5幅图像，它们的外围行列像素全部去掉。由 Xij(j=1，2，3，4)和 Xi（重新表示为 Xi0）构成新的训练图像集：X′=[X10，X11，X12，X13，X14，…，Xi0，Xi1，…]，X′共有5N个样本，寻找m×k的转换矩阵P和n×l的转换矩阵Q，使得映射满足Y=PTXQ。

因为人脸图像空间可以看做是嵌入高维图像空间中的非线性子流形M，通过M上的散点可以估计它的全局和局部特征，为此构造类内图Gw和类间图GB，并对二者进行数学建模。 Xij(i=1，2，…，N，j=0，1，…，4)是 M 上

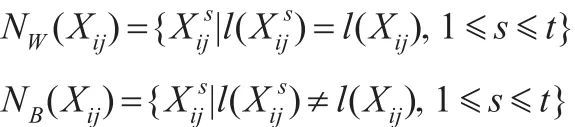
定义Gw的权重矩阵SW和GB的权重矩阵SB。

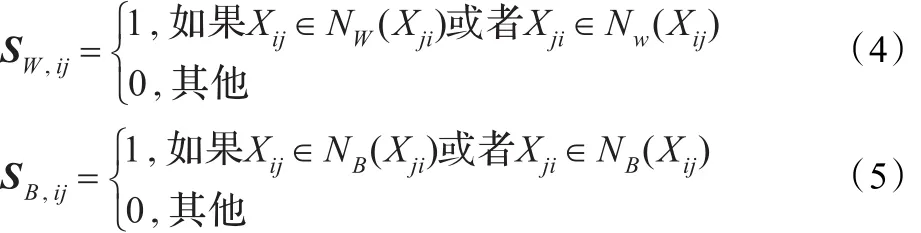
SW，ij和SB，ij分别表示SW和SB第i行和第 j列的元素。

假设Xi和Xj在子空间的映射分别为Yi和Yj。如果Xi和 Xj相距很近且具有相同类别标记，Yi和Yj应相距很近；如果 Xi和Xj相距很近但具有不同类别标记，Yi和Yj应相距很远。根据上述思想，为了获得投影变换矩阵P、Q，同时解如下优化问题：

至此，同时优化式（6）、（7）问题可以转化为求P、Q，使得tr(PTSWQP)和tr(PT(DBQ-SBQ)P)同时最大，且满足约束tr(PTDWQP)=1。

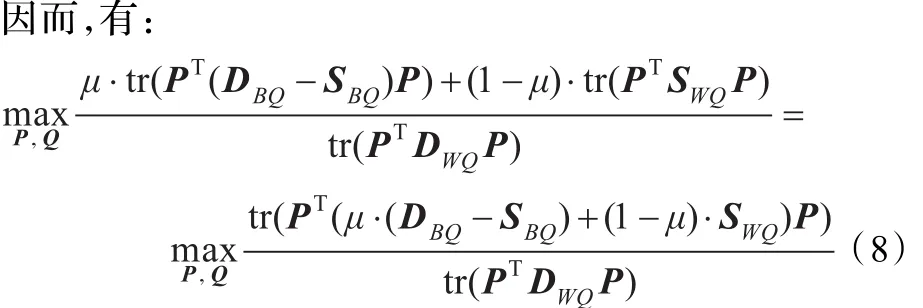
其中，μ是合适的调节参数，且满足0≤μ≤1。

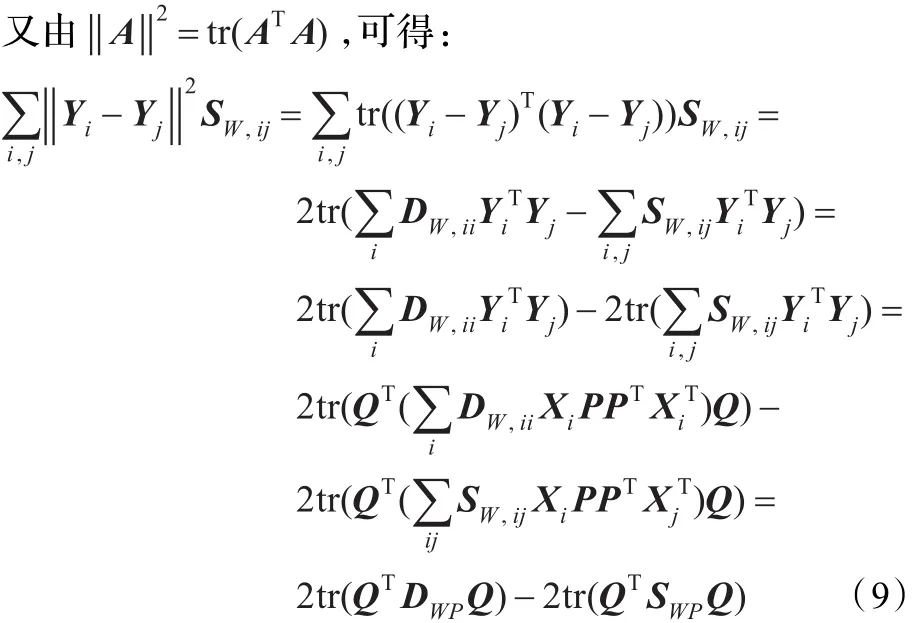
同理：由式（6）知，优化问题可以转化为

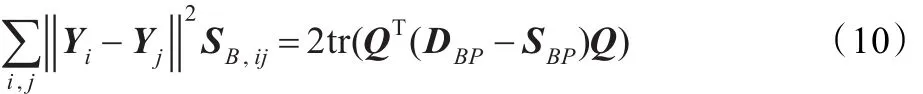
由式（6）和（7）知，优化问题可以转化为tr(QTSWPQ)和tr(QT(DBP-SBP)Q)同时最大，且约束 tr(QTDWPQ)=1。因而有：

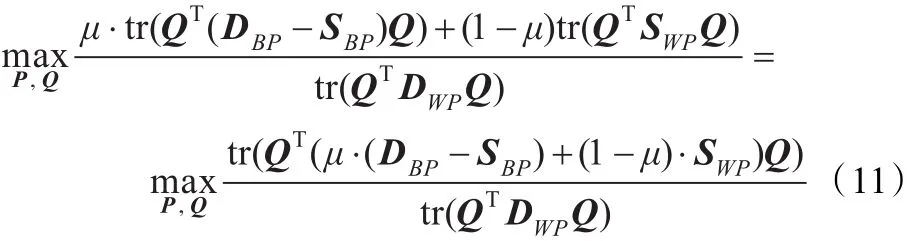
由式（8）和（11）知，P是(μ·(DBQ-SBQ)+(1-μ)·SWQ，DWQ)的广义特征向量矩阵，Q是 (μ·(DBP-SBP)+(1-μ)·SWP，DWQ)的广义特向量矩阵。直接计算P和Q比较困难，根据文献[9]的迭代计算方法，首先令 P为单位矩阵，由式（12）解出广义特征向量矩阵Q：

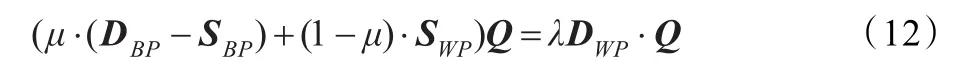
解出Q后，由式（13）解出广义特征向量矩阵P并使它得到更新：然后按照设定的迭代次数计算得到最后的P和Q。

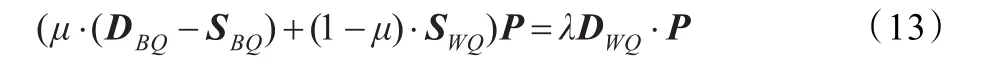
算法

步骤1由一副人脸图像X通过上下左右平移一个像素，构造成另外四副图像Xi(1，2，3，4)。

步骤2把Xi(1，2，3，4)）与X一起加入训练图像集，构成新的训练图像集。

步骤3构造类内图GB和类间图GW。

步骤4计算广义特征向量矩阵P和Q。

2.3 人脸图像扰动和识别

3 实验结果与分析

为了验证本文算法的有效性，采用YALE和ORL人脸数据库进行实验测试，将本文算法与LDA、二维线性判别分析（2DLDA）进行比较；设置参数μ=0.1。由训练样本图像计算得到人脸的张量子空间，将测试样本图像投影到张量子空间中，用最近邻分类器进行分类识别。

3.1 实验1与分析

ORL库包含40个人，每个人10幅图像，图像的分辨率为112×92，这些图像有些拍摄于不同时期；人脸脸部表情与脸部细节有变化，例如：笑或不笑，睁眼或闭眼，带与不带眼镜；人脸姿态有变化，旋转可达20°；人脸尺度也有最多10%的变化。

实验中，选择每个人的第1、3、5、7共4幅图像作为训练样本，其余6幅图像作为测试样本。训练过程近邻对数K取为30。选取5到60个投影轴进行特征抽取，比较LDA、2DLDA和本文方法在最近邻分类器下的分类识别效果。图1描述了这几种方法在ORL人脸库上的识别性能；表1描述了这几种方法在ORL人脸库上的最大识别率。

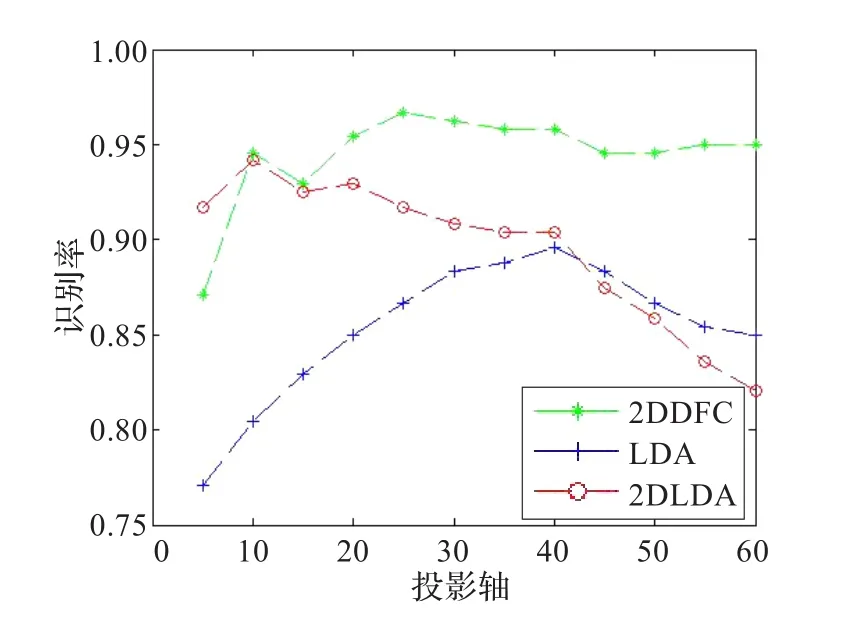
图1 最近邻分类器下LDA、2DLDA和本文方法在ORL库上的性能比较

表1 LDA、2DLDA和本文方法在ORL人脸库上的最大识别率比较

由图1可以看到，本文方法在最近邻离分类器下的识别性能明显优于LDA、2DLDA，并且随着投影轴数的增多，本文方法的性能会逐渐提高。

由表1可以看到，本文方法在投影轴为25时识别率最大，且都超过了其他两种方法的最好识别率。

3.2 实验2与分析

Yale人脸图像库包括15个人，每人11幅图像构成。这11幅图像分别为正常光照条件下，是否戴眼镜，不同光源，不同表情下的图像。每幅图像的分辨率为100×80。

实验中，选择每个人的后6幅图像作为训练样本，前5幅图像作为测试样本。训练过程近邻参数K取为5。选取5到60个投影轴进行特征抽取，比较LDA、2DLDA和本文方法在最近邻分类器下分类识别效果。图2描述了最近邻分类器下这几种方法在Yale人脸库上的识别效果；表2描述了这几种方法在Yale人脸库上的最大识别率。

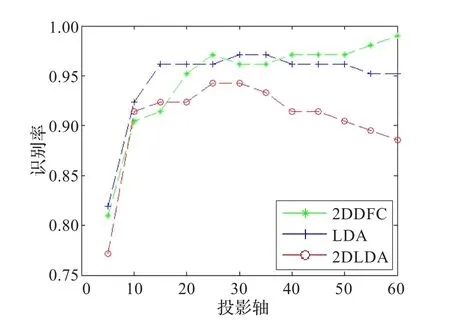
图2 最近邻分类器下LDA、2DLDA和本文方法在Yale库上的性能比较

表2 LDA、2DLDA和本文方法在Yale人脸库上的最大识别率比较

由图2可以看到，本文方法在最近邻分类器下的识别性能明显优于LDA、2DLDA。当投影轴数达到40到60的阶段时，识别率趋于稳定且达到最大值。

由表2可以看到，本文方法在投影轴为60时识别率为99.03%，且都超过了其他两种方法；特别是，与基于二维图像信息的人脸识别算法2DLDA相比，识别性能得到很大提升。

4 结论

提出了一种二维图像扰动的人脸识别方法2DDFC，该方法由特征抽取和识别两部分构成。由一副人脸图像生成4个图像，把生成的图像与原来的图像一起加入训练样本集，构成新的训练图像集。基于二维图像，结合图像局部结构信息，设计准则函数，获得双投影矩阵。该方法一定程度上消除了小样本问题，扩大了人脸图像表示的多样性，有利于克服因位移带来的图像不稳定性。对待识人脸图像，由扰动图像设计识别方法，使识别结果更可靠。与传统的人脸识别方法相比，该方法的识别效果更好，Yale和ORL人脸数据库上的实验结果验证了本文方法的有效性。

[1]Turk M，Pentland A.Eigenfaces for recognition[J].Journal of Cognitive Neuroscience，1991，3（1）：71-86.

[2]Belhumeur P N，Hepanha J P，Kriegman D J.Eigenfaces vs fisherfaces：recognition using class specific linear projection[J]. IEEE Trans on Pattern Analysis and Machine Intelligence，1997，19（7）：711-720.

[3]He X，Yan S，Hu Y，et al.Face recognition using laplacianfaces[J].IEEE Trans on Pattern Anal Mach Intell，2005，27 （3）：328-340.

[4]He X F，Yang S C，Han J W，et al.Face recognition using lapalacianfaces[J].IEEE Trans on Pattern Anal and Machine Intell，2005，27（3）：1-13.

[5]Yang J，Zhang D，Frangi A F，et al.Two-dimensional PCA：a new approach to appearance-based face representation and recognition[J].IEEE Trans on Pattern Anal and Machine Intell，2004，26（1）：131-137.

[6]Ye J P.Generalized low rank approximation matrices[J]. Machine Learning Journal，2005，61：167-191.

[7]Ye J P，Janardan R，Li Q.Two-dimensional linear discriminate analysis[C]//Procof Advancesin Neural Information Processing Systems，Vancouver，Canada，2004：1-7.

[8]He X F.Locality preserving projections[D].Chicago：the University of Chicago，2005.

[9]Niu B，Yang Q，Shiu S C K，et al.Two-dimensional Laplacianfaces method forface recognition[J].Pattern Recognition，2008，41：3237-3243.

[10]Guo G，Li S Z，Chan K.Face recognition by support vector machines[C]//Procofthe4th Conferenceon Auto Face and Gesture Recognition，2000：196-201.

[11]Deng C，He X F.Locality sensitive discriminate analysis[C]// Proc of the International Conf on Artificial Intell，Hyderabad，India，2007：708-713.

1.School of Computer Science and Engineering,Nanjing University of Science and Technology,Nanjing 210094,China

2.School of Information Engineering,Yangzhou University,Yangzhou,Jiangsu 225127,China

In order to overcome the instability caused by face detection and curses of dimensionality resulted from small sample size,four new images from one two-dimensional image is generated by horizontal and vertical translation,and a new image database is formed by adding these new images to original image database.Combined with local structure information,this paper designs objective function and obtains dual projection matrix based on two-dimensional images.The proposed method is carried out on disturbing image database.Compared with the traditional face recognition method,it has a better recognition performance,and the experimental results on Yale and ORL face image database show that it is effective and robust.

Two-Dimensional Linear DiscriminateAnalysis（2DLDA）;small sample set problem;disturbing image;feature extraction

A

TP391.4

10.3778/j.issn.1002-8331.1108-0346

ZHANG Guoqing,WANG Zhengqun,WANG Yingjing,et al.Muiti-modal disturbing face recognition algorithm.Computer Engineering and Applications,2013,49（7）：204-207.

国家自然科学基金（No.60875004）；江苏省自然科学基金（No.BK2009184）；江苏省高校自然科学基金（No.10KJB510027）。

张国庆（1986—），男，博士研究生，主要研究方向：机器学习；王正群（1965—），男，博士，教授，主要研究方向：人工智能，机器学习；王颖静（1987—），女，硕士研究生，主要研究方向：机器学习；徐伟（1988—），硕士研究生，主要研究方向：机器学习。

2011-08-24

2011-10-15

1002-8331（2013）07-0204-04

CNKI出版日期：2011-12-09 http://www.cnki.net/kcms/detail/11.2127.TP.20111209.1000.019.html