改进人工蜂群算法在信道分配上的应用

刘俊霞，贾振红，覃锡忠，常 春，王 浩

LIU Junxia1，3,JIA Zhenhong1,QIN Xizhong1,CHANG Chun2,WANG Hao2

1.新疆大学 信息科学与工程学院，乌鲁木齐 830046

2.中国移动新疆分公司，乌鲁木齐 830063

3.新疆机电职业技术学院，乌鲁木齐 830011

改进人工蜂群算法在信道分配上的应用

刘俊霞1，3，贾振红1，覃锡忠1，常 春2，王 浩2

LIU Junxia1，3,JIA Zhenhong1,QIN Xizhong1,CHANG Chun2,WANG Hao2

1.新疆大学 信息科学与工程学院，乌鲁木齐 830046

2.中国移动新疆分公司，乌鲁木齐 830063

3.新疆机电职业技术学院，乌鲁木齐 830011

移动通信网络中频率资源是有限的，为了提高无线资源的利用率，将改进的人工蜂群算法用于解决无线信道分配问题。提出的算法用逐步减小邻域搜索范围的动态步长来均衡局部与全局搜索能力；对单个体引入选择性变异技术，增加了种群的多样性，加快了算法的收敛速度。仿真结果表明，改进后的算法能较好地解决无线信道分配问题，提高了算法的收敛率和收敛速度。

信道分配；人工蜂群算法；选择性变异；搜索步长

1 引言

移动通信系统面临着移动用户数快速增长与有限的频率资源之间的矛盾，为了提高有限的频率资源利用率，采用信道分配技术是行之有效的方法。通常是根据干扰约束条件以及信道分配问题模型，按照不同的算法求解信道的最佳分配方案。在早期，信道分配问题的研究大多是以图形理论或启发式方法为基础的，近年来，主要用神经网络、遗传算法、模拟退火算法和微正则退火算法来处理信道分配问题[1-4]。但在搜索最优解过程中，它们依然存在收敛时间较长，容易陷入或难以摆脱局部最优解等缺点。

为了解决上述缺点，利用固定信道分配的数学模型，在普通人工蜂群算法的基础上，提出了一种用改进的人工蜂群算法来求解最佳信道分配的方案。人工蜂群算法是一类新兴的基于蜜蜂群智能搜索行为的优化算法，它与其他智能算法一样具有优良的优化性能。由于智能算法自身还存在一定缺陷，许多研究者提出了一些改进措施并应用于不同的领域[5-10]。本文针对人工蜂群算法收敛速度慢，易陷入局部最优等缺点，将人工蜂群算法进行改进，并用于解决固定信道分配问题；仿真证明了该算法的优越性。

2 信道分配模型

信道分配问题即频率分配问题，其基本模型是可行性频率分配，目标是在不违反干扰约束的前提下，所有小区都能分配到所需数量的频点。通常只考虑三种主要干扰约束条件：同频干扰（CCC）、邻频干扰（ACC）、共地干扰（CSC）。通常用一个N×N维的兼容矩阵C=Cij(i，j=1，2，…，N)来表示以上主要的干扰约束条件（N为蜂窝系统的小区数），矩阵C中对角元素Cij表示分配给小区i的信道之间的最小间隔，矩阵中的非对角元素Cij(i≠j)表示分配给小区i中的信道与小区 j中的信道的最小间隔。每个小区频率需求数用矩阵R=[ri]，i=1，2，…，N来表示，其中矩阵 R中的元素ri表示第i个小区的频点需求数，可用的频点集合为FN={1 ，2，…，FNum} ，其中FNum=max{fij}，设 fik为给第i个小区的第k个位置分配的频点，fik取值为正整数，fjl同理，它们之间应满足| fik-fjl|≥Cij，(1≤i，j≤N; 1≤k，l≤ri)，目标函数的适应度S(F)定义为信道分配方案F违反约束条件的总数量，Fikjl描述 fik与 fjl是否满足约束条件Cij，数学模型如下[4，11]：

即在给定的C、R和可用频点集合FN，找到使目标函数S(F)值最小即为0的信道分配方案F。

信道分配方案F采用最小间隔实数编码方式，F是一个N×rmax的矩阵，即：

式中rmax是需求向量R的最大值，fij=χ，1≤χ≤FNum，表示将频点 χ分配给第i个小区的第 j个位置，当ri≤j≤rmax时，fij=0。

3 人工蜂群算法

在人工蜂群算法中蜂群主要有引领峰、跟随蜂和侦查蜂，一个蜜源位置(θi)与一个引领蜂(ei)相对应，ei先出去寻找蜜源位置θi,跟随蜂(oi)在舞蹈区等待ei带回蜜源的相关信息，等到ei回到舞蹈区后，oi根据ei的舞蹈得知θi信息，采用公式（4）以概率Pi选择一个θi，并在其邻域内采用公式（5）搜索新蜜源，比较蜜源θi和在其领域内搜索的新蜜源，选择较好的蜜源采蜜。在迭代过程中，若某个oi在设定的搜索次数内没有获得更好的蜜源，ei便放弃该θi，同时成为侦查蜂。并随机搜索新蜜源。

令蜂群数量为M，第t次迭代之后，现有的蜜源位置集合为{θi(t)}，i=1，2，…，M，ei在该次搜索之后，获得的蜜源收益度为H(θi(t))，oi选择θi(t)的概率为：

oi以概率Pi选择θi(t)之后，在其邻域内选择一个新的蜜源(θi(t+1))进行访问，选择的方法为：

其中ψi为随机产生的步长。如果H(θi(t+1))＞H(θi(t))，则用θi(t+1)更蜜源θi(t)，否则θi(t)不变。若在连续的 Limt次迭代之后，均不能发现更优的蜜源，则ei放弃该θi，同时成为侦查蜂随机搜索新蜜源[12-14]。

4 改进的人工蜂群算法

4.1 调整的邻域搜索步长

人工蜂群算法中，跟随蜂在选中的蜜源邻域范围内按式（5）搜索新蜜源，搜索步长具有随机性，算法寻优速度相对较慢，易陷入局部最优或易错过全局最优解。本文根据文献[15]的研究成果，在实验数据的基础上将随机产生的步长改为随迭代次数动态变化的步长，不仅提高了算法的搜索精度，还能较好地平衡局部与全局搜索能力，如式（6）所示：

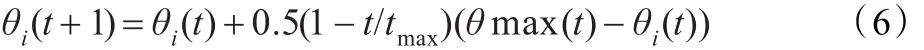
其中，tmax为最大迭代次数；θmax(t)为第t次迭代的最优蜜源位置；0.5(1-t/tmax)是邻域搜索步长的动态权值，它随迭代次数的增加线性减小。该动态权值在算法初期有较大的值，使跟随蜂有较强的全局搜索能力，加快算法收敛速度；在算法后期随迭代次数的增加有较小的值，使跟随蜂有较强的开发能力并增强了算法的搜索精度，从而使蜂群在全局搜索和局部搜索之间达到动态平衡。

4.2 新增的选择性变异技术

为了提高种群的多样性和算法的收敛速度，引入了选择性变异技术。

选择性变异技术是一种单个体进化的方法，在信道分配问题中首先对待变异的个体计算适应度值S(F)，即公式（1）的值。若S(F)＞0，则遍历该个体解F中的每一个频点 fij，用公式（2）进行分析，考察该频点 fij是否对其他小区产生干扰。如果不产生干扰，则什么也不做；如果产生干扰，则需要对该频点 fij进行变异替换。替换频点 fij的频点必须满足第i个小区的共地约束（CSC），即Cii，同时还必须与前PCell个具有较大分配难度的小区满足兼容矩阵所要求的邻频约束（ACC）和同频约束（CCC）。分配难度deg计算公式为[16]：

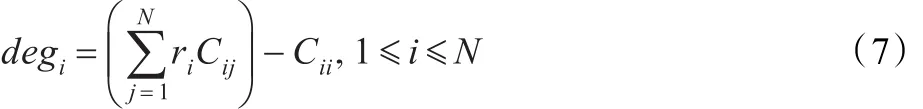
5 信道分配算法及步骤

5.1 蜂群采蜜行为与信道分配问题的对应关系

一个蜜源位置θi与一个信道分配方案Fi相对应，蜜源收益度H(θi)代表该蜜源相对应的信道分配方案Fi的质量，H(θi)越大相应的Fi违反约束条件的频点数越少，即解越接近最优解。具体关系见公式（8）。最大收益度与最佳信道分配方案相对应，搜索最佳蜜源的快慢代表寻找最佳信道分配方案的速度，即算法收敛速度的快慢。

公式（8）中S(Fi)见公式（1）。在信道分配模型中目标是找到最小值，即找到使目标函数S(F)=0的信道分配方案F，该信道分配方案中没有违反干扰约束条件的频点；在改进蜂群算法中目标是求最大值，即蜜源的收益度H(θi)的最大值。信道分配目标函数S(F)的值越小，蜜源收益度值H(θi)越大，当S(F)为最小值等于0时，蜜源收益度 H(θi)达到最大值。因此在改进蜂群算法中，求解最大收益度和信道分配方案中的寻找S(F)=0的最佳信道分配方案是相对应的。

5.2 信道分配算法步骤

步骤1确定蜂群规模M，最大迭代次数tmax，可用频点总数FNum、PCell、Limt的值，引领蜂个数与跟随蜂个数相等，等于M。

步骤2初始化M个可行解Fi(i=1，2，…，M)，计算初始化后的各个可行解的适应度S(F)和各个可行解所对应的蜜源收益度H(θi)，并记录全局最优解θmaxx（收益度H(θi)最大或适应度S(F)最小）。若初始解中有S(F)=0的解，结束算法并输出S(F)=0的信道分配方案，否则执行下一步。

步骤3模拟蜂群行为，oi根据ei的舞蹈得知θi信息，用公式（4）以概率 Pi选择一个θi(t)，并在其邻域内用公式（6）搜索新蜜源θi(t+1)。

步骤4比较蜜源θi(t)和θi(t+1)收益度，选择蜜源收益度大的进行采蜜。

步骤5对步骤4选中的蜜源进行3.2节的选择性变异。计算变异后的蜜源的收益若此次变异产生的蜜源收益度大于变异之前的蜜源收益度，则接受此次变异，否则沿用变异之前选中的蜜源。

步骤6若某些引领蜂对应的蜜源（解）收益度在Limt次循环后都没有改进，则放弃该蜜源，同时引领蜂转变为侦察蜂随机搜索一个新蜜源取代该蜜源。计算本次迭代全局最优解θmax，与上一次迭代的全局最优解比较，选择收益度大的作为本次迭代的全局最优解。

步骤7计算所有蜜源的收益度H(θi)和蜜源相对应可行解的适应度S(F)，若有S(F)=0，即蜜源收益度达到最大值，则结束运算并输出S(F)=0的信道分配方案；否则跳转到步骤3进入下一次迭代。

步骤8若达到最大迭代次数都没有找到使S(F)=0的最佳信道分配方案，则结束运算，并认为算法不收敛。

6 算法仿真

算法用MATLAB 7.0进行仿真，频率分配方案采用实数最小间隔编码方式，种群个数 M=35，引领蜂个数=跟随蜂个数=M,算法循环总代数 tmax=200,Limt=6, PCell=5；对文献[4]的21小区系统进行频率分配，可用频率总数FNum分别取55、65、70、80、90，每种可用频点数各运行50次。图1为本文算法在采用可用频点数为55的收敛代数仿真图，图1中横坐标t为算法迭代次数，纵坐标为适应度函数S(F)的最小值，即信道分配方案F违反约束条件的总数量的最小值。表1为本文算法与文献[4]算法的比较结果；表2为人工蜂群算法与本文算法比较结果。

图1 可用频点数为55的仿真图

表1 本文算法与文献[4]算法仿真结果比较

表2 普通人工蜂群算法与本文算法仿真结果比较

由图1可以看出，在可用频点数不充足为55的情况下，算法也有着较快的收敛速度，仅用17次迭代即可收敛。

从表1的实验结果中看出，当可用频点数设为70时，文献[4]只有90%的收敛率，而本文算法能达到100%的收敛率，且平均收敛代数在3.8代；同时应用到65和55个可用频点数中，文献[4]不收敛，而本文算法的收敛率仍能达到100%，且平均收敛代数也只为5.4代和18代，可用频点为55的仿真结果如图1所示。这表明改进后的人工蜂群算法在频率分配上的效果优于传统的微正则退火算法。从表2的结果中可用看出，在频点数充足且相同的情况下，改进的人工蜂群算法的收敛代数在各可用频点的情况下均小于基本人工蜂群算的收敛代数，并且当频点数为65和55时，基本人工蜂群算法不收敛，而本文算法的收敛率为100%。用本文算法去处理文献[17]的信道分配问题时，仅用1次迭代就可以实现，而文献[17]却用19次迭代才收敛。这些实验结果都证明，改进后的人工蜂群算法在解决信道分配问题上具有优越性和可行性。

7 结束语

本文针对人工蜂群算法邻域搜索步长的随机性、算法的收敛率和收敛速度的问题进行了改进，在信道分配数学模型的基础之上将改进蜂群算法用于解决固定信道分配问题。仿真结果证明：改进人工蜂算法在解决信道分配问题上有较好的寻优能力，在收敛率和收敛速度上优于微正则退火算法和普通人工蜂群算法。

[1]Duque-Anton M，Kunz D，Ruber B，et al.Channel assignment for cellular radio using simulated annealing[J].IEEE Transactions on Vehicular Technology，1993，42（1）：14-21.

[2]罗文坚，曹先彬，王煦法.用一种免疫遗传算法求解频率分配问题[J].电子学报，2003，31（6）：915-917.

[3]朱晓锦，陈艳春，邵勇，等.面向信道分配的分段退火混沌神经网络模型[J].通信学报，2008，29（5）：122-127.

[4]徐俊杰，忻展红.基于微正则退火的频率分配方法[J].南京邮电大学学报，2007，30（2）：67-70.

[5]Karaboga D.An idea based on honey bee swarm for numerical optimization，Technical Report-TR06[R].Kayseri，Turkey：Erciyes University，2005.

[6]Basturk B，Karaboga D.An Artificial Bee Colony（ABC）algorithm fornumericfunction optimization[C]//ProcofIEEE Swarm Intelligence Symposium，2006.

[7]丁海军，冯庆娴.基于boltzmann选择策略的人工蜂群算法[J].计算机工程与应用，2009，45（31）：53-55.

[8]胡中华，赵敏.基于人工蜂群算法的TSP仿真[J].北京理工大学学报，2009，29（11）：978-982.

[9]罗钧，樊鹏程.基于遗传交叉因子的改进蜂群优化算法[J].计算机应用研究，2009，26（10）：3716-3717.

[10]Mezura-Montes E，Velez-Koeppel R E.Elitist artificial bee colony forconstrained real-parameteroptimization[C]//Proc of IEEE Evolutionary Computation（CEC），Barcelona，2010：1-8.

[11]Aardal K I，Hoesel S P M V，Koster A M C A，et al.Models and solution for frequency assignment problems[M].Berlin：Springe-Verlag，2001.

[12]Karaboga D，Basturk B.On the performance of Artificial Bee Colony（ABC）algorithm[J].Applied Soft Computing，2008，8：687-697.

[13]Karaboga N.A new design method based on artificial bee colony algorithm fordigitalIIR filters[J].Journalofthe Franklin Institute，2009，346（4）：328-348.

[14]李端明，程八一.基于人工蜂群算法求解不同尺寸工件单机批调度问题[J].四川大学学报：自然科学版，2009，46（3）：657-662.

[15]池元成，朱浩，方杰，等.改进粒子群优化算法在亚轨道飞行器固液混合发动机设计中的应用[J].航空动力学报，2011，26 （9）：1-6.

[16]Seyed A G S，Hamidreza A.A hybrid method for channel assignment problems in cellular radio networks[C]//Proceeding of IEEE WCNC，USA，2006.

[17]池越，赵东明，夏克文，等.基于QPSO算法的信道分配方法[J].通信技术，2009，42（2）：204-209.

1.Institute of Information Science and Engineering,Xinjiang University,Urumqi 830046,China

2.Xinjiang Mobile Communication Company,Urumqi 830063,China

3.Xinjiang Institute of Electrical and Mechanical Technology,Urumqi 830011,China

The frequency resources of mobile communication network are limited,in order to improve wireless resource utilization,the improved artificial bee colony algorithm is to solve the wireless channel allocation problem.The proposed algorithm with gradually reduced dynamic step balances local and global search capability.The introduction of the single-individual selective mutation increases population diversity and the convergence speed.Simulation results show that the improved algorithm can be better to solve the wireless channel allocation,improve the convergence rate and convergence speed of algorithm.

channel assignment;artificial bee algorithm;selective mutation;search step

A

TN91

10.3778/j.issn.1002-8331.1108-0257

LIU Junxia,JIA Zhenhong,QIN Xizhong,et al.Applications in channel assignment based on improved artificial bee colony algorithm.Computer Engineering and Applications,2013,49（7）：119-122.

中国移动新疆分公司研究发展基金（No.xjm2010-1）。

刘俊霞（1980—），女，讲师，主要研究方向：信号与信息处理；贾振红，男，教授，博士生导师，研究方向：信号与信息处理；覃锡忠，副教授；常春，高级工程师；王浩，高级工程师。E-mail：ljxljx@sina.cn

2011-08-31

2011-11-22

1002-8331（2013）07-0119-04

CNKI出版日期：2011-12-09 http://www.cnki.net/kcms/detail/11.2127.TP.20111209.1001.032.html