基于启发式信息的非凸放疗规划模型的求解方法
2013-08-04淮北师范大学计算机科学与技术学院安徽淮北235000
1.淮北师范大学 计算机科学与技术学院,安徽 淮北 235000
2.南阳师范学院 计算机与信息技术学院,河南 南阳 473061
3.连云港市第二人民医院 医学影像科,江苏 连云港 222005
1.淮北师范大学 计算机科学与技术学院,安徽 淮北 235000
2.南阳师范学院 计算机与信息技术学院,河南 南阳 473061
3.连云港市第二人民医院 医学影像科,江苏 连云港 222005
1 引言
调强放射治疗是目前对恶性肿瘤进行治疗的有效手段之一,这种治疗手段通过可调的照射角度、可调的各照射野射线强度,在待治疗区域上形成可调的放射线剂量分布,保证肿瘤杀灭区域的剂量达到治疗水平,而非肿瘤区域的放射剂量控制在发生并发症的水平以下,危险区域的放射剂量则控制在最低水平。这样强度可调的三维形状适应性很强的放疗手段改变了过去传统放疗并发症较高的弊端,已经在欧美等发达国家对头颈部癌、前列腺癌、肺癌、脑癌等癌症的治疗中广泛使用,目前国内的一些大中城市的医院也在推广普及这种治疗技术。
调强放疗医疗器械的生产厂商主要还是国外的知名公司,如通用、瓦里安等。该类器械的一个关键技术就是如何从医生设定计划逆向求解得到放疗规划结果,即前期通过医生对待治疗区域器官、照射靶区的勾勒后,形成剂量要求和剂量约束条件,送入放疗逆向求解系统中进行优化求解,最终得到硬件设备可以施行的照射方案。其中逆向优化过程的一个关键环节就是得到各照射野的照射分布图[1-3]。一个好的照射分布图应该具备以下两个方面的要求。(1)待照射靶区的剂量接收值应与医生设定的计划剂量值尽可能相等,且保证剂量分布的一致性。(2)待照射靶区周边组织的剂量接收值应越低越好,从而在靶区三维轮廓上形成剂量快速下降的分布趋势,特别是一些危险的串行组织需要严格限制剂量上限,而一些并行组织则可以对剂量约束适当放松。
目前已经有大量的文献正关注于物理剂量模型的建立和相应的求解算法[4-5],考虑到求解算法的高效性要求,目前的逆向计划大多转化为线性或二次规划模型[6-8]。在这些模型中,剂量逼近程度一般采用实际剂量与设定剂量的绝对差值或绝对差值的平方进行描述;并广泛采用剂量体积曲线的多点限制模式,即通过剂量体积图曲线的调节指导放疗优化,让正常组织满足一定的剂量体积比要求的情况下,尽可能地让待治疗区域达到放射剂量要求。
非常可惜的是,带有剂量体积限制的数学规划模型为非凸规划问题[9-11],为了求解这样一类较难的数学问题,近几年来国内外科学家提出了许多求解方法,取得了一定的成效,但离获得最优解仍有较大距离。
Cotrutz等[12]使用基于体素权重系数的方法来帮助求解,在他们的方法中,首先对线性规划问题或二次规划问题进行初始求解,并获得初始剂量分布,然后按该剂量分布,根据低剂量体素更加容易抑制为更低剂量、高剂量体素更加容易给予更高剂量这样的启发式信息为指导,重新对体素的权重进行分配,再次进行优化;重复上述过程直到达到优化限定条件。这样的启发式信息有一定的直观依据,但是形而上的想法缺乏科学依据。本文提出一种新的更加科学的启发式方法对上述非凸规划问题进行求解,并在四个病例上进行了相关实验。实验结果证实,新的启发式方法能够获得更优的逆向计划。
2 方法
2.1 强度照射分布图优化问题
整个待治疗区域的人体组织被分为两个部分,且用体素进行离散化,一部分为待照射靶区T={T1,T2,…,Tu},相应的体素数目为…,STu,另一部分为正常组织和危险器官组织N={N1,N2,…,Nv},相应的体素数目为…,。照射分布图用像素进行离散化,按照照射野的顺序以及分布图逐行的顺序,用列向量X进行描述,FT=为靶区剂量作用矩阵,为正常组织和危险器官组织的剂量作用矩阵。任意一个元素 fi,j表示第j个像素采用单位强度照射时对第i个体素所产生的剂量沉积值。 DT=FT·X和 DN=FN·X代表整个待照射区域在强度分布图X下的三维剂量分布。设定医生指定的剂量为,…,,正常组织以及危险区域组织的剂量上限为,…,
给出物理剂量模型所广泛采用的线性约束二次规划模型如下:
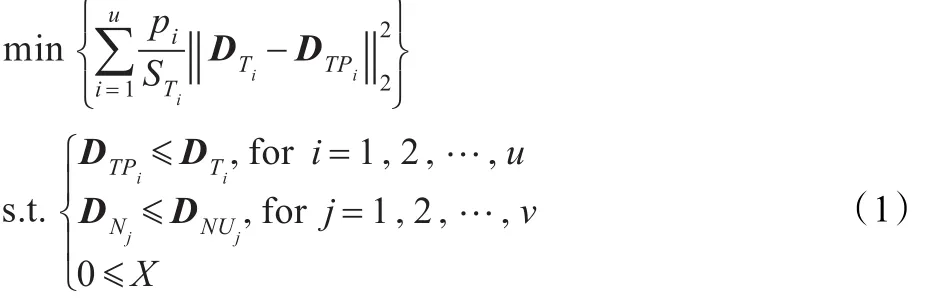

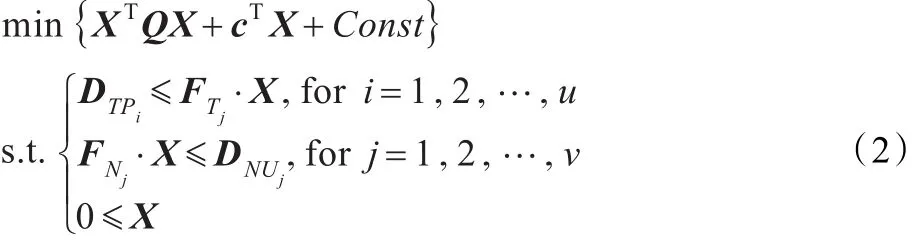
2.2 剂量体积曲线限制条件
放射科临床医生常用的一个概念为剂量体积曲线,这个曲线能够从宏观上描述某个器官的剂量分布生物学特征。剂量体积曲线的横轴为剂量值,纵轴为体积百分比,曲线上的每一个点表示某个器官中低于某个剂量的组织体积占整个器官组织体积的百分比。因此该曲线为一条递减曲线。

而相应的剂量体积曲线限制即要求曲线在某个点的上方或某个点的下方。以正常组织为例,剂量体积曲线限制条件一般限定曲线在一个点或几个点的下方。一般描述为某个器官组织接受ϑ Gy剂量或更高剂量的体素数目不超过该器官组织总体素数目的η%,其中“Gy”为放射剂量单位。直观上,即要求曲线在点( ) ϑ,η的下方。

图1 剂量体积曲线及约束点
设正常组织和危险器官组织 N1,N2,…,Nv有剂量体积限定条件 DVC1,DVC2,…,DVCv,其中为剂量体积限定条件 DVCi中的约束点个数,为相应的约束点。由此形成以下的带有剂量体积约束的数学规划问题:
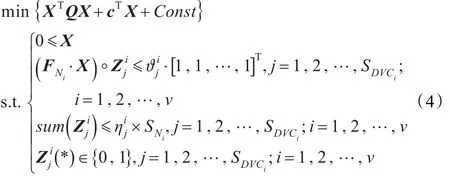
对于临床医生常用的一个概念被引入到逆向计划中却带来了求解过程的极大困难,因为上述模型为组合优化模型。
2.3 正规化空间内的空间距离启发信息
上述组合优化模型的求解为非凸规划问题的求解,获得该问题的最优解是NP难问题。目前国外一些参考文献的求解方法是采用基于体素权重系数的问题转换求解思路,即通过对各体素设定一定的权重,从而将上述问题转换为凸规划问题进行求解,当然,还有一些思路则回避剂量体积曲线约束,考虑采用其他约束取代这类非凸约束,从而转换为凸规划问题。对于后者,认为约束条件的转换已经基本违背了临床医生的剂量设定初衷,因此本文不予考虑。对于问题转换思路,本文予以采纳,即将上述问题转换为凸规划从而获得转换问题的最优解,但是对于体素排序的思路,本文提出新的启发式想法,即从原来的剂量高低排序方式转换为二次规划正规化空间内的空间距离远近排序方式。具体算法流程如图2所示。

图2 优化算法流程图

根据Cholesky分解,Q=RTR,带入 x=R-1y,上述模型转换为:

对于线性约束二次规划问题:
设(R-1)Tc=e,BR-1=G,上述线性约束二次规划问题有以下的正规化形式:

下面通过一个简单的示例来对剂量高低排序方式以及二次规划正规化空间内的空间距离远近排序方式进行比较。
该示例只有一个规划靶区,并为一个凹的形状,另一个危险组织区域为圆形,并一定程度地被规划靶区包围。照射方向为五个均匀分布的方向,靶区设定的剂量为单位剂量,危险组织区域的最大剂量不能超过0.5,正常组织剂量不超过0.8,危险组织区域的剂量体积曲线要求接受高于0.3剂量的体积大小不超过50%(如图3所示)。

图3 示例初始剂量分布示意图
求解了不带有剂量体积曲线限制条件的规划问题,并按照剂量高低排序方式以及二次规划正规化空间内的空间距离远近排序方式对危险组织区域进行了排序,排序结果如图4所示,显然,基于二次规划正规化空间内的空间距离远近排序方式的排序结果更加自然,远离靶区的体素具有更高的优先级被纳入线性约束中去,从而达到所要求的剂量体积曲线约束。

图4 危险组织区域的正规化空间内空间距离和剂量排序比较示意图
2.4 实验设定
为了验证所提方法的有效性,使用四个临床实验数据进行了测试,剂量设定值见表1~4。本文中实验强度矩阵的计算基于QIB剂量计算引擎。所有实验均在Matlab计算平台下进行。
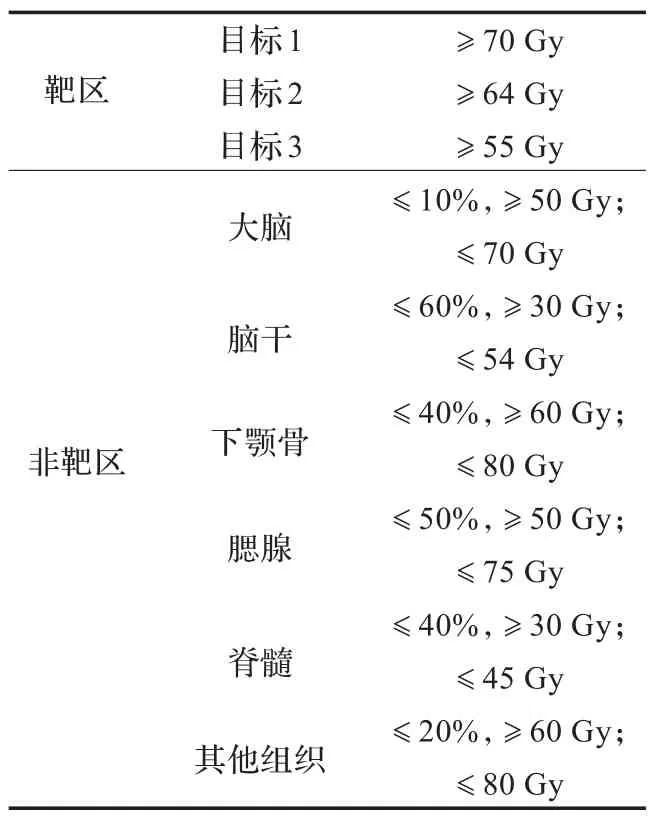
表1 头颈部测试例的剂量设定值

表2 前列腺测试例的剂量设定值

表3 肺部测试例的剂量设定值
3 实验结果和分析

表4 口咽部测试例的剂量设定值
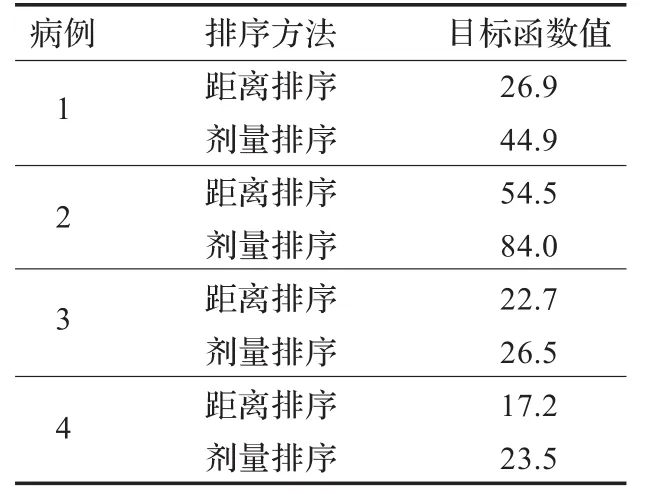
表5 优化结果比较

图5 头颈部测试例的剂量体积曲线
在四个测试病例上,对基于剂量高低排序方式的启发信息以及基于正规化空间内的空间距离远近排序方式的启发信息进行了实验对比,表5中给出了两种方法所得到的目标函数值。图5~8中给出了两种方法得到的靶区各照射目标以及非靶区各器官的剂量体积曲线比较结果(标有实心图例的实线是本文方法的结果,标有对应的虚心图例的虚线是基于剂量高低排序方式方法的结果)。图9~12中还给出了两种方法得到的断层剂量分布图的比较结果。实验结果显示,在达到同样的剂量体积曲线限制条件的约束情况下,采用提出的启发信息,病例一的目标函数值降低了((26.9-44.9)/44.9=-40%,病例二降低了(54.5- 84.0)/84.0=-35%,病例四降低了(17.2-23.5)/23.5=-27%),除病例三以外降低幅度均较大。通过比较靶区各目标的剂量体积曲线,可以看到实线比虚线下降得更为陡峭,也就是说采用本文提出的启发信息,靶区的剂量分布更加均匀,且更接近于所设定的处方剂量值,通过断层剂量分布图可以明显地得到这个结论。
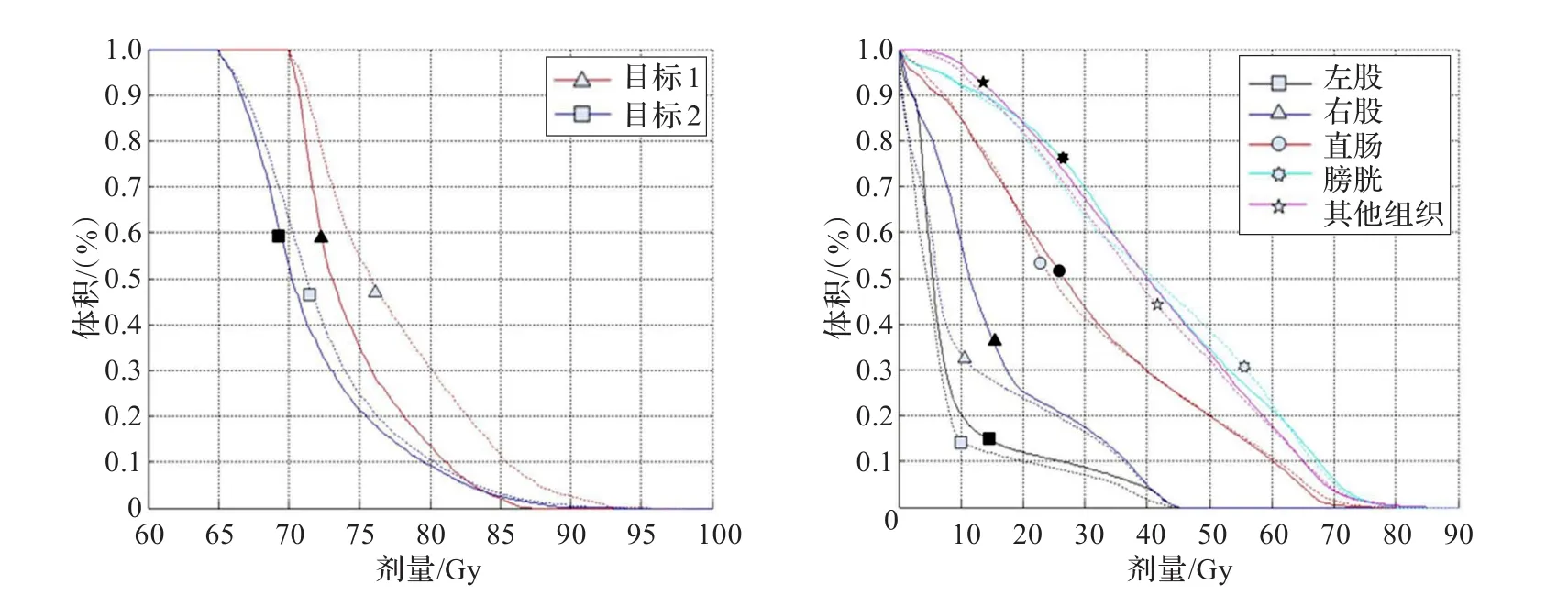
图6 前列腺测试例的剂量体积曲线

图7 肺部测试例的剂量体积曲线

图8 口咽部测试例的剂量体积曲线

图9 头颈部测试例的某断层剂量分布图

图10 前列腺测试例的某断层剂量分布图

图11 肺部测试例的某断层剂量分布图

图12 口咽部测试例的某断层剂量分布图
4 结束语
本文对调强放疗数学规划问题中的非凸规划提出一种新的启发式思想,利用这种思想得到的非凸规划问题求解方法能够获得更优的优化结果。在四个病例上的实验结果证实了所提新方法的有效性。此外,这种启发思想能够在其他非凸数学规划问题的求解中同样得到广泛应用。
[1]Bortfeld T.IMRT:a review and preview[J].Physics in Medicine and Biology,2006,51:363-379.
[2]Hatano K,Araki H,Sakai M,et al.Current status of Intensity-ModulatedRadiation Therapy(IMRT)[J].International Journal of Clinical Oncology,2007,12:408-415.
[3]Yu C X,Amies C J,Svatos M.Planning and delivery of intensity-modulated radiation therapy[J].Medical Physics,2008,25:5233-5241.
[4]Shepard D M,Ferris M C,Olivera G H,et al.Optimizing the delivery of radiation therapy to cancer patients[J].Siam Review,1999,41:721-744.
[5]Lim J,Ferris M C,Wright S J,et al.An optimization framework for conformal radiation treatment planning[J].INFORMS Journal on Computing,2007,19:366-380.
[6]Morrill S M,Lane R G,Wong J A,et al.Dose-volume considerations with linear programming optimization[J].Medical Physics,1991,18:1201-1210.
[7]Breedveld S,Storchi P R M,Keijzer M,et al.Fast,multiple optimizations of quadratic dose objective functions in IMRT[J]. Physics in Medicine and Biology,2006,51:3569-3579.
[8]Censor Y,Ben-Israel A,Xiao Y,et al.On linear infeasibility arising in intensity-modulated radiation therapy inverse planning[J].LinearAlgebra and ItsApplications,2008,428:1406-1420.
[9]Deasy J O.Multiple local minima in radiotherapy optimization problems with dose-volume constraints[J].Medical Physics,1997,24:1157-1161.
[10]Wu Q,Mohan R.Multiple local minima in IMRT optimization based on dose-volume criteria[J].MedicalPhysics,2002,29:1514-1527.
[11]Wu C,Jeraj R,Mackie T R.The method of intercepts in parameter space for the analysis of local minima caused by dose-volume constraints[J].Physics in Medicine and Biology,2003,48:149-157.
[12]Cotrutz C,Xing L.Using voxel-dependent importance factors for interactive DVH-based dose optimization[J].Physics in Medicine and Biology,2002,47:1659-1669.
基于启发式信息的非凸放疗规划模型的求解方法
张栋冰1,兰义华2,万金鑫3
ZHANG Dongbing1,LAN Yihua2,WAN Jinxin3
1.School of Computer Science and Technology,Huaibei Normal University,Huaibei,Anhui 235000,China
2.School of Computer and Information Technology,Nanyang Normal University,Nanyang,Henan 473061,China
3.Medical Imaging Department,Lianyungang Second People’s Hospital,Lianyungang,Jiangsu 222005,China
For the inverse planning process of intensity-modulated radiotherapy—the non-convex mathematical programming for the fluence map optimization with dose volume constraints,this paper presents a novel and scientific heuristic information—distance priority value in normalized space.Compared to the traditional dose ordering heuristic information,this new method leads to better solutions.A phantom example and four test cases show the effectiveness of the proposed method.
non-convex fractional programming;heuristic algorithm;intensity-modulated radiation therapy technology;linear constrained quadratic programming
针对调强放疗逆向优化过程中的关键环节——各照射野的强度照射分布图在带有剂量体积曲线限制条件下的非凸数学规划问题,提出了一种新颖的更加科学的启发式信息——正规化空间内的空间距离排序值。与传统的剂量排序启发式信息相比较,新方法可以得到更好的解。一个简单示例和四个测试病例表明了该方法的有效性。
非凸数学规划;启发式求解;调强放疗;线性约束二次规划
A
TP391
10.3778/j.issn.1002-8331.1302-0021
ZHANG Dongbing,LAN Yihua,WAN Jinxin.Method based on heuristic information for solving non-convex model of radiotherapy planning.Computer Engineering and Applications,2013,49(11):265-270.
国家自然科学基金(No.61102117)。
张栋冰(1974—),男,讲师,研究领域为图像处理、算法优化;兰义华,男,博士,讲师,研究领域:图像处理、算法优化;万金鑫,男,研究员级高级工程师,研究方向:医学图像诊断方法。E-mail:291508366@qq.com
2013-02-04
2013-04-15
1002-8331(2013)11-0265-06
