融合粗糙集和灰色GM(1,N)的西安市供水量预测
2013-08-04西安理工大学理学院应用数学系西安710054
西安理工大学 理学院 应用数学系,西安 710054
西安理工大学 理学院 应用数学系,西安 710054
1 引言
西安市是关中地区政治、经济、文化发展的核心,虽然有着八水绕长安之美誉,但是随着社会的高速发展,水资源紧缺已成为制约西安市可持续发展的瓶颈。由于用水量是一个复杂的、相互关联的体系,受到政策,人口,气象等因素影响呈非线性的波动状态,如何有效地预测出未来用水量,将会对市政决策者在水资源规划和管理方面提供科学依据。
目前,对于用水量预测已经取得了一定的研究成果,主要包括:时间序列预测法[1],马尔科夫预测法[2],主成分分析法[3],灰色系统理论预测法[4],但是随着计算机技术的发展,小波分析,支持向量机,神经网络,粒子群优化算法,计算机仿真算法等一批智能算法的出现,为复杂的预测问题提供了更加有利的科学工具,许多学者将传统预测法与智能算法相结合,如基于最小二乘支持向量机的供水量预测模型[5],粒子群算法和神经网络结合的预测法[6],基于时间序列和神经网络理论的SIMULINK仿真模型[7]等均取得了较好的效果,它们在一定程度上提高了预测的精度。
本文在深入分析各种方法优缺点的基础上,发现在选择影响供水量的主要因素时,大部分学者采用主成分分析法或者支持向量机算法,而鲜见采用粗糙集属性约简算法,于是尝试着用粗糙集中知识的依赖度理论对多属性进行约简,在约简基础上建立灰色GM(1,N)预测模型,对西安市年供水量进行预测。
2 基本理论与方法
2.1 粗糙集知识的依赖度理论
粗糙集理论[8]具有很强的定性分析能力,能够有效地表达不确定的或不精确的知识,善于从数据中获得知识,并能利用不确定、不完整的经验知识进行推理等,因此在知识获取、机器学习、规则生成、决策分析、智能控制等领域获得广泛运用。粗糙集理论中对象的隶属函数值却依赖于知识库,它可以从所需处理的数据中直接得到,无需外界的任何信息,所以用它来反映知识的模糊性是比较客观的。
定义1(集合的下近似和上近似)给定知识库K= (U,S),其中,U为论域,S表示论域U上的等价关系族,则∀X⊆U和论域U上的一个等价关系R∈IND(K),(IND(K)表示知识库K=(U,S)中所有等价关系),定义子集 X关于知识R的下近似和上近似分别为:
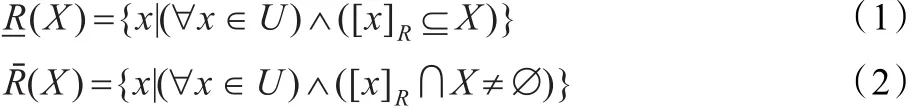
集合 posR(X)=称为 X的R正域。
定义2(知识的依赖度)给定一个决策表DT=(U,C∪D,V,f),C为条件属性,D为决策属性,V是信息函数 f的值域。
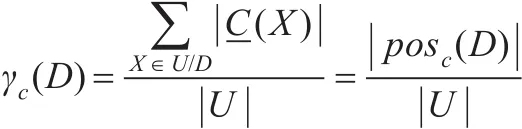
表示决策属性依赖于条件属性的程度。其中|•|为集合的基数。
2.2 灰色GM(1,N)模型
定义3(灰色关联度)设系统行为序列
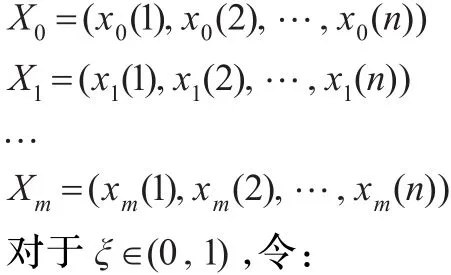
γ(x0(k), xi(k))=
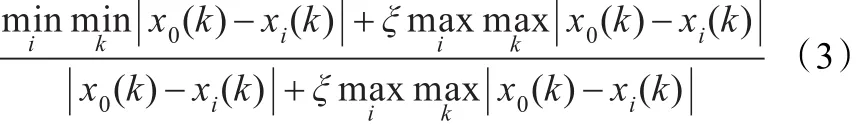

定义4(GM(1,N)模型)[9]设
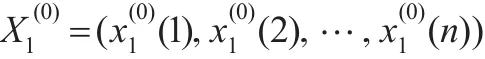
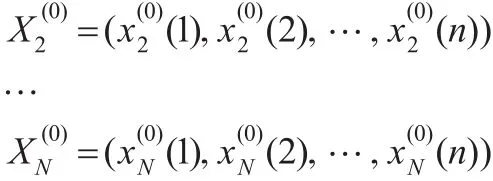
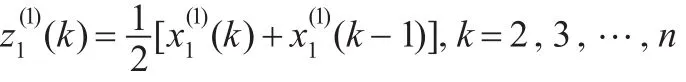
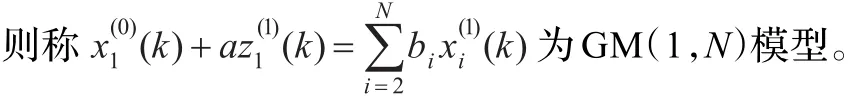
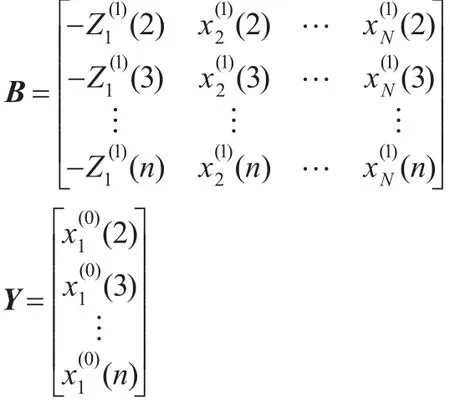
2.3 预测步骤
有以上理论支持,可以得到融合粗糙集和灰色理论预测方法的预测步骤如下:
(1)采集相关原始数据。
(2)对于原始数据无量纲化处理。
(3)运用等距离离散化算法处理(2)所得数据。
(4)根据粗糙集的知识依赖度理论计算出依赖度较大的条件属性。
(5)建立GM(1,N)预测模型。
3 实例分析
本文以西安市2001-2009年全年供水总量(用D表示)为系统特征因素,初步选取对全年供水量有影响的八个因素:西安市生产总值(用a表示)、居民家庭用水量(用b表示)、社会固定资产投资(用c表示)、人口(用d表示)、生产用水(用e表示)、日综合生产能力(用f表示)、人均日生活用水量(用j表示)、年降水量(用k表示)作为研究对象(数据来源于2002-2010年《陕西省统计年鉴》,见表1)。其中2001-2007年数据用于建模,2008-2009年数据用于模型检验,然后对2010年和2011年的全年供水总量进行预测。
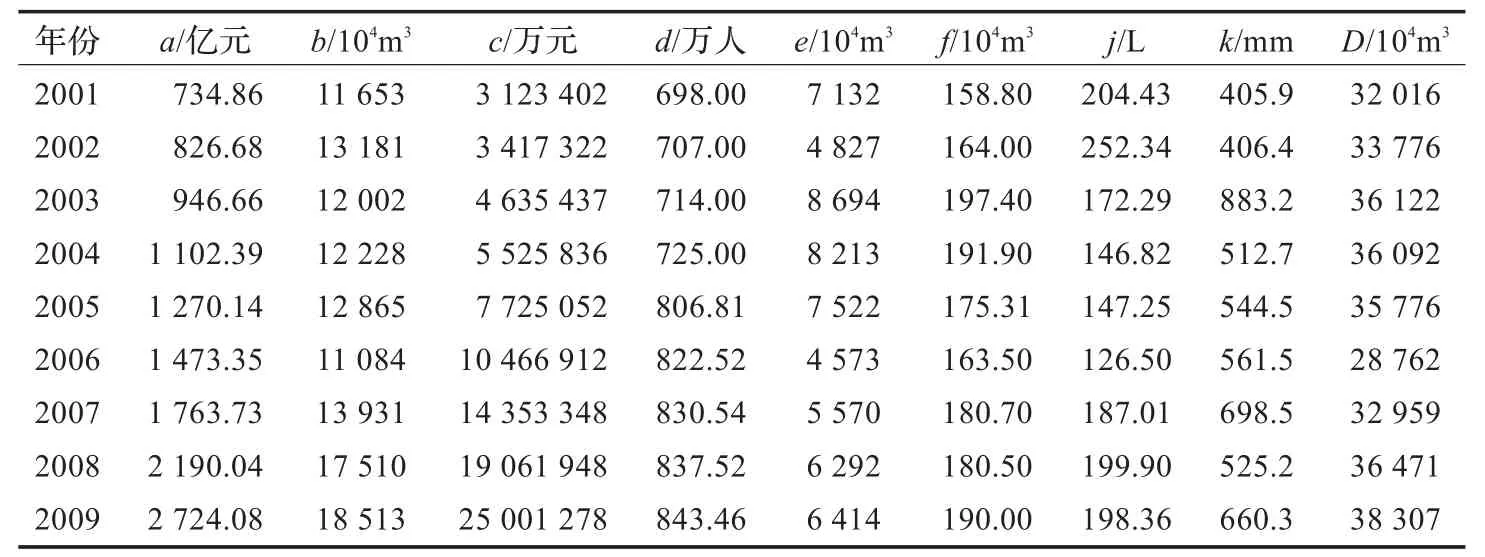
表1 全年供水量与相关因子原始数据1)
3.1 无量纲化处理
3.2 决策表的离散化处理
将无量纲化处理过的数据离散化,这里采用等距离离散化算法[10],该算法基本思想:将连续属性取值区间分成N个小区间(N是决策者取定的),某属性的取值范围[a,b],则N个区间取值为:

本算例中,对2001-2009年的数据进行离散化,可得离散化后的决策表2。
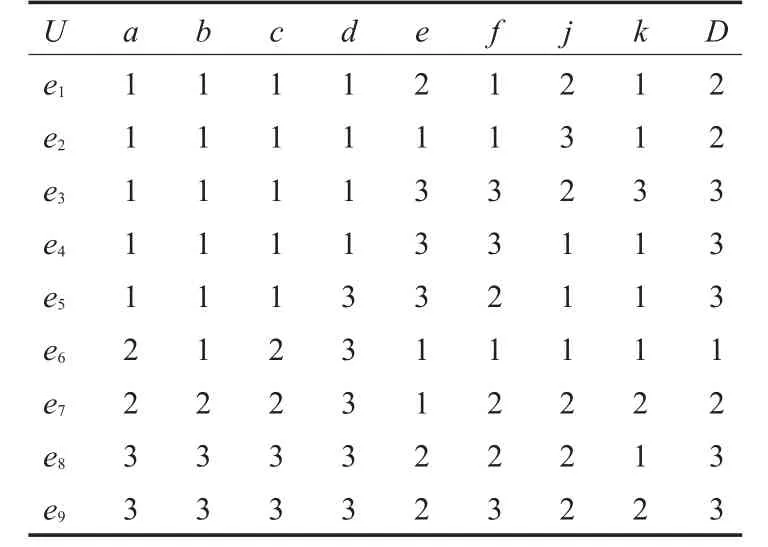
表2 离散化后的样本信息决策表
3.3 基于粗糙集知识依赖度理论的供水量预测因子筛选
在表2中,将每一年的行数据看成一个集合,则论域U={e1,e2,…,e9},将每一个指标看成一个属性,则属性集合 C={a,b,c,d,e,f,j,k,D},其中 D 为决策属性,可以得到条件属性对决策属性的分类如下:
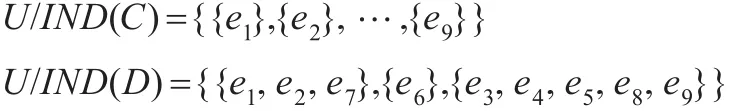
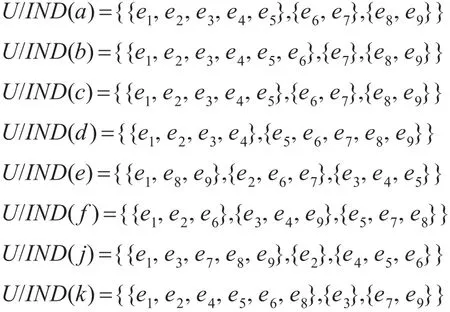
决策属性关于各个条件属性的正域分别为:
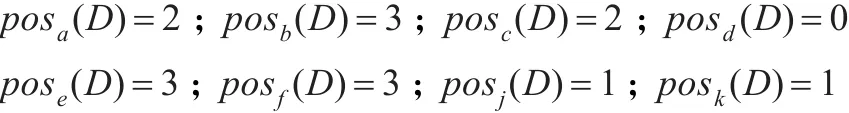
再根据定义2,可以计算出决策属性对每个条件属性的依赖度如下:
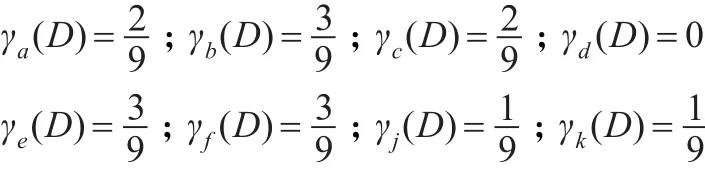
故排序结果为b=e=f≻a=c≻j=k≻d。
3.4 基于灰色关联度理论的供水量预测因子筛选
根据公式(3)计算得到各个条件属性的灰关联度。见表3。故排序结果为 f≻d≻b≻e≻j≻k≻a≻c。
3.5 建立GM(1,N)模型

表3 各条件属性的灰关联度
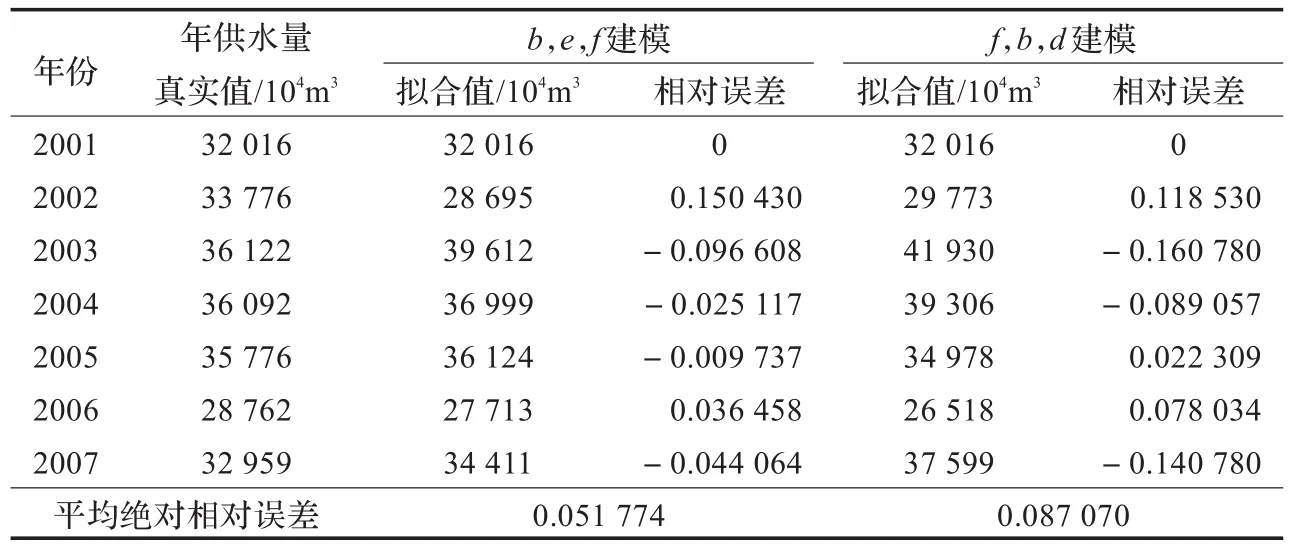
表4 两种方法选取的因子建模结果比较
知识依赖度越高说明该条件属性对决策属性影响越大,灰色关联度越高的相关因素序列对系统特征行为序列影响也越大。这里对粗糙集知识依赖度所选取的因子b,e,f和灰色关联度所选取的因子f,d,b分别建立GM(1,4)模型,并进行比较,所得结果见表4。
由表4对比结果可知,选取b,e,f建立的GM(1,4)模型的拟合精度比f,b,d建立的模型拟合精度高,所以选取b,e,f建立的 GM(1,4)模型作为预测模型,并用 2008年和2009年数据进行模型检验,并与离散GM(1,1)模型的预测值进行比较,所得结果见表5。
通过表5对比结果,选取b,e,f建立的GM(1,4)模型其相对误差最小。由于相关因素越多,对其预测误差将会代入GM(1,4)模型,从而增加了预测误差,所以用此模型做短期预测比较合适。根据实际情况采取线性回归法,三次指数平滑法,最小二乘法,GM(1,1)等方法预测出居民家庭用水量(b)、生产用水量(e)、日综合生产能力(f)。这里采用GM(1,1)模型分别预测出2010年和2011年的相关因素序列值如表6所示。

表5 模型检验
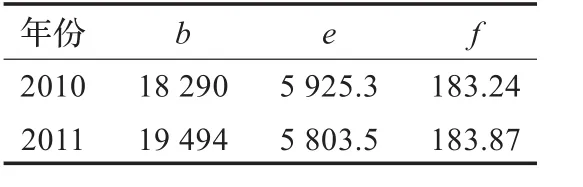
表6 相关因素预测值104m3
选择由b,e,f建立的GM(1,4)模型作为预测模型,其参数列如下:
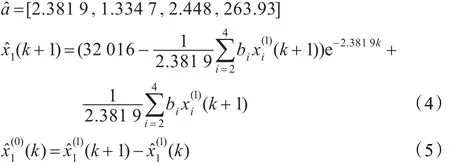
其中式(4)是GM(1,4)模型的时间响应式,式(5)是累减还原式。
由式(4)和(5)可得2010年和2011年西安市年供水量分别为:33 659×104m3和37 271×104m3。
4 结束语
本文用粗糙集知识依赖度理论找出了对供水量有较大影响的三个因素:居民家庭用水量、生产用水量、日综合生产能力建立GM(1,4)模型。通过实例验证可以看出本文所提方法建立的模型确实是可行的。对未来两年所作的预测值也符合西安市十二五规划要求。但是也有一些需要改进的地方,用GM(1,N)模型进行预测,需要对相关因素进行评估和预测,会将相关因素预测误差代入GM(1,N)模型,对预测结果产生不良影响。GM(1,N)模型用于短期预测效果好于长期预测。
[1]张可义.非平稳时间序列建模与预报在供水管网水量预测中的应用研究[D].北京:北京科学研究总院北京机械工业自动化研究所,2007.
[2]李小冰,蔡焕杰,张鑫,等.秃尾河流域降水量权马尔科夫链模型预测研究[J].干旱地区农业研究,2009,27(6):252-256.
[3]刘思峰,党耀国,方志耕,等.灰色系统理论及其应用[M].5版.北京:科学出版社,2010.
[4]Chen X H.Uncertainty research in rough set data analyzing[D]. Beijing:Tsinghua University,2000:69-70.
[5]吕王勇,赵凌,陈东.基于主成分分析的四川省用水量预测[J].水资源与水工程学报,2009,20(6):84-87.
[6]赵宇哲,武春友.灰色震荡序列GM(1,1)模型及在城市用水中的应用[J].运筹与管理,2010,19(5):156-166.
[7]Xie Ying,Zheng Hua.Water supply forecasting based on developed LS-SVM[C]//3rd IEEE Conference,Singapore,2008:2228-2233.
[8]王亮,张宏伟,岳琳,等.PSO-BP模型在城市用水量短期预测中的应用[J].系统工程理论与实践,2007,27(9):165-170.
[9]雷鸣,张宏伟,闫静静.城市用水量预测的SIMULINK仿真技术研究[J].中国给水排水,2010,26(15):54-57.
[10]苗夺谦,李道国.粗糙集理论、算法与应用[M].北京:清华大学出版社,2008.
融合粗糙集和灰色GM(1,N)的西安市供水量预测
孙 强,王秋萍
SUN Qiang,WANG Qiuping
Department of Applied Mathematics,School of Sciences,Xi’an University of Technology,Xi’an 710054,China
For multivariate prediction problems,this paper constructs fusion prediction model of rough set and grey system theory. The model adopts theory of knowledge dependency to reduce multiple attributes,GM(1,N)model is established based on knowledge reduction.Annual water supply quantity of Xi’an is fitted and forecasted by using the established model,and fitted values is compared with values of DGM(1,1)model.The experimental results indicate that this method has advantage over selecting the factors of influence by traditional grey incidence grade.Thereby,a kind of method suitable for water supply forecasts is provided.
rough set;knowledge dependency;grey correlation;GM(1,N)model
对于多变量预测问题,构造了粗糙集和灰色理论的融合预测模型。该模型运用粗糙集的知识依赖度理论对多属性进行约简,在约简基础上建立GM(1,N)模型。用所建模型对西安市年供水量进行了拟合和预测,并与离散灰色GM(1,1)模型作比较。实验结果表明该模型的预测精度高于传统的用灰关联度选择影响因子建模,从而为供水量预测问题提供了一种新方法。
粗糙集;知识的依赖度;灰色关联度;GM(1,N)模型
A
O29;C931
10.3778/j.issn.1002-8331.1110-0169
SUN Qiang,WANG Qiuping.Water supply quantity forecast of Xi’an via combination rough sets with GM(1,N)model. Computer Engineering and Applications,2013,49(11):237-240.
“十一五”国家科技支撑计划项目子课题(No.2008BAE63B03)。
孙强(1983—),男,硕士生,研究方向:灰色预测及其粗糙集应用研究;王秋萍(1964—),女,博士,副教授,主要研究领域:预测与决策分析理论、方法及应用,系统工程。E-mail:sunqiang1022@163.com
2011-10-11
2011-12-02
1002-8331(2013)11-0237-04
CNKI出版日期:2012-03-08 http://www.cnki.net/kcms/detail/11.2127.TP.20120308.1520.035.html
