基于集合枚举树的最小属性约简算法

成都信息工程学院 软件工程学院，成都 610225

JIANG Yu

成都信息工程学院 软件工程学院，成都 610225

College of Software Engineering,Chengdu University of Information Technology,Chengdu 610225,China

粗糙集理论是由波兰学者Pawlak于1982年提出的[1-2]，是一种刻划具有不完整性和不确定性信息的全新数学工具。其主要思想是在保证知识库的分类能力不变的前提下，通过知识约简导出问题的决策或分类规则。知识约简问题是粗糙集理论的一个核心问题[3-4]。所谓知识约简，就是在保证知识库分类能力不变的条件下删除其中不相关或不重要的冗余知识。

一般来讲，一个决策表的属性约简不是唯一的，通常人们往往希望能够找到一个冗余度最小的属性约简，该属性约简被称为最小属性约简。对任一给定决策表，若属性约简算法能确保找到其最小属性约简，则该算法称为最小属性约简完备算法。然而，S.K.M Wong和W.Ziarko已经证明了找一个决策表的最小约简是NP-hard问题[3]。导致NP-hard问题的主要原因是属性的组合爆炸问题。目前已存在一些属性约简算法能够找到决策表的最小属性约简[4-12]，但它们要么不是完备的最小属性约简算法，要么通过穷举求出问题的所有约简或所有最小约简。

本文重新定义了属性重要度，给出了条件属性集上的序关系，基于该序关系构建集合枚举树，提出了一种基于集合枚举树的最小属性约简算法。该算法采用至顶向下、层优先搜索策略遍历集合枚举树从而找到最小属性约简。为了减少搜索空间，提高算法效率，该算法采用了两种剪枝策略剪去集合枚举树中冗余节点。一种剪枝方法是父集剪枝，如果一个集合的父集不是属性约简，则该集合一定也不是属性约简，该策略是通过提前停止集合枚举树的构造而对树剪枝。另一种剪枝方法是属性核剪枝，因为所有的属性约简都包含核属性，从而可以剪去集合枚举树中不含核属性的节点。最后，优化计算确保同一集合的正域只求解一次。

1 粗糙集的相关概念

对于决策表 S=(U，C，D，V，f)，U 是论域，C是条件属性的集合，D是决策属性集合，V是属性值的集合，f:U× (C∪D)→V是信息函数，U、C、D和V都是非空有限集且C ∩ D=。表1为某一决策表，且C={a，b，c，d}，D={e}。

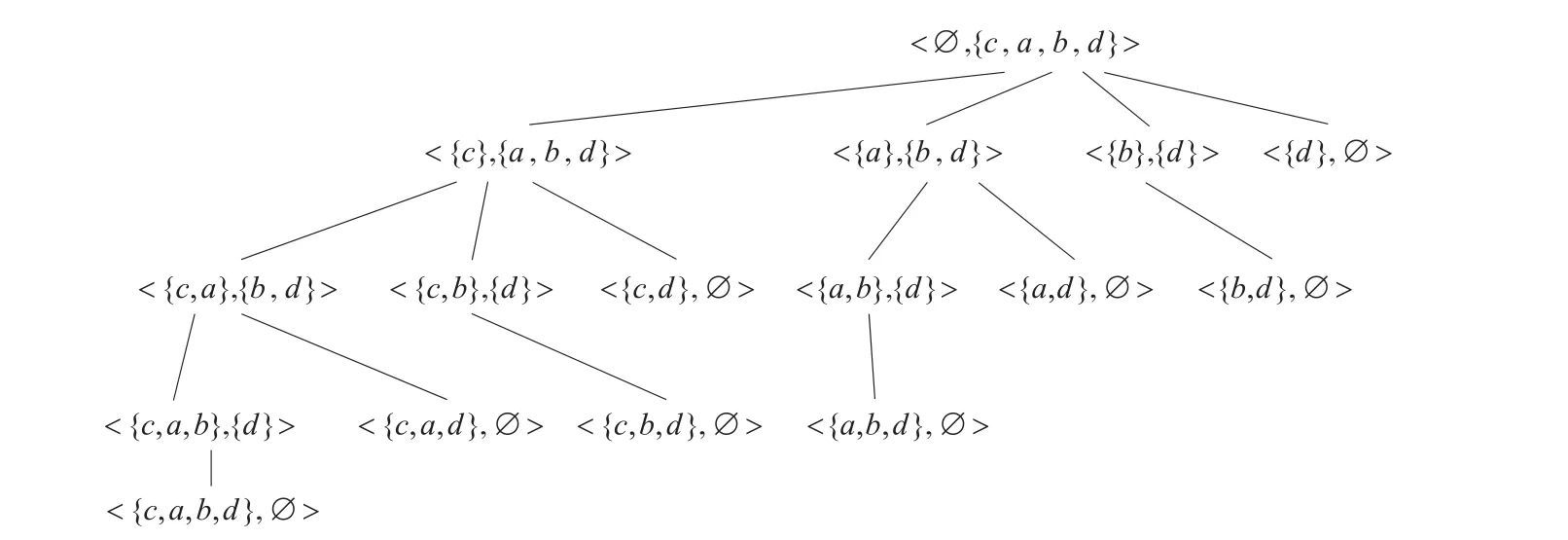
图1 集合{c，a，b，d}所对应的集合枚举树

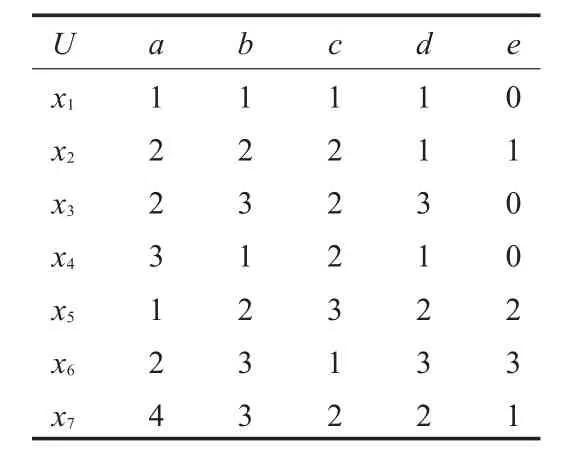
表1 某一决策表

定义1 在决策表 S=(U，C，D，V，f)中，∀R⊆C，决策属性 D的 R正域 POSR(D)定义为 POSR(D)=∪{Y∈U/R: Y∈U/D}。

定义2 设 S=(U，C，D，V，f)是一个决策表，P∈C，如果 POSC-{a}(D)=POSC(D)，则称a是C中不必要的（多余的）属性;否则，称a是C中必要的属性。

定义3设S=(U，C，D，V，f)是一个决策表，条件属性集C中所有必要的属性组成的集合，称为属性集C的核，记作Core(C)。

定义4 设 S=(U，C，D，V，f)是一个决策表，B⊆C是一个属性子集，如果满足

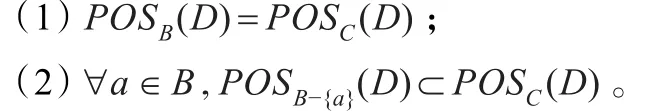
则称B是C的一个约简。

2 属性集上的序关系

属性重要度标示了属性在决策表中的重要性，粗糙集传统的属性重要度定义只区分属性对正域变换的影响，而没有考虑属性对于知识粒大小的影响，因此，结合这两方面考虑重新定义了属性重要度。

定义5 设 S=(U，C，D，V，f)是一个决策表，B⊆C是一个属性子集，属性集B的重要度为：

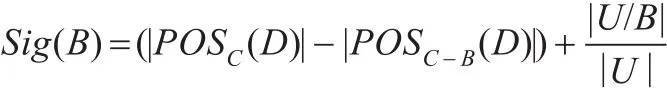
定理1 ∀a∈C，如果Sig({a})＞1,那么a∈Core(C)。

证明根 据 定 义5可 知 ，Sig({a})=(|POSC(D)|-由于0＜|U/{a}|/||U ≤1,那么|POSC(D)|-|POSC-{a}(D)|＞0,也即是说 POSC(D)≠POSC-{a}(D)。所以，属性a是必要属性。

定义 6 设 S=(U，C，D，V，f)是一个决策表，n=|C|。基于属性重要度定义条件属性集C上的序关系“≻”，从而可获得条件属性集C上的一个序列：a1≻a2≻…≻an，表示为Ordered(C)={a1，a2，…，an}， 则有 Sig({a1})≥ Sig({a2})≥… ≥Sig({an})。

3 集合枚举树

用图1所示的集合枚举树[15]来描述条件属性子集，通过枚举出所有的条件属性组合，使得求解最小属性约简的过程变成集合枚举树的搜索过程。图1表示了表1条件属性的集合枚举树，C={a，b，c，d}。树的每个节点由两部分组成，第一部分称为首（head），记做h(node)，由枚举树中当前节点的枚举属性集组成；第二部分称为尾（tail），记做t(node)，由当前节点的子节点的所有属性除去当前节点后所包含的属性排序而成。当前节点n的子节点nc生成方法为：h(nc)=h(n)∪{i}，i∈ t(n);t(nc)={j|j∈t(n)，i≻ j}。例如：对于节点 ＜{c}，{a，b，d}＞而言，有三个子节点 ＜{c，a}，{b，d}＞，＜{c，b}，{d}＞ 和 ＜{c，d}，ø ＞ 。

4 最小属性约简算法

为了找到决策表最小属性约简，采用简单的至上而下、层次优先搜索算法搜索集合枚举树，其搜索空间近似为条件属性幂集。为了减少搜索空间，提高算法效率，必须采用一定的剪枝策略。

4.1 属性核剪枝

因为所有的决策表属性约简必须包含属性核，所以可以剪去集合枚举树中不包含属性核的节点，如图1中的节点 ＜{a}，{b，d}＞等，因为它没有包含属性核{c}。根据属性核剪枝方法，可使集合枚举树的初始root节点为＜Core(C)，C-Core(C)＞，从而图1所示集合枚举树可剪枝为图2所示的集合枚举树。

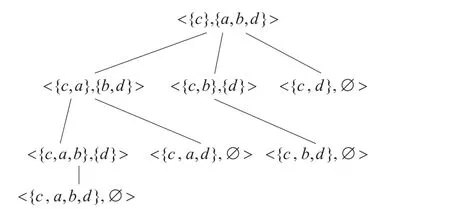
图2 图1剪去不含核属性{c}后的集合枚举树

4.2 父集剪枝

众所周知，若集合B(B⊆C)不是决策表的属性约简，则其任意子集都不是决策表属性约简。在集合枚举树中，若非叶子节点的h(node)∪t(node)不是决策表的一个属性约简，则可从集合枚举树中剪去以＜h(node)，t(node)＞为根节点的子树。

4.3 优化计算

根据集合枚举树的定义可知，非叶子节点和其最左边子树根节点的h∪t（节点首并节点尾）是相同集合，如＜{c，a}，{b，d}＞ 和其最左边子树根节点 ＜{c，a，b}，{d}＞，那么在父剪枝策略中，存在对同一个集合多次计算其正域是否等于POSC(D)。优化计算就是确保同一集合的正域只计算一次，从而提供算法效率。

5 算法描述及其伪代码

算法描述：函数 getSubNodes（Candidate Group g，Set of Candidate Group G）的功能是，若g是一叶子节点且其首h(g)的正域等于 POSC(D)，则节点g的首h(g)是决策表一最小约简；否则返回节点g的所有子节点。

6 实验结果

表2展现了核剪枝和父集剪枝减少算法搜索空间，同时也展示了优化计算提高算法的求解效率。该实验是基于Microsoft Visual C++6.0开发平台，操作系统Windows XP，CPU：Pentium III 1.73 MHz，内存768 MB仿真实现。

7 结束语

表2 基于UCI数据库仿真结果

本文提出了一种基于集合枚举树的最小属性约简完备算法，该算法把属性约简的计算问题转化为对集合枚举树的搜索式问题，以直观形象的方法展现了属性约简的过程，为属性约简问题的求解提供了一条新的途径。该算法提出了核和父集剪枝策略有效地减少了算法搜索空间；同时，基于优化计算提高了算法的运行效率。

[1]Pawlak Z.Rough sets[J].InternationalJournalofComputer and Information Science，1982，11（5）：341-356.

[2]SlowinskiR.Intelligentdecision support——handbook of applications and advances of the rough sets thorey[M].London：Kluwer Academic Publishers，1992.

[3]Wong S K M，Ziarko W.On optional decision rules in decision tables[J].Bulletin of Polish Academy of Sciences，1985，33（11/12）：693-696.

[4]Jelonek J.Rough set reduction of attributes and their domains forneuralnetworks[J].ComputationalIntelligence，1995，11（2）：339-347.

[5]Wang Jue，Miao Duoqian.Analysison attributereduction strategiesofrough set[J].JofComputSci& Technol，1998，13（2）：189-193.

[6]苗夺谦，胡桂荣.知识约简的一种启发式算法[J].计算机研究与发展，1999，36（6）：681-684.

[7]杨明，倪魏伟，孙志挥.一种新颖的最小属性约简模型[J].东南大学学报：自然科学版，2004，34（5）：604-608.

[8]刘文军，王加银，冯艳宾，等.一种求粗糙集中最小属性约简的新算法[J].北京师范大学学报：自然科学版，2004，40（1）：8-12.

[9]廖建坤，叶东毅.基于免疫粒子群优化的最小属性约简算法[J].计算机应用，2007，27（3）：550-552.

[10]Krysziewicz M，Lasek P.Fast discovery of minimal sets of attributes functionally determining a decision attribute[C]// InternationalConference on Rough Sets and Intelligent Systems Paradigms，2007：320-331.

[11]蒋瑜，王燮，叶振.基于差别矩阵的Rough集属性约简算法[J].系统仿真学报，2008，20（14）：3717-3720.

[12]Song Xiaoyu，Chang Chunguang，Liu Feng.Rough set theory based reduction algorithm fordecision table[C]//Proceedingsofthe 2009 InternationalConference on Machine Learning and Cybernetics，2009：2318-2323.

[13]Pawlak Z.Rough set-theoretical aspects of reasoning about data[M].Boston：Kluwer Academic Publishers，1991.

[14]张文修，吴伟志，梁吉业，等.粗糙集理论与方法[M].北京：科学出版社，2001.

[15]Rymon R.Search through systematic set enumeration[C]// Proc of 3rd Int’l Conf on Principles of Knowledge Representation and Reasoning，1992：539-550.

基于集合枚举树的最小属性约简算法

蒋 瑜

The purpose of this paper is to present an effective approach to achieve minimal attribute reduction.To achieve this goal,in this paper,it introduces a set-enumeration search tree by using total sequence over condition attribute set,and proposes a minimal attribute reduction algorithm,which uses the top-down level-first traversal to search set-enumeration search tree and guarantee that reduction discovered by it is a minimal reduction.To realize performance gains,this algorithm uses core and superset pruning to reduce search space,and uses optimal computing to guarantee that positive region of the same set only computes one time for reducing computing time.The experimental results with UCI data show that the proposed algorithm is effective.

rough set;minimal reduction;set enumeration search tree;attribute significance;pruning

为了寻找一种有效的最小属性约简方法，给出了条件属性集上的属性重要度序关系，基于此序关系构建了属性集上的集合枚举树，提出了一种快速的最小属性约简算法，该算法采用至上而下、层次优先策略搜索集合枚举树寻找属性最小约简。为了提高算法性能，该算法采用核和父集剪枝策略减少搜索空间，采用优化计算来确保同一集合的正域只计算一次。基于UCI数据的实验结果表明，该算法是有效的。

粗糙集；最小约简；集合枚举树；属性重要度；剪枝

A

TP311

10.3778/j.issn.1002-8331.1111-0416

JIANG Yu.Minimal attribute reduction for rough set based on set enumeration search tree.Computer Engineering and Applications,2013,49（11）：101-104.

蒋瑜（1980—），男，讲师，主要研究方向为粗糙集理论与数据挖掘。E-mail：jiangyu@cuit.edu.cn

2011-11-23

2012-01-10

1002-8331（2013）11-0101-04

CNKI出版日期：2012-04-25 http://www.cnki.net/kcms/detail/11.2127.TP.20120425.1719.034.html