CFD Simulation of Orifice Flow in Orifice-type Liquid Distributor

Yu Hongfeng; Li Xingang,; Sui Hong,; Li Hong,

(1. School of Chemical Engineering and Technology, Tianjin University, Tianjin 300072; 2. National Engineering Research Center of Distillation Technology, Tianjin 300072)

CFD Simulation of Orifice Flow in Orifice-type Liquid Distributor

Yu Hongfeng1; Li Xingang1,2; Sui Hong1,2; Li Hong1,2

(1. School of Chemical Engineering and Technology, Tianjin University, Tianjin 300072; 2. National Engineering Research Center of Distillation Technology, Tianjin 300072)

In this study, a suitable CFD (computational fluid dynamics) model has been developed to investigate the influence of liquid height on the discharge coefficient of the orifice-type liquid distributors. The orifice flow in different diameters and liquid heights has been realized using the shear stress transport (SST) turbulence model and the Gamma Theta transition (GTT) model. In the ANSYS CFX software, two models are used in conjunction with an automatic wall treatment which allows for a smooth shift from a wall function (WF) to a low turbulent-Renear wall formulation (LTRW). The results of the models coupled with LTRW are closer to the experimental results compared with the models with WF, indicating that LTRW is more appropriate for the prediction of boundary layer characteristics of orifice flow. Simulation results show that the flow conditions of orifices change with the variation of liquid height. With respect to the turbulence in orifice, the SST model coupled with LTRW is recommended. However, with respect to the transition to turbulence in orifice with an increase in liquid height, the predictions of GTT model coupled with LTRW are superior to those obtained using other models.

discharge coefficient; orifice-type liquid distributors; CFD; liquid height

1 Introduction

Uniform liquid distribution is essential to the efficient operation of petroleum, petrochemical and chemical processing equipment, such as packed columns[1]and tricklebed reactors[2]. Consequently, liquid distributors, which can provide a good initial liquid distribution state, are one of the most important internal components in these pieces of equipment. There are many different types and structures of liquid distributors, but the ori fice-type liquid distributors are widely used in industry, because they have the ability to operate over a broad range of liquid flow rates[3]and can be designed with a large amount of drip points (ori fices) to provide better liquid distribution[4].

To obtain an optimum distribution, proper consideration must be given to flow behavior in the liquid distributors. In the orifice-type liquid distributors, the orifice flow is the most important flow pattern because it directly affects the liquid distribution quality. Liquid flow through an ori fice is a common flow phenomenon in industry, and has been extensively investigated. Reader-Harris and coworkers[5-6]have derived an ori fice plate discharge coefficient equation based on the enlarged EEC/API database including the data collected in the 50-mm and 600-mm diameter pipes. An investigation[7]shows that discharge coef ficients of sharp-edged cylindrical ori fices are scaled with the Reynolds number and the aspect ratios in the attached flow regions are in fluenced by the diameter of the orifice in the attached and cavitated flow regions. Studies[8-9]on ori fices in pressurized pipes for lateral out flow show that the discharge coefficient is a function of approach velocity and the ratio of ori fice diameter to pipe diameter, in addition to the pressure in the pipe. Prohaska and co-workers[10]have investigated experimentally the discharge coef ficient for different circular ori fices in two different sizes of riser pipe. However, the results of these works, obtained from investigations of orifice flow in pipes, cannot be directly applied to researches on the orifice flow in the ori fice-type liquid distributors because the characteristics of two types of ori fice flow are different.

One of the main characteristics relating to the ori fice flowin the ori fice-type liquid distributors is that this type of ori fice flow is resulted from the hydrostatic pressure caused by the liquid height (see Figure 1), which is different from the ori fice flow in pipes. As a result, the liquid height becomes a very important factor in fluencing the ori fice flow in the ori fice-type liquid distributors. However, the available information on the investigation of the liquid height in fluence on this type of ori fice flow is very limited in the literature. Most importantly, by means of the change of liquid height, the ori fice-type liquid distributors can easily acquire the ability to operate over a broad range of liquid flow rates. Therefore, the investigation of the ori fice flow in the ori fice-type liquid distributors, in particular the influence of the liquid height on the discharge coef ficient, is useful for the design of the ori fice-type liquid distributors.

Figure 1 Schematic diagram of orifice flow in the orifice-type liquid distributors

Although experimental data are easily collected using water as the liquid phase, these data cannot be directly applied to the liquid, which has a different behaviour than water[11]. Additionally, experiments with other liquids are much more expensive. Compared to conventional experimental methods, the CFD methods can be done easily. For this reason, the most important objective of this study is to develop a suitable CFD model.

Modeling turbulent flow of orifices in the orifice-type liquid distributors represents a challenging task. For the flow at high Reynolds number, two-equation turbulence models[12]such as SST model[13]can be applied for investigation because of their economic effectiveness and accuracy for industrial flow simulations. For the transitional flow, these models cannot describe this type of flow and a transitional flow model should be adopted. Transitional flow models have been extensively investigated over the past few decades[14-16], however, most of these models are not applied in engineering CFD simulations. In this study, a Gamma Theta transition model[17]is applied to describe the transitional flow. Reasons for using this transition model are as follows: (a) This model is compatible with modern CFD methods using unstructured grids and massive parallel execution approach because it is based on local variables; (b) This model is proposed on the basis of the SST model and would not affect the underlying turbulence model in fully turbulent regimes. To sum up, the SST model and the GTT model are applied to investigate the orifice flow in the orifice-type liquid distributors.

2 Mathematical Models

2.1 Homogeneous multiphase flow

A homogeneous multiphase and free surface flow model[18]which is a limiting case of Eulerian-Eulerian multiphase flow model is applied in CFD simulations because two fluids (liquid and gas) in the orifice-type liquid distributors are separated by a distinct resolvable interface[11](see Figure 1). In this model[18-19], the two fluids (air and water) can be determined by solving a single set of governing transport equations.

The CFD simulation is based on numerical solutions of the steady state Reynolds averaged continuity and Navier-Stokes (RANS) equations. The governing equations based on the homogeneous multiphase flow model are listed below:

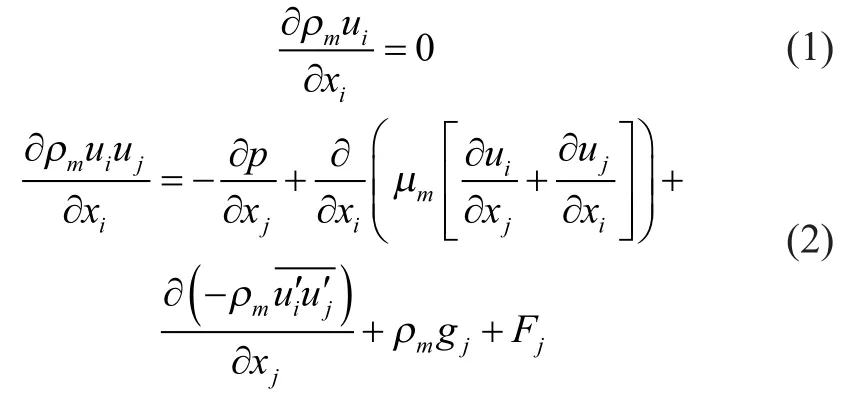
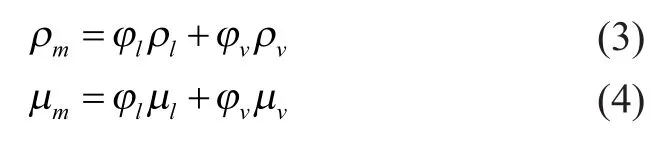
whereφlandφvare the volume fraction of liquid and gas, respectively;ρlandρvare the density of liquid and gas, respectively;μlandμvare the viscosity of liquid and gas, respectively.

2.2 Interface tracking method

To calculate the liquid height (see Figure 1), the interface of air and water should be accurately determined. Therefore, the volume of fluid (VOF) method[21-22]has been used to trace the interface of air and water. In this method[18,23], the volume fraction of liquid (φl) is determined throughout the flow field by solving a continuity equation which has the following form:

Because the present homogeneous multiphase system consists of air and water, the volume fraction of the gas phase (φv) can be obtained from:

2.3 Closure models

2.3.1 SST turbulence model

The shear stress transport (SST) turbulence model, which combines the advantages of thek-εmodel and thek-ωmodel, is used to close the RANS equations. It gives an improvement to the prediction of flow separation phenomenon in an adverse pressure gradient, because the influence of the transport of turbulent shear stress is taken into account[24-25]. The turbulent kinetic energykand turbulence frequencyωare calculated from their governing equations:

whereGkis the shear production of turbulence;F1is the blend function which is equal to zero away from the surface (k-εmodel), and switches over to one inside the boundary layer (k-ωmodel). The turbulent eddy viscosity is defined as follows:

whereSis the invariant measure of the strain rate, andF2is a second blending function.

2.3.2 Transition model

The Gamma Theta transition model is based on two transport equations, one for the intermittency and one for the transition onset criteria in terms of momentum thickness Reynolds number[26-27]. The two transport equations are formulated as follows:

Intermittency,γ:

Transition momentum thickness Reynolds number

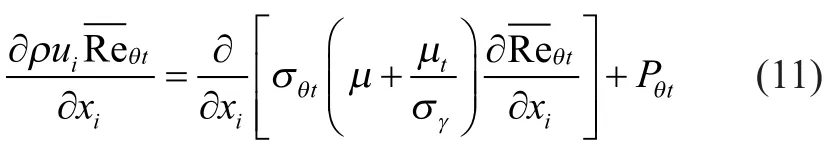
The Gamma Theta transition model has been calibrated for use with the SST turbulence model, which interacts with the turbulence model according to the following equations:

The final modification to the SST turbulence model is a change in the blending functionF1responsible for switching between thek-εandk-ωmodels. The modified blending functionF1newis defined as follows:

2.4 Numerical details

In the present study, numerical simulations were performed using the CFD commercial software ANSYS CFX. All governing equations were discretized using an element-based finite volume method[28]. For the SST turbulence model, the first order upwind schemeis used to discretize the turbulence equations. For the transition model, however, the numerical discretization method of transport equations should be set to the high resolution scheme[28]. The discretized RANS, pressure correction and volume fraction equations, together with the equations for turbulence model and transition model, were solved iteratively using a coupled algebraic multigrid method[28-29].

3 Experimental Set-up and Procedure

The experimental set-up is shown schematically in Figure 2. As shown in this figure, the experiments were carried out in a rectangular main channel, 730 mm in length, 150 mm in width, and 430 mm in depth. A bypass was designed to regulate the flow rate of water supplied to the main trough. Additionally, an overflow baffle was provided at the end of the main trough to control the liquid height in the main trough. In the experimental procedure, the most important point is that the overflow discharge is much less than the discharge of the orifice, which means that the influence of overflow can be neglected. Water was used as the working fluid in all experiments.

Figure 2 Schematic diagram of experimental set-up

Experiments were performed at an orifice diameterd= 4, 6, 8, 10, 12 and 16 mm, respectively. The wall thickness was 2 mm, and the orifices were made of perforated ones. The discharge coefficient,Cd, is calculated using the following relation:

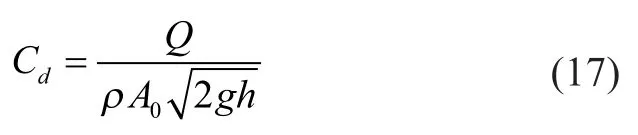
where Q is the measured value for the experiment or the calculated value for the CFD simulation,ρis liquid density,A0is the geometric orifice area,gis the gravity acceleration, andhis the liquid height. In the experiment, the value ofQand its corresponding liquid height h can be measured, respectively, by a weighing method and a ruler attached to the overflow baffle. The weighing method was implemented by measuring the weight of flow going out through the orifice in a certain period of time. In order to minimize experimental errors, the flow rate of each orifice was measured three times and the average measured data were used to validate the CFD simulation.

4 Computational Details

4.1 Computational domain

A typical computational domain is shown in Figure 3 (a), with the computational domain near the orifice and the orifice structure being presented in Figure 3 (b) and (c), respectively. In addition to the boundary conditions (at the inlet, opening and outlet) that are shown in Figure 3, the boundary conditions of other planes were set as walls. The no-slip velocity condition together with appropriate wall functions was applied to all walls. In conjunction with the SST model and the GTT model, an automatic wall treatment was employed, which allowed for a smooth shift from a low turbulent-Renear wall formulation (LTRW) to a wall function (WF) depending on the values ofy+, the dimensionless distance from the wall. The LTRW requires a near wall grid resolution of y+of at least ＜2. The physicochemical properties of water and air were determined at a temperature of 25 ℃ and a pressure of 1 atm. A relative pressure of 0 Pa was provided for the opening and outlet.

Figure 3 Illustration of computational domain

4.2 Computational mesh

As it has been mentioned previously, the automatic nearwall treatment can automatically switch from WF to LTRW depending on the values ofy+. Therefore, the computational domain was carried out on two meshes (i. e., coarse and fine). For the LTRW computations, the fine meshes were used to ensure thaty+would fall below 2.On the contrary, the coarse meshes were used for the WF. A strategy of mesh generation is illustrated in Figure 4 and Figure 5. As shown in Figure 4, the computational domain was carried out on unstructured meshes. To accurately describe the ori fice flow, a re fined mesh (Figure 5) was applied to the flow domain in and around the ori fice. The unstructured meshes were made up of prismatic elements (Figure 5c) employed to resolve the boundary layer of the ori fice wall and the tetrahedral elements covering the rest of the domain. Two meshes (coarse and fine) had the same strategy of grid generation, and the fine meshes differed from the coarse ones thanks to the improved refinement of the near wall grid resolution for the domain in and around the ori fice.

4.3 Mesh independence

Mesh independence tests were carried out to establish the effect of mesh size on the calculated results. As it has been mentioned previously, the coarse and fine meshes were applied in the CFD simulation, therefore, mesh independence tests were carried out for each mesh. For example, in the case of simulating a liquid height of 100 mm along with an orifice having a diameter of 4 mm, CFD simulations were performed with seven mesh sizes consisting of 3.4×105, 5.2×105, 8.1×105, 13.2×105, 44.1×105, 55.7×106and 69.8×105cells, respectively, to examine the effect of mesh size on the solution. Among the seven mesh sizes, the first four were used in the simulations for the WF case and the rest were used in the simulations for the LTRW case. The discharge coefficient obtained from calculations using a mesh size of 8.1×105cells was nearly identical to that obtained using a mesh size of 13.2×105cells. Therefore, for the orifice with a diameter of 4 mm, the mesh size consisting of 8.1×105cells was used in all further simulations for the WF case of orifice with a diameter of 4 mm. Similarly, the mesh size consisting of 55.7×106cells was used in all further simulations for the LTRW case of orifice with a diameter of 4 mm, because the simulated discharge coefficient of this mesh was nearly identical to that obtained using a mesh size of 69.8×105cells. A similar procedure was used to determine the most suitable mesh size for the CFD simulations of other orifices.

Figure 4 Computational mesh

Figure 5 Illustration of refined mesh

5 Results and Discussion

5.1 Results of experiments

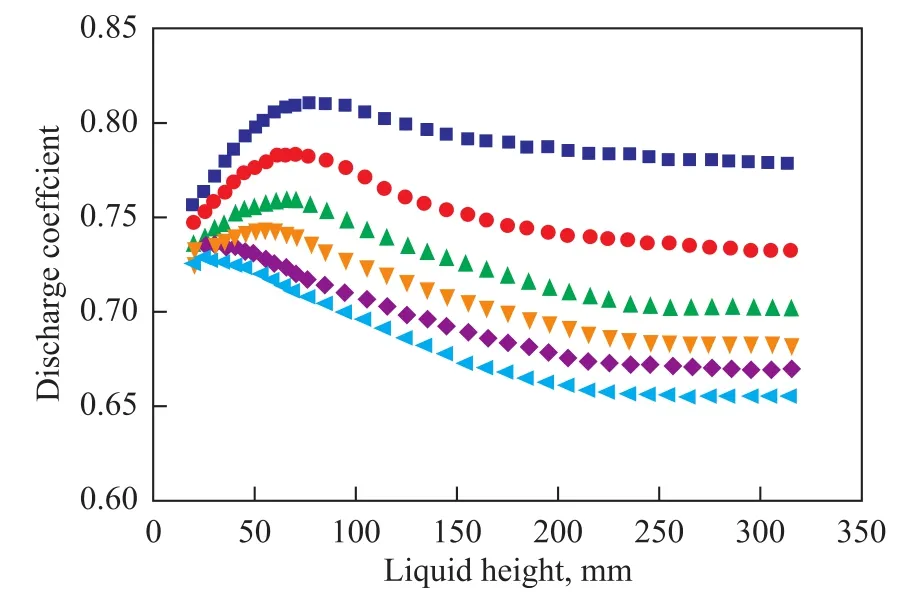
Figure 6 Variations of the discharge coefficient with the liquid height

The variations of the discharge coefficient with the liquid height are shown in Figure 6. The first observation is thatthe value of the discharge coefficient in most cases decreases with a decreasing orifice diameter. Figure 6 also shows that variations of the discharge coefficient with an increasing liquid height are different because of different aspect ratios of orifices[5～7,30]. For the orifices with larger aspect ratio (with a diameter of 4 mm, 6 mm, 8 mm and 10 mm, respectively), the discharge coefficient first increases and then decreases with an increasing liquid height. For the orifices with smaller aspect ratio (with a diameter of 12 mm and 16 mm, respectively), the discharge coefficient decreases as the liquid height rises. Experimental results showed that the influence of liquid height on the discharge coefficient is complicated; therefore, further researches using CFD simulation were carried out in the following subsection.

5.2 Comparison between predicted and measured discharge coefficients

The predicted and measured discharge coefficients are shown in Figure 7. The discharge coefficients of orifice are calculated using the shear stress transport (SST) turbulence model and the Gamma Theta transition (GTT)model. As it has been mentioned before, two models are coupled with the automatic near-wall treatment which automatically switches from WF to LTRW depending on the values ofy+.

Figure 7 Predicted and measured discharge coefficients

It can be seen from Figure 7 that for the orifice with a diameter of 4 mm and 6 mm, respectively, the performance of the transition models is significantly better than that of the SST turbulence models. With the increase in diameter and liquid height, the results of SST turbulence models gradually approach those of transition models. A comparison between the calculated and experimental results also shows that the models coupled with the LTRW are closer to the experiments as compared to the models coupled with the WF. It indicates that the LTRW can provide better predictions for the flow in the near-wall region as compared with the case of WF, but it requires a very fine mesh in the near-wall zone and correspondingly a large amount of computational load and time. For the orifices with smaller diameter, especially the orifices with a diameter of 4 mm and 6 mm, respectively, the performance of GTT model coupled with the LTRW is significantly better than that of other models. For the orifices with larger diameter (viz., 12 mm and 16 mm), the performance of GTT model coupled with the LTRW is very similar to that of the SST model coupled with the LTRW.

5.3 Influence of liquid height

The predicted velocity fields in orifices for different diameters and liquid heights are shown in Figure 8. It can be seen from Figure 8 that the velocity fields of orifices with a diameter of 4 mm and 8 mm are predicted by the GTT model coupled with the LTRW and the velocity fields of orifice with a diameter of 16 mm are predicted by SST model coupled with the LTRW. The pictures in Figure 8 show that the velocity fields obtained at different orifice diameters and liquid heights are similar and the boundary layer separation at point A is an important influencing factor of velocity distribution in orifices. As a result, the performance of models coupled with the LTRW is better thanthat of models coupled with the WF because the boundary layer separation caused by sharp-edged contours needs a very fine mesh in the near-wall zone to describe the flow characteristics of boundary layer.

Figure 8 Predicted velocity fields of XY section (Z=365 mm) in orifices for different diameters and liquid heights

The Reynolds number of flow in the orifice presented in Figure 8 can be calculated using the following relation:

whereρis the liquid density, D is the diameter of orifices,Vis the liquid velocity,μis the liquid viscosity, g is the gravity acceleration, and h is the liquid height. According to the equation (18), the Reynolds number of the orifice flow increases with an increasing orifice diameter and liquid height. Ranges of the Reynolds number with the increase of the orifice diameter and the liquid height are listed in Table 1.

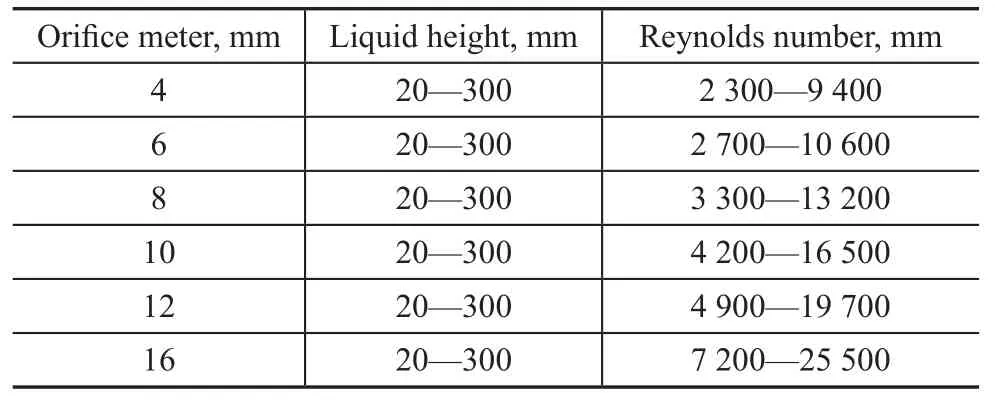
Table 1 Ranges of Reynolds number

According to ranges of Reynolds number[30]applicable to the orifice with small diameter, in the case of an orifice diameter of 4 mm the transitional orifice flow at a low liquid height can gradually develop into turbulence with an increase in liquid height; therefore, the performance of the transition models is significantly better than that of the SST turbulence models. For the orifice with larger diameter, for example in the case of an orifice diameter of 16 mm, the state of turbulence flow in the orifice can gradually develop into turbulence at higher Reynolds number with the increase in liquid height; therefore, the results of SST turbulence models are very similar to those of transition models. Additionally, the boundary layer separation caused by sharp-edged contours needs a very fine mesh in the near-wall zone. As a result, the GTT model coupled with LTRW should be used for simulating the transition to turbulence in the orifices; and the SST model coupled with LTRW could be recommended for the simulation of turbulence in the orifices. To sum up, the flow conditions of orifices change with the variation of liquid height, which is more important for the design of liquid distributors of small-diameter orifices that are more widely used in petroleum, petrochemical and chemical industries compared with liquid distributors of large-diameter orifices.

6 Conclusions

In this study, the homogeneous multiphase model, the VOF method, the shear stress transport (SST) turbulence model and the Gamma Theta transition (GTT) model were applied to describe the orifice flow in the orificetype liquid distributors. In the commercial CFD software ANSYS CFX, the SST model and GTT model are in conjunction with the automatic wall treatment which blends the standard log-law wall function (WF) to the low turbulent-Renear wall formulation (LTRW) depending on the values ofy+, a dimensionless distance from the wall.

Comparison between the simulated and the experimental results shows that the models coupled with the LTRW are more appropriate for the prediction of orifice flow compared with the models in combination with WF, which means that characteristics of boundary layer of orifice flow need a very fine mesh in the near-wall zone to describe. Analyses based on the orifice Reynolds number show that the flow conditions in orifices change with the variations of liquid height. The GTT model coupled with LTRW should be used for simulating the transition to turbulence in the orifices; and the SST model coupled with LTRW could be recommended for the simulation of turbulence in the orifices.

Acknowledgement:The authors are grateful for the financial support from the National Basic Research Program of China (No. 2009CB219905), the Program for Changjiang Scholars and Innovative Research Team in University (No. IRT0936) and the National Natural Science Foundation of China (No. 21176172).

[1] Perry D, Nutter D E, Hale A. Liquid distribution for optimum packing performance [J]. Chem Eng Prog, 1990, 86(1): 30-35

[2] Maiti R N, Nigam K D P. Gas-liquid distributors for tricklebed reactors: A review [J]. Ind Eng Chem Res, 2007, 46(19): 6164-6182

[3] Ranade V V, Raghunath V, Chaudhari R V, et al. Trickle Bed Reactors: Reactor Engineering & Applications [M]. Amsterdam: Elsevier, 2011

[4] Kister H Z. Distillation Operation [M]. New York: Mc-Graw-Hill, 1990

[5] Reader-Harris M J, Sattary J A. The orifice plate discharge coefficient equation [J]. Flow Meas Instrum, 1990, 1(2): 67-76

[6] Reader-Harris M J, Sattary J A, Spearman E P. The orifice plate discharge coefficient equation-further work [J]. Flow Meas Instrum, 1995, 6(2): 101-114

[7] Ramamurthi K, Nandakumar K. Characteristics of flow through small sharp-edged cylindrical orifices [J]. Flow Meas Instrum, 1999, 10(3): 133-143

[8] Gregg W B, Werth D E, Frizzell C. Determination of discharge coefficients for hydraulic sparger design [J]. ASME J Pressure Vessel Technol, 2003, 126(3): 354-359.

[9] Werth D E, Khan A A, Gregg W B. Experimental study of wall curvature and bypass flow effects on orifice discharge coefficients [J]. Exp Fluids, 2005, 39(3): 485-491.

[10] Prohaska P D, Khan A A, Kaye N B. Investigation of flow through orifices in riser pipes [J]. J Irrig Drain E-ASCE, 2010, 136(5): 340-347

[11] Heggemann M, Hirschberg S, Spiegel L, et al. CFD simulation and experimental validation of fluid flow in liquid distributors [J]. Chem Eng Res Des, 2007, 85(1): 59-64

[12] Schiestel R. Modeling and Simulation of Turbulent Flows [M]. Hoboken: John Wiley & Sons Inc, 2008

[13] Menter F R. Review of the shear stress transport turbulence model experience from an industrial perspective [J]. Int J Comput Fluid D, 2009, 23(4): 305-316

[14] Wilcox D C W. Simulation of transition with a two-equation turbulence model [J]. AIAA J, 1994, 32(2): 247-255

[15] Stock H W, Haase W. Navier–Stokes airfoil computations with eNtransition prediction including transitional flow regions [J]. AIAA J, 2000, 38(11): 2059-2066

[16] Suzen Y B, Huang P G. Modeling of flow transition using an intermittency transport equation [J]. J Fluids Eng, 2000, 122(2): 273-284

[17] Menter F R, Langtry R, Völker S. Transition modeling for general purpose CFD codes [J]. Flow Turbul Combust, 2006, 77(1/4): 277-303

[18] Haque J N, Mahmud T, Roberts K J. Modeling turbulent flows with free-surface in unbaffled agitated vessels [J]. Ind Eng Chem Res, 2006, 45(8): 2881-2891.

[19] Pineda S F, Blanco A J, Rojas-Solórzano L. CFD software applications for transcritical free surface flow [C]. ASME 2009 Fluids Engineering Division Summer Meeting, 2009, 1987-1994

[20] Brackbill J U, Kothe D B, Zemach C. A continuum method for modeling surface tension [J]. J Comput Phys, 1992, 100(2): 335-354

[21] Hirt C, Nicholls B. Volume of fluid (VOF) method for the dynamics of free boundaries [J]. J Comp Phys, 1981, 39(1): 201-225

[22] Wachem B G M, Almstedt A E. Methods for multiphase computational fluid dynamics [J]. Chem Eng J, 2003, 96(1/3): 81-98

[23] Mahmuda T, Haquea J N, Robertsa, K J. Measurements and modeling of free-surface turbulent flows induced by a magnetic stirrer in an unbaffled stirred tank reactor [J]. Chem Eng Sci, 2009, 64(20): 4197-4209

[24] Menter F R. Review of the shear stress transport turbulence model experience from an industrial perspective [J]. Int J Comput Fluid D, 2009, 23(4): 305-316

[25] Meslem A, Dia A, Beghein C. A comparison of three turbulence models for the prediction of parallel lobed jets in perforated panel optimization [J]. Build Environ, 2011, 46(11): 2203-2219

[26] Menter F R, Langtry R B, Likki S R, et al. A correlationbased transition model using local variables -- part I: model formulation [J]. J Turbomach, 2006, 128(3): 413-422

[27] Langtry R B, Menter F R, Likki S R, et al. A correlationbased transition model using local variables. Part II: Test cases and industrial applications [J]. J Turbomach, 2006, 128(3): 423-434

[28] ANSYS CFX-Solver Theory Guide [M]. Release 12.1, ANSYS Inc, 2009

[29] Stuben K. A review of algebraic multigrid [J]. J Comput Appl Math, 2001, 128(1/2): 281-309

[30] Cao R, Liu Y S, Yan C Y, et al. Characteristics of vertical sharp-edged orifice discharge: (I) Effect of flow regime and configuration parameters on orifice discharge coefficient[J]. J Chin Inst Chem Eng, 2008, 59(9): 2175-2180 (in Chinese)

[31] White F M. Fluid Mechanics [M]. Beijing: Tsinghua University Press, 2004

Recieved date: 2013-01-28; Accepted date: 2013-07-01.

Dr. Li Hong, Telephone: +86-22-87402119; E-mail: lihongtju@tju.edu.cn.