大气扰动下运输机空投过程建模与仿真分析

刘日，孙秀霞，董文瀚，李大东

（空军工程大学航空航天工程学院，陕西西安 710038）

0 引言

运输机空投主要指利用降落伞等动力减速器从大中型运输机上将货物空投至指定区域。目前对运输机空投过程的研究主要集中在空投建模［1-2］、操稳特性分析以及控制律设计［3］等。合理准确的模型是研究空投问题的基础，文献［1］采用矢量法，建立了飞机的全量动力学方程；文献［2］采用分离体法，将货物运动作为扰动项，加入到载机的运动方程中。值得注意的是，上述两种建模方法均未考虑风场的影响。而国内外大量的空投飞行过程及一些风洞试验表明，空投区域风场对空投过程将产生较大影响［4］。具体体现在:在空投阶段，货物的持续移动及瞬间离机将对载机产生较大干扰，尤其是空投重型货物，将使载机飞行状态严重偏离。复杂大气扰动会进一步恶化载机的动态性能，危及载机安全。因此，针对复杂大气环境下的空投过程建模及特性分析具有重要意义。

另一方面，在研究复杂大气扰动下的飞行力学问题时，常规建模方法普遍忽略风速沿机身和翼展方向的非均匀分布造成的附加气动力作用，即风速梯度效应［5］。但是，大中型运输机尺度与中小规模风场尺度可比，其沿机身和翼展方向不同点上所受的风速矢量不同［6-7］，由此造成飞机六自由度状态发生显著变化，此时必须考虑风速梯度效应。

本文主要针对大气紊流扰动下的空投过程进行建模，当考虑阵风、风切变等其他复杂大气扰动时，类似的方法仍可采用，模型具有较强拓展性。首先系统推导了无扰动风影响运输机空投货物舱内移动过程中的动力学方程；分析紊流风场对飞机的影响，提炼出紊流影响的平动和梯度效应，依此建立扰动风影响下空投过程动力学模型，提出气动参数修正的一般方法；最后以某型运输机为算例进行数值仿真，并对结果进行分析。

1 无扰动风时空投过程建模

基于文献［8］，分别定义地理坐标系Ogxgygzg，机体坐标系Obxbybzb，Og为地理系原点，Ob为空机质心，如图1所示。基本假设为:（1）将地球视为惯性系；（2）将飞机视为刚体；（3）将货物视为质点；（4）舱内导轨与机体轴Obxb重合。

图1 建模示意图

1.1 力方程推导

飞机绝对速度Vg，空速V和风速W三者形成速度三角形，关系为:

无风情形下，Vg=V。图1中有矢量关系:

由矢量的绝对导数与相对导数微分公式，两次微分整理得:

全机的总动量Φ=mbVg+mcVc，mb和mc分别为空机质量、货物质量。若FA代表作用在飞机上的气动力和推力的总矢量，由动量定理有:

由式（3）和式（4）得:

其中:

机体坐标系下Vg=［ug，vg，wg］T，Ω=［p，q，r］T，rcb=［－rcb，0，0］T，g=Mbg［0，0，g］T，FA=［X，Y，Z］T，Mbg为地理系到机体系的欧拉矩阵［8］。则机体坐标系下力方程（式（5））可表达为:

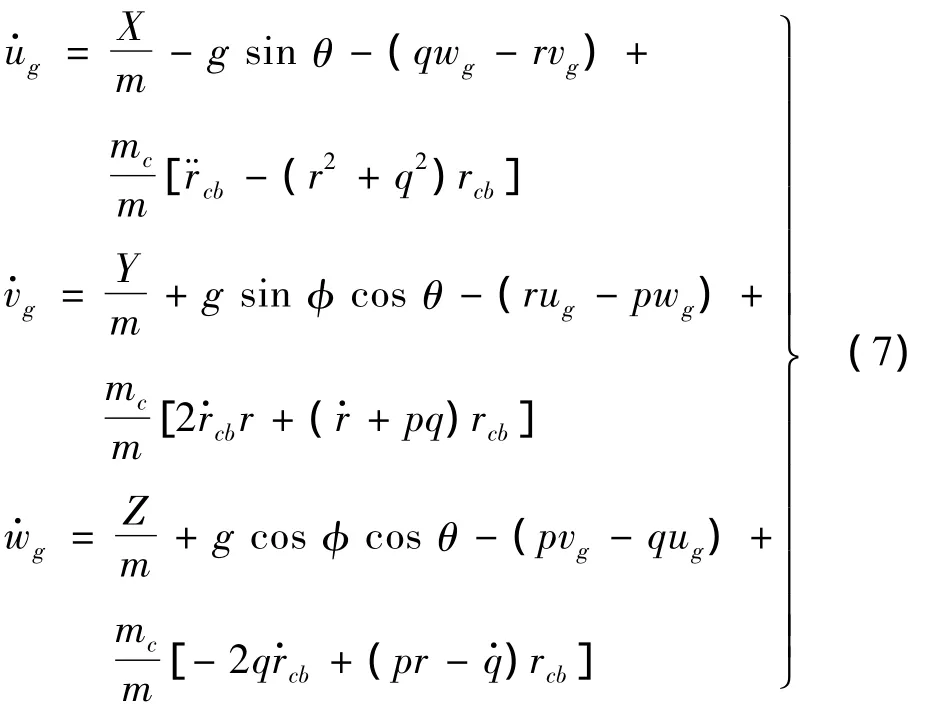
式中，m=mb+mc；θ，φ分别为飞机俯仰角、滚转角。

1.2 力矩方程推导

全机对惯性系原点Og的动量矩HT，包括空机动量矩和货物动量矩两部分:

式中，Hb为刚体飞机对质心的动量矩；mbr×Vg为飞机视作质点时对Og的动量矩；mcrc×Vc为货物对Og的动量矩。

由全机所受外力及力矩分析，易知全机相对惯性坐标系原点的总力矩MT包括FA，mbg，mcg相对惯性系原点Og产生的力矩及FA对空机质心Ob产生的力矩MB，即:

由动量矩定理:

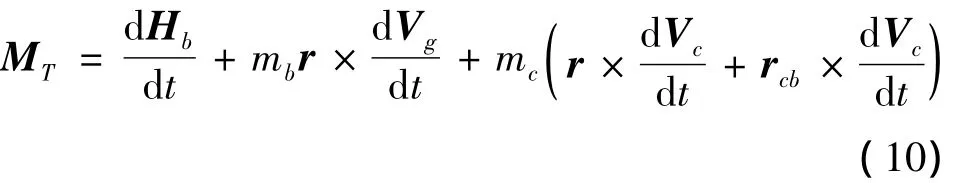
由式（3）、式（4）和式（9）知，式（10）可化为:

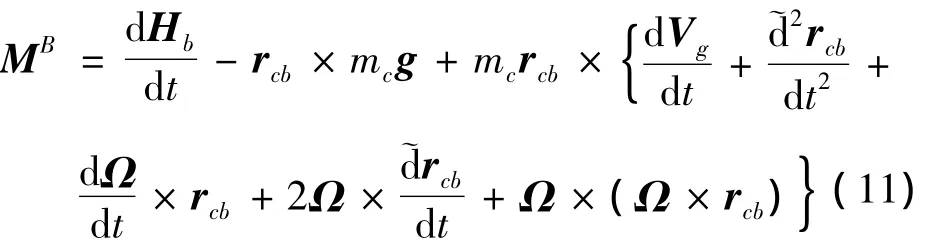
其中:

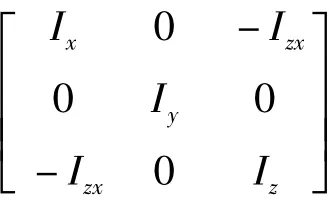
2 引入风效应的空投过程建模

2.1 大气紊流对飞机影响分析

在某一轴向紊流物理特性可由风速和沿该轴风速变化来描述［8-9］。因此，紊流的空气动力效应可以归结为:（1）平动效应。即风速对飞行速度V、迎角α和α·、侧滑角β和β·的影响；（2）梯度效应。风速沿机体的非均匀分布造成的附加气动作用。风速对V的影响可显式表达在力和力矩方程中。风速对α，α·，β和β·的影响，以及风速的梯度效应，本质上是对飞机相关气动参数的修正。关于紊流模型描述可参见文献［8-9］。

2.2 引入风速平动效应的方程推导

假设空间任一点风速矢量Wb=［uwb，vwb，wwb］T。将式（1）及其微分形式代入式（7）和式（13）中，推导出机体系下含扰动风影响的力方程为:

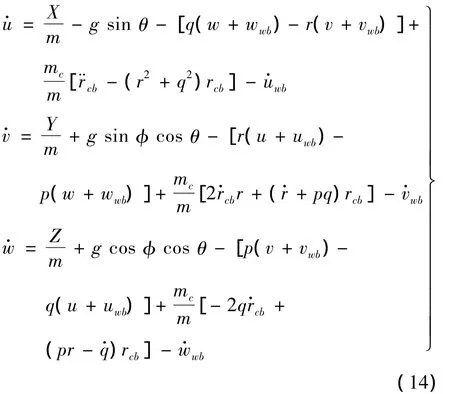
力矩方程为:

扰动风矢量一般是基于地理坐标系给出的W=［uw，vw，ww］T。对于式（14）和式（15），需将地理系下的风速矢量进行坐标变换:

对式（16）求导得:

式中，Τ为斜对称矩阵。将式（18）代入式（17）得:

将式（16）、式（19）代入式（14）、式（15）可得含扰动风影响的空投过程动力学模型。

风速的平动效应对飞行速度V的影响已显式表达在动力学方程中。由α，β计算公式［［8］:

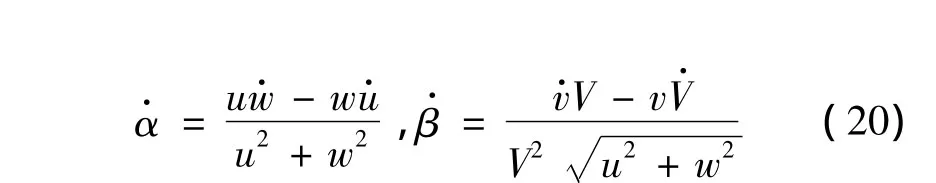
2.3 引入风速梯度效应的模型修正

风速梯度效应可通过飞机相对于空气的角速度ΩA=［pA，qA，rA］T的相关导数修正。

式中，Ωw=［pw，qw，rw］T为风的角速度，它是由风速梯度wwy=∂ww/∂y，vwz= ∂vw/∂z等造成的:

将ΩA引入相关气动导数，即完成风速梯度效应影响下的模型修正。以滚转力矩系数Cl为例，Cl=Clp［p－（wwy－vwz）］b/2V+Clr［r－ （vwx－uwy）］b/2V…，符号定义参见文献［8］。

3 仿真算例及结果分析

3.1 纵向响应分析

分别对无紊流扰动、紊流强度为4 m/s和6 m/s三种情形下空投过程载机纵向响应进行仿真比较。结果如图2所示。

由图2可知，扰动风影响下q峰值、α峰值明显高出无扰动情形，且扰动风越强，q，α振荡峰值越大，动态性能越差。由此推知，强扰动风将严重影响载机阻尼特性、稳定性，危及载机安全。

图2 纵向运动参数响应曲线

3.2 横航向响应分析

在3.1节的仿真情形下比较空投过程载机横侧向响应。结果如图3所示。

图3 横航向运动参数响应曲线

由图3可知，有扰动风时，p，r及β的振荡反映了载机横航向阻尼特性、稳定性变差。货物离机前，载机横航向运动对紊流的响应均是较小幅值，货物离机后横航向各运动参数振荡幅值均逐渐增大，且扰动风越强，振荡幅值越大。可见，货物瞬间离机，引起载机惯性量阶跃变化，加剧载机对扰动风的响应。

3.3 引入风速梯度模型与常规质点模型对比

紊流强度均设置为4 m/s，针对建模过程中引入风梯度效应与常规飞机质点模型（即不考虑风速梯度效应）进行仿真对比，结果如图4所示。图中曲线表示两种建模方法下空投过程载机运动参数响应差值。

图4 气流角动态响应差值

由图4可知，Δα，Δβ振荡峰值均约0.02 rad。上述差值明显不能忽略，因此研究大型飞机遭遇紊流场的响应问题必须考虑风速梯度效应。

4 结束语

大量的空投飞行试验证明，复杂的大气扰动将对空投过程产生较大影响。而目前尚无文献就该问题进行数学建模与理论推导。本文基于矢量法详细推导了复杂大气扰动下运输机空投过程动力学模型。改进了常规基于“飞机质点模型”的建模方法，通过对飞机气动导数修正将风速的梯度效应引入空投过程非线性模型。以某型运输机为例，通过数值仿真的方法对复杂大气扰动对空投过程的影响进行了定量研究，进一步探索了大气扰动对空投过程影响的理论根源。建立的模型更贴近空投实际，为综合运用数值仿真、半实物仿真的方法研究运输机空投问题奠定了理论基础，并为空投载机控制律设计提供参考。

［1］Chen Jie，Shi Zhongke.Aircraft modeling and simulation with cargo moving inside［J］.Chinese Journal of Aeronautics，2009，22（1）:191-197.

［2］欧阳绍修，丁重舜.货物在货舱内移动时飞机动态特性的研究［J］.飞行力学，1992，10（1）:77-86.

［3］Zhang Huiyuan，Shi Zhongke.Variable structure control of catastrophic course in airdropping heavy cargo［J］.Chinese Journal of Aeronautics，2009，22（2）:520-527.

［4］Yannick Bury，Scott A Morton，Richard Charles.Experimental investigation of the flow field in the close wake of a simplified C-130 shape a model approach of airflow influence on airdrop［C］//Proceedings of 26th AIAA Applied Aerodynamics Conference.USA:2008:1-20.

［5］Ray C Chang，Ye C E.Flying qualities for a twin-jet transport in serve atmospheric turbulence［J］.Journal of Aircraft，2009，46（5）:1673-1680.

［6］Crimaldi J P，Britt R T，Rodden W P.Response of B-2 aircraft to nonuniform spanwise turbulence［J］.Journal of Aircraft，1993，30（5）:652-659.

［7］Camp D W，Campbell W，Dow C.Visualization of gust gradients and aircraft response as measured by the NASA B-57B aircraft［C］//Proceedings of 22nd AIAA Aerospace Sciences Meeting.USA:1984:1-4.

［8］鲁道夫·布罗克豪斯.飞行控制［M］.金长江，译.北京:国防工业出版社，2007:68-71.

［9］肖业伦，金长江.大气扰动中的飞行原理［M］.第1版.北京:国防工业出版社，1993:47-72.