解读导数背景下的“参数分离”

☉江苏省丹阳高级中学 陈曦远

含参变量的不等式恒成立问题是历年高考的热点，也是难点，在各省市高考命题中屡见不鲜，且常考常新.此类问题综合性较强，融函数、导数、不等式等高中数学主干知识为一体，能有效考查考生的综合解题能力，在培养学生思维的灵活性、创造性方面起到了举足轻重的作用.在众多的求解方法中“分离参数”法的作用不容忽视.本文以导数背景下的不等式恒成立问题为例，谈谈“分离参数”法的应用.

一、参数的直接分离

例1 已知函数f（x）=lnx-ax+1，a∈R是常数.讨论函数y=f（x）零点的个数.

当x=1时，g（x）的最大值为g（1）=1.

所以若a＞1，则f（x）无零点；

若f（x）有零点，则a≤1.

若a=1，f（x）=lnx-ax+1=0，易知f（x）有且仅有一个零点x=1.

若a≤0，f（x）=lnx-ax+1单调递增，由幂函数与对数函数的单调性比较，知f（x）有且仅有一个零点（或：直线y=ax-1与曲线y=lnx有一个交点）.

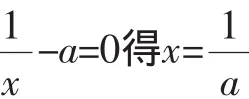
综上所述，当a＞1时，f（x）无零点；当a=1或a≤0时，f（x）有且仅有一个零点；当0＜a＜1时，f（x）有两个零点.

点评：本题原为考查零点的个数问题，经参数直接分离后即转化为函数与直线交点个数问题，进而使问题轻松获解.

二、导函数中的参数分离

例2 已知函数f（x）=x2+2alnx.

（1）求函数f（x）的单调区间；

解析：（1）略.

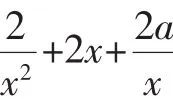
点评：题目中若给出函数在某区间内的单调性，则问题转化为导函数在该区间内恒大于（小于）0，进而再进行参数分离求解即可.

三、整体思想下的参数分离

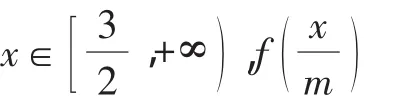
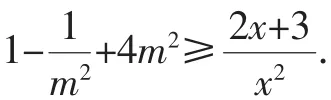
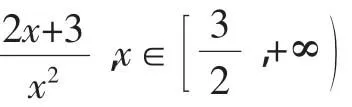
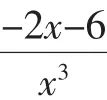
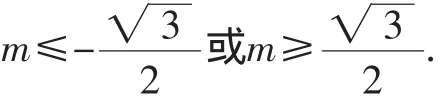
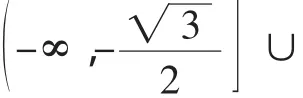
点评：分离出来的参数，有些时候并不是以单独的字母的形式出现，而是一个关于参数的函数式g（m），如g（m）≤f（x）或g（m）≥f（x）的形式，解题思路是先求出f（x）在给定的区间上的最值，即有g（m）≤fmin（x），g（m）≥fmax（x）.

四、自变量的取值范围决定了参数是否能顺利分离

例4 设函数f（x）=ax3-3x+1，（x∈R），若对任意的x∈［-1，1］，都有f（x）≥0成立，则实数a的值为______.

解析：由ax3-3x+1≥0，得ax3≥3x-1.因x∈R，故分离参数a，需根据x的取值进行分类讨论，如下：

（1）当x=0时，f（x）=1＞0恒成立，a可以取任意实数；

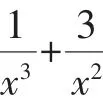
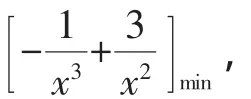
综上可得a=4.

点评：本题在参数分离的过程中，要在不等式两边同时除以x才能实现参数的分离，若x的取值范围在正数区间上，可以避免讨论；若x的取值范围中包含零或者负数，则需要进行分类讨论.

五、函数最值的存在性决定参数取值区间的开或闭

A.［-1，+∞）B.（-1，+∞）C.（-∞，-1］D.（-∞，-1）

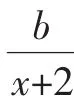
函数g（x）=x（x+2）在区间（-1，+∞）上的值域为（-1，+∞），不存在最小值-1，故b的值可以为-1，即b≤-1，答案为C.

例6 已知函数f（x）=x2-3x，当x∈（0，+∞）时，不等式f（x）＞ax-1恒成立，则实数a的取值范围为__________.

点评：参数的取值范围必然涉及区间的开或闭，起决定因素的是不等号以及函数最值的存在性.比如a≤f（x），f（x）的最小值是fmin（x），则a≤fmin（x）；当f（x）没有最小值，但接近一个常数m，则a≤m.又如a＜f（x），f（x）的最小值是fmin（x），则a＜fmin（x）；当f（x）没有最小值，但接近一个常数m，则a≤m.

综上所述，本文简述了解不等式恒成立问题中“分离参数”法的应用，此法是求解不等式“恒成立”问题的基本应对策略.教师在实际教学中还应注重培养学生对解题方法的提炼，经常引导学生梳理知识，形成知识板块和方法体系，真正提高学生分析问题和解决问题的能力.