无缝的对接 “双动”的精彩 优雅的解法

☉湖北省阳新县高级中学 邹生书

从这道预赛试题笔者很快联想到如下两道经典考题：

而上述两道考题分别基于如下两个重要结论：

结论1：到两个定点的距离之比为定值（不为1）的点的轨迹是一个圆，这个圆叫做阿波罗尼斯圆.

对于上述两题的研究文章颇多，解法也较多，本赛题就是这两道试题或上述两个结论的富有创造性的完美结合，因此解法也较多，本文笔者用向量、均值不等式和轨迹与方程给出一个优雅的解法以飨读者.

解：如图1，延长AG交BC于点D，则点D为边BC之中点.

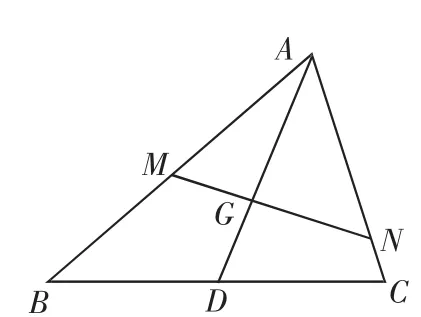
图1

图2

由此可见命题者真可谓匠心独运，以三角形重心和阿波罗尼斯圆为背景，通过“求四边形MNCB的面积的最大值”这一问题将希望杯竞赛题和江苏高考题巧妙地合二为一，对接得天衣无缝、浑然一体，用双动态、双最值求面积最大值，使得问题不仅上档次综合性强，而且有文化背景，能演绎数学精彩、体现数学美，本文解法也可算是优美而高雅.

1.王建荣，吴芳.解读二十二届希望杯高二第一试的一道最小值问题［J］.中学生数学（上），2011（9）.

2.阮灵东.也谈二十二届希望杯的一道竞赛题［J］.中学生数学（上），2012（7）.

3.曾晓阳.再谈一道二十二届希望杯赛题.中学生数学（上），2013（4）.

4.徐勇.江苏卷理科第13题［J］.数理天地（高中版），2008（10）.

5.於升贤，等.2008年江苏卷理科第13题的两种解法［J］.中学生数学（上），2009（11）.