众里寻它千百度，那“题”却在“教材”处——一道数学模拟试题的命制历程及感想

☉江苏省通州高级中学 马 进

教材中例题和习题是高考和模拟试题编制的题源.在高三复习迎考阶段，很多时候，在编制模拟试题或高考题时，会通过对教材中问题的适当拓展或延伸，改变题目的原有呈现形式，实现问题的推陈出新.这种“源于课本又高于课本”的考题，可以引导学生立足教材，强化“三基”的落实.对学生而言，这些问题看上去很熟悉，但与教材问题又有区别，解决问题的方法却是类似的，迁移了教材中解决问题的基本思想和方法.对教师而言，编制题目的过程体现了研究性学习的过程，体现了由特殊到一般，由封闭到开放的过程，同时也是提高教师命题能力的过程．近期，笔者参与命制了一套高三模拟试卷，现将该试卷中第14题命制的方式与过程以及命题后的反思展现出来，供同仁参考，不当之处敬请批评指正.

一、考题呈现

1.考题及其分析

若实数a、b、c、d满足 （b+a2-3lna）2+（c-d+2）2=0，则（a-c）2+（b-d）2的最小值为______.

分析：（a-c）2+（b-d）2表示点（a，b）与点（c，d）之间距离的平方.

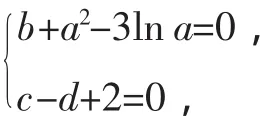
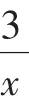
图1

2.考后反响

这道试题作为填空题的最后一题，其难度系数为0.32，有一定的区分度.考试结束后与部分学生和教师的交流过程中，普遍反映本题具有新意，与高考试题接轨，较好的考查了学生运用数学知识分析问题和解决问题的能力.

二、命制历程

1.题源

此题源于苏教版高中数学选修1-1第69页练习题的第3题：

选题缘由：接受任务时，命题组要求笔者出两道导数试题，其中一道填空题，一道解答题.由于导数是高考的必考内容，主要内容有导数的几何意义、单调区间、极值、最值等.为了全面考查导数知识，笔者决定在填空题中考查导数的几何意义.

2.试题的演变过程

鉴于考查目标，该题在原创之初如下：

命制感想：这样命制主要是保持了在原来考查导数的意图，同时还考查了学生转化的思想.但是感觉上没有灵气，缺乏高考的味道.经过再三思考，笔者做了如下调整：

雏形2：已知直线l：y=x+2与曲线C：y=-x2+3lnx，则曲线C上任意一点到直线l的最短距离为______.

命制感想：在整个组卷过程中，由于填空题中缺少一道把关题，因此命题组让笔者将这道试题再进行加工.为了增加这道题的难度，笔者试图增加题目的新意.于是笔者考虑将题目中的直线方程隐去，于是做了如下的修改：

雏形3：已知a∈R，若实数x，y满足y=-x2+3lnx，则（ax）2+（a+2-y）2的最小值是______.

命制感想：本题将原来的直线上任意一点到曲线距离、两点间的距离公式表示出来，即为点P（a，a+2）到点Q（x，y）之间距离平方的最小值.而P（a，a+2）、Q（x，y）分别在直线l：y=x+2和曲线C：y=-x2+3lnx上，问题的实质就是雏形2.在此基础上，笔者想能不能不直接给出曲线的方程呢？于是做出如下的调整：

雏形4：已知a∈R，b>0，则（a-b）2+（a+2+b2-3lnb）2的最小值为______.

命制感想：在命制完雏形4后，笔者感觉求解的式子过于烦琐，决定将待求的式子变简单点，将直线和曲线的条件放到条件中去，于是就得到如下的考题.

考题：若实数a、b、c、d满足（b+a2-3lna）2+（c-d+2）2=0，则（a-c）2+（b-d）2的最小值为______.

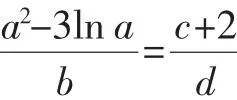
三、命题后的感想

教材凝聚了专家们的心智，教材中的例、习题都具有很强的基础性、典型性与示范性，它是教师教学的基础和根本，也是命题者的立足点.因此无论是高考还是模拟考试，在试题的命制过程中，都会考虑选用教材中典型的例、习题，作为测试内容进行考查.引导教师重视教材，扎扎实实地用好教材，引导学生重视课本，摆脱题海，切实打好基础.

加强教材例、习题的改编，能够引导学生重视教材.回归教材，能够使学生在清晰双基的基础上牢固掌握常见的数学方法，能够使学生在深刻理解教材知识的同时更有效地形成知识网络体系，还能够让学生有本可依，夯实基础，培养学习数学的自信心.

对于我们教师尤其是青年教师而言，通过改编试题和原创新题，可以让我们站得更高，看得更远；可以更方便地看出某类问题的实质所在；可以让我们在习题教学中更熟练地进行引申、延拓与变式，提高学生的应试能力；可以让我们在课堂教学中更加突出重点，注重方法，构建体系；原创更接近于高考的高质量试题，能更科学合理地检测出学生的学习状况与水平.

罗增儒教授说：“以能力立意命题，利于题型设计，易形成综合自然、新颖脱俗的试题.”总之，命制试题具有很深的学问.作为一线教师，我们必须要加强学习与研究，学习命题专家的命题技巧和技术，研究高考试题，研究教材，从中捕捉试题命制的素材，寻找灵感.

1.宋志永，陈云平.高中数学试题命制的一些思考［J］.中学数学教学参考（上旬），2012（4）.

2.王弟成.从模拟试题的解答，看教材使用的缺失［J］.中学数学教学参考（上旬），2011（12）.

3.沈新权，叶鹏.一道高考试题的背景及启示［J］.中国数学教育（高中版），2009（12）.