解题教学——想说爱你不容易
2013-07-25浙江省杭州市余杭高级中学曹凤山特级教师
☉浙江省杭州市余杭高级中学 曹凤山(特级教师)
笔者曾从学生“学”的角度,对数学解题的感受、认识等做过专题调查,调查报告《数学解题——想说爱你不容易——关于高中生数学解题的调查分析》发表于《中学数学教学参考》2005年第5期,后被中国人大《高中数学教与学》(原《中学数学教与学》)转载、被知网等收录,被不少同行参考、引用.本文换一个角度,从教师“教”的角度看,解题教学——想说爱你不容易.
“中学数学课程的主要目的之一是发展学生的解题能力”(波利亚),从现实需要看,解题教学的重要性毋须赘言.对于解题教学,虽有众多大家、名师诸多成功的实践与经典研究,但如何搞好解题教学仍然没有公式可循.一千个读者就有一千个哈姆雷特!一千个数学老师就有一千个解题教学的模式.
这里简录以解题教学为主的一节课,通过具体的案例和课堂教学环节,就解题教学中一些问题谈谈自己的思考与实践,以作引玉之砖.为便于表达对解题教学的一些认识,分成几个段落.
例题 (2012年浙江高考理科第17题)设a∈R,若x>0时,均有[(a-1)x-1](x2-ax-1)≥0,则a=_____.
一、选好题才有好效果
课堂例题就像磨刀石,只有好的磨刀石才能更快、更好地磨出锋利的刀刃.本文简录的是高三第一轮复习接近尾声的一节课,笔者以“三个二次”为核心,选择了两道2012年的高考题(浙江省理科第17题、北京理科第14题),其中第一题学生充分参与,老师详尽分析,第二题做课上反馈演练.不同教学阶段有不同的选题考虑,这里主要考虑了以下几个方面:
1.体现中学数学的核心知识,重心在思维.不在细枝末节上做文章,解题过程中突出知识的系统性、网络化、组织良好,突出提升思维能力的主题.
2.具有一定挑战性.试题新颖,两题都没有套路,解题过程蕴含着丰富的数学思想方法,而思想方法是知识转化为能力的桥梁,是高三复习过程中提升学生思维能力的必选项、着力点.
3.适合的就是最好的.适合学生的知识储备,适合学生的解题基础,适合学生的解题需要,题不在难,有意则灵.
4.以质取胜,体现通性通法.题不在多,有法则行,不追求一节课做题的数量,以高质量的试题实现“一题多解”、“多题一解”.法不在巧,变化则灵,凸显通性通法的重要作用,体现思维的高度参与.
5.完整体现解题的全过程,有效检验、提升学生的解题技能.学生学有所思、所悟,解透一题通解一类,对解题有更深的理解,对解题程序有更熟练的操作,特别是强化学生比较薄弱的方面,如审题、目标意识以及反思能力.
二、练熟解题程序,体验解题成功与失败历程
解题教学一定要有学生充分参与的过程,思路的产生不能玩“魔术”,要让学生体验.课堂生成与预设要相辅相成,要结合具体情境,通过适时的有针对性的启发、引导,适度的归纳、概括,帮助学生体验“审题——制订计划——实施——反思”的过程;落实学生先行,教师断后的教学模式,引导、调动学生的“正能量”参与解题,充分暴露、展示不同层次的思维模式、不同的思维过程,引导学生对解题的关键点、基本的数学思想方法的运用等做必要的归纳、反思,让学生体验审题对思路的决定作用,反思对模式积累的催化作用,注重由特殊案例提升到解题经验,改变解题教学“掐头、去尾、烧中段”的做法,改良为“虎头、豹尾、将军肚”的解题教学模式.
三、渗透共性的引导,启发问题个性、解法的形成发现
出示题目,学生自己读题(不干扰学生自己读题,不帮助学生读题.本题题干相对短小,学生用时不多).适时给出提示语,给学生做出反应、思考的时间.
师:这是什么问题?求什么?你能猜测到结果是什么形式吗?(目的:引导学生确定问题范畴,调动相关知识,强调目标意识、问题意识,进入问题情境)
生众:三次不等式,也有学生说“三个二次”,求参数;结果应该是一个(或者两个)常数.
师:用你的语言如何具体表述这个问题?你能联想到什么?有现成的方法吗?(目的:不仅强调审题的重要性,还要给出审题可以操作的方法.心理学研究表明,问题的表述对怎样解决问题有极大的影响.对审题跟进提醒,引导学生从文字、符号、图形等多角度审题,通过观察、对比、分析、判断,联想、调动所学知识,引导学生深入理解问题情境,对解题过程做出合理的预测,初步酝酿、设计从已知到目标的可能途径,诱导好“念头”的出现)
学生自己独立思考、探究,动手解题.巡视发现,因为是上一年的高考试题,有学生已经知道答案,但是,详细的解题方法、策略,深层次的思考还没有,解题方法不完整,还有部分学生找不到思路.
生1:我是根据实数运算的符号法则,降次,转化为一个一次、一个二次不等式,分以下两种情况:
师:生1同学注意到了关系式的符号,运用转化思想,把高次化低次、不等式转化成不等式组,再通过分离参数转化为求最值的问题,思路很流畅,可是解不出,问题出在哪儿呢?(审题表面化,考虑了问题的转化,模仿套路的痕迹比较明显,但是,对题目理解上出现偏差)
回到原点,再次读题,同学们对条件的形式、含义和生1同学的理解一致吗?(目的:引导学生再次审题,从条件的形式、代数意义、几何意义等方面读题,养成“慢审、快做”的习惯,优秀的解题者一半时间审题,一半时间做题,但有些学生可能“下笔千言,离题万里”.以上提示语问法不同、角度各异,但基本上都指向审题、启发解题思路)
生2:生1的理解不对.x>0时均有[(a-1)x-1](x2-ax-1)≥0,意思不一定是x>0时两个因式的值一直是正数或者是负数,只要两个因式同号.下面求解还没有写好.
师:对关系式的理解不一样,哪个是正确的?
全体:后一个!
师:对,后一个,注意关键词,若x>0时均有……,读对题是解对题的必要条件!解给出的问题而不是你认为的问题!不然肯定是“出师未捷身先死”啊!审题,就要让试题自己讲出“真实的情况”,继续!
生3:我没有看成两个因式乘积,我理解的是函数值符号问题,就是两个函数在区间(0,+∞)的每一点上函数值符号一致,这样必须有相同的零点.
师:打断一下,怎么出现的函数?不是不等式问题吗?(让思维过程看得见,充分暴露思维过程是学生学会思维,领悟数学思维的必然途径,特别是在一个转折点、关键点上)
生2:因为……因为……每个不等式都对应一个函数,不是可以转化吗?
师:很好,从不同的角度去推敲!不等式转化为函数问题,继续!
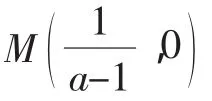
师:好!分解问题、数形结合是重要的解题思想,从不同角度理解条件是审题的重要形式、解题的突破口之一,也是找到“好念头”的捷径.
答案出来了,有学生表示还可以优化.
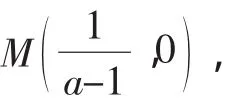
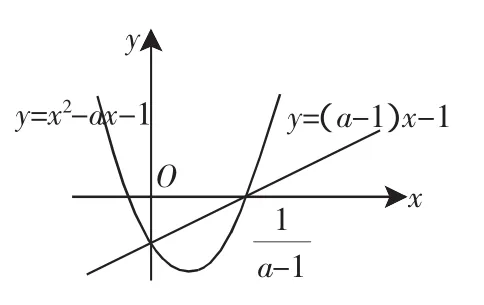
图1
教室内一片赞赏之声!
师:很好!问题的求解要像生2同学一样力求完善、直观,函数、方程、不等式联动,同时充分发挥了图形的优势,数形结合,分类讨论,让我们看到了数学思想方法的威力!

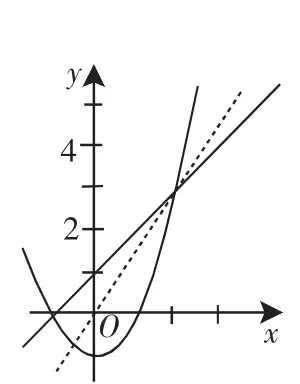
图2
师:很好,改变条件的形式,换个角度理解问题,避开了分类讨论.
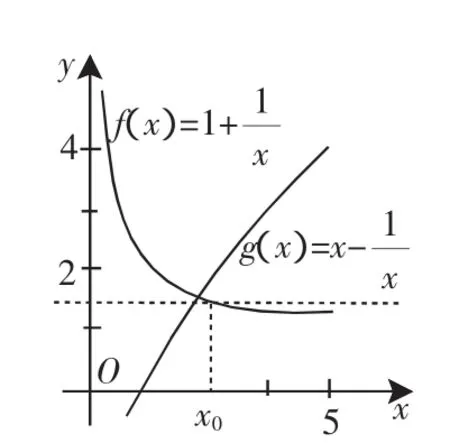
图3

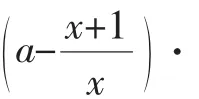
生5:老师,还可以再更简洁,只要再深入挖掘“个性”!
同学们的兴趣再次被激发,怎么再挖掘“个性”呢?
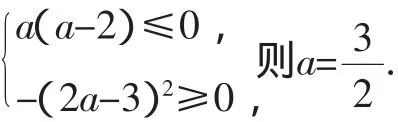
教室内一片掌声!
不过,有学生提出,保证f(1)≥0,f(2)≥0就能保证x>0时均有f(x)≥0吗?逻辑上明显有缺陷!
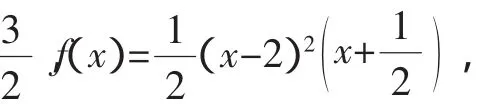
师:好,根据题型特征我们可以选择“个性化”的解题方法,思维灵活,体现了特殊性存在于一般性之中的哲学思想,解客观题不妨试试特殊值法,当然也要注意逻辑的严密性.

不过也有同学提出为什么恰好取x=2呢?
生6:开始老师不就是让我们猜测结果是什么形式吗?因为结果是求a的值,只有一个未知数,只要建立一个方程就可以了.
师:真有才!充分考虑目标的意义,对解题的方向会起到很好的启发作用,不能仅仅把目标当成未知数,它也是已知条件之一,是试题的“个性”之一.当然,为什么只取到2呢,要靠一点运气,不过,我们试验一般会取比较特殊的数,比如0,1,2等,再说了,我们是天之骄子一定会有好运气的,只要想得到,一定做得到!
我们发现,只要换个角度问题就可能得到解决,往往就是没有找到合适的角度.再次读这道题,a=1时显然不成立,它明显的特征是一个三次不等式,或者说三次函数问题,我们在学习导数内容时反复接触过三次函数以及它的图像、性质,能不能直接通过三次函数的视角求解呢?我们猜想三次函数图像会有什么特点?
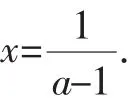
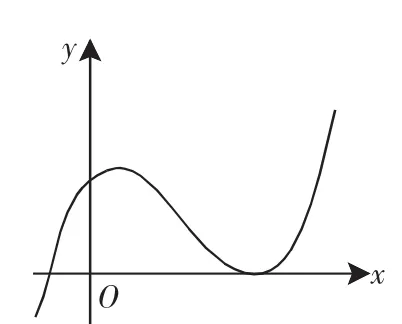
图4
四、适时引导反思、归纳,让学生积累个体成功经验
师:相当漂亮!对问题理解的透彻,解起来就得心应手!上面已经给出了不少好的解法,同学们也许还有其他想法,时间关系,暂告一段落,课下继续探讨!反思一下我们这道题的求解历程,从不懂到懂,从不会到会,从复杂到简单,我们经历了什么?对我们以后解题有什么借鉴意义?(引导学生做好解题反思,而不仅仅是找到答案,这也是解题与解题教学不同之处.解题关心结果,而解题教学关心解题的全过程,只要反思审题操作性的方法、解题突破口的发现、解法优劣及原因等)
学生七嘴八舌:审题、从不同角度看条件、改变条件的结构形式、画个图,把待求纳入已知考虑、找到它的“个性”、数形结合、转化与化归、分类讨论等.
师:同学们的总结综合起来就很全面了!我们通过这道题的求解,再次体验到,知识要熟练、组织良好,无知便无能;审题要全面、深入,注意对已知条件(包括题型、待求、待证)从不同角度、不同形式的理解,充分把握其“个性”;改变问题的形式、意义、结构就可能意味着一种解法的出现,要注意捕捉这时冒出的一些“好念头”;我们也会体验到,对于一些综合性、非常规问题,数学思想方法的自觉运用绝对功不可没,如数形结合、转化与化归、函数与方程、分类讨论等.基础题靠知识(扎实),中档题靠思想(灵活),高档题靠能力(素质).同时,从这道试题也可以看出高考试题的特点,知识与能力综合考查,体现了“多考一点想,少考一点算”的命题理念,需要我们在解题过程中真切体会.(小结不一定都要放在下课铃响之前,要适时、合理地给出概括,有背景、有案例,学生更容易理解,更容易纳入自己的经验范畴)
五、强化变式练习,巩固成果
下面再给出一道题,再一次体验如何成功解题!
练习 (2012年北京高考理科第14题)已知f(x)=m(x-2m)(x+m+3),g(x)=2x-2,若同时满足条件:①∀x∈R,f(x)<0或g(x)<0;②∃x∈(-∞,-4),f(x)g(x)<0,则m的取值范围是______.
选题的思考:本题和例题有异曲同工之妙,对学生熟练两个基本函数性质,熟练基本思想方法的运用,巩固上面例题中的一些思路、形成解题经验大有裨益.
学生经过思考,速度明显比例题加快.
生8:目标求m的取值范围,就是抛物线f(x)=m(x-2m)(x+m+3)开口方向与对应的根满足的条件(m=0明显不成立),“数”转化为“形”,等价于,对于任意的x,对应的点至少有一个在x轴下方,在(-∞,-4)上,有图像在x轴上方,有图像在x轴下方.
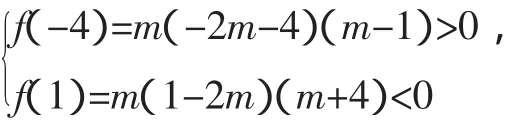
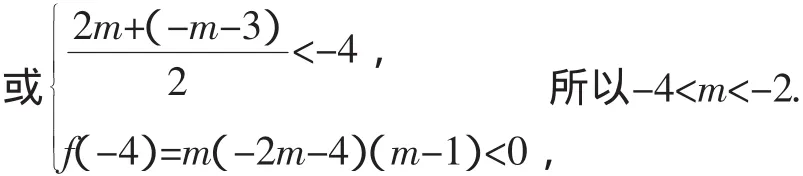
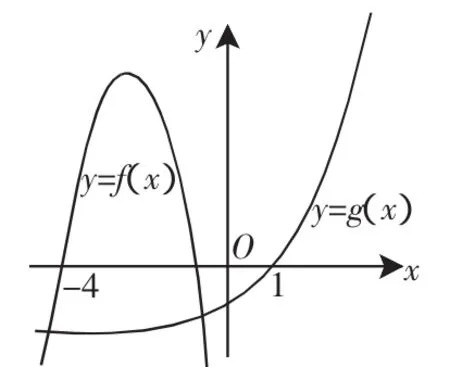
图5
师:太给力了!由于时间关系,对其他解法课下再继续探索.
通过这两道高考题,相信每个同学对解题都有自己的感悟,也会发现自己在哪些方面还需要加强,希望同学们再通过以下三道课下练习题认真反思、总结.
选择课下练习题的思考:解题是学会的,不是教会的,必须在游泳中学会游泳,特别是突出思维,体现思想方法运用的问题,学生必须有自己的体验,感悟,有操作程序,能设计已知到目标的合理途径,面对高考“活而不难,巧而不怪”的特点,必须在合适的情境下选择高质量、符合学生实际的问题.选题知识上有一定综合性,试题题目不追求绝对难度,主要是知识的综合应用、灵活应用;体现基本数学思想方法的运用,这是学生解题的一块“短板”,当知识的积累达到一定程度,学生解题能力提高的加速剂就是思想方法,它是知识转化为能力的桥梁,特别是重要的数学思想如转化与化归、数形结合、函数与方程、分类讨论等,数学思想方法的运用到复习阶段必须给学生明确揭示,让学生在运用中体验、感悟.
1.(2012年北京高考文第14题)已知f(x)=m(x-2m)·(x+m+3),g(x)=2x-2.若∀x∈R,f(x)<0或g(x)<0,则m的取值范围是_________.
2.(2008年江西高考理科第12题改编)已知函数f(x)=2mx2-2(4-m)x+1,g(x)=mx,若对于任一实数x,f(x)与g(x)至少有一个为正数,则实数m的取值范围是_______.
3.(2011年江苏高考第19题)已知a,b是实数,函数f(x)=x3+ax,g(x)=x2+bx,f′(x)和g′(x)是f(x)和g(x)的导函数.若f′(x)g′(x)≥0在区间I上恒成立,则称f(x)和g(x)在区间I上单调性一致.
(1)设a>0,若f(x)和g(x)在区间[-1,+∞)上的单调性一致,求实数b的取值范围;
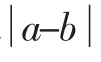
1.[美]波利亚,著.怎样解题[M].阎育苏,译.北京:科学出版社,1982.
2.罗增儒,著.中学数学解题的理论与实践[M].南宁:广西教育出版社,2012.
3.[英]S.Ian Robertson,著.问题解决心理学[M].张奇,等,译.北京:中国轻工业出版社,2004.
