欣赏圆锥曲线的和谐美——两道高考题的解法及结论推广

☉南京师范大学第二附属高级中学 朱 斌

（1）求直线A1P与A2Q交点的轨迹E的方程式；（2）略.

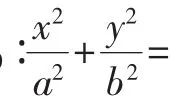
（1）求直线AA1与直线A2B的交点M的轨迹方程；

（2）略.

本文只讨论问题的第（1）问，通过探究与思考，欣赏其中的数学美.

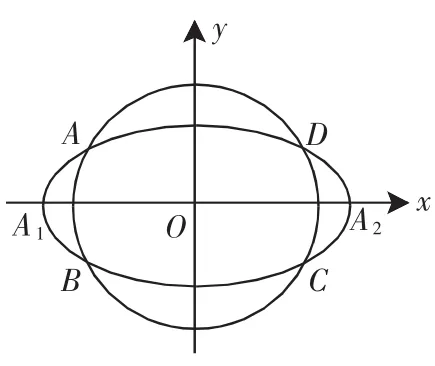
图1

粗一看，两个问题的条件并无多大关联，问题的问法却神似.事实上，题目2中的点A、B与题目1中的点P、Q是等效的（关于x轴对称）.下面以题目2为例展开探究.

一、解法之美

一个数学问题可以从多种角度去思考，并且都能得到最终想要的结果，那么这个问题就是一个好问题.上述题目就是这样一类问题，下面给出几个不同思考角度的几种解法.

解法1：设A（x1，y1），B（x1，-y1），又知A1（-a，0），A2（a，0），则

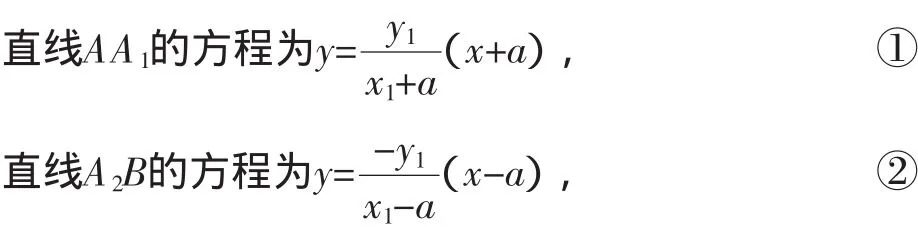
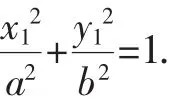
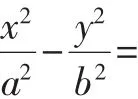
解法2：设A（x1，y1），B（x1，-y1），又知A1（-a，0），A2（a，0），则

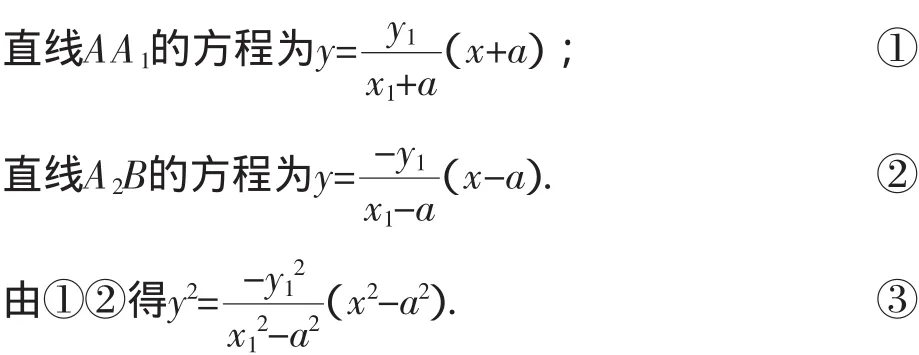
解法3：设A（x1，y1），B（x1，-y1），又知A1（-a，0），A2（a，0）.设A1A：y=k1（x+a），A2B：y=k2（x-a）.

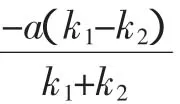
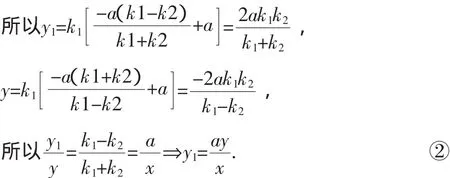
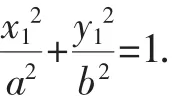
解法4：由已知直线AA1与直线A2B的交点M，因为A1、M、A三点共线，所以

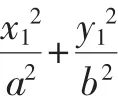
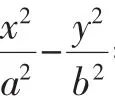
二、结构之美

说明：以上4种解法都可以证明，这里不再重复.

命题2的证明也都可以用上面的4种解法来解决，证明过程是类似的，限于篇幅，这里就不详述了.

上述题目1（2010年广东卷理20）就是该命题的特例，简解如下：

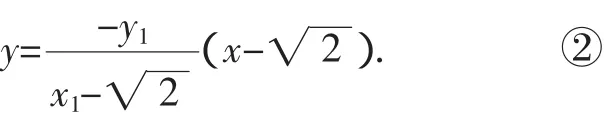
设点M（x，y）是A1P与A2Q的交点，由①×②得

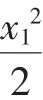
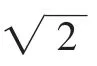
同理轨迹E也不经过点（0，-1）.

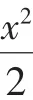
三、对称之美

由题目的左、右顶点分别为A1，A2知，A1和A2是关于y轴对称，而由点P（x1，y1），Q（x1，-y1）的坐标知，P和Q是关于x轴对称.若把这两个对称关系改变一下，即A1和A2是关于x轴对称，P和Q是关于y轴对称，又会出现什么样的结果呢？

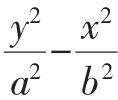
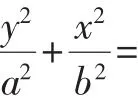
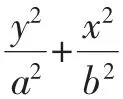
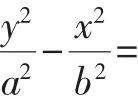
四、结束语

以上是在解题过程中，发现了高考中两道解析几何题的数学之美.数学美是数学的魅力之一，数学美是数学能吸引众多数学爱好者的原因之一.这种数学美，即使是在紧张的应试过程中，也能发现其中的美妙规律，也会获得美的感受.

因此，像这种蕴含丰富的数学美的题目，应该多出现在各大考试之中，让更多的人去欣赏数学之美，让更多的人去喜欢数学，让考试成为一种赏美的乐事.

1.易南轩．解题中的数学美［J］.西安：中学数学教学参考，1998（7）：32-34．

2.王林全．数学美的丰富蕴含［J］.北京：数学通报，2011（3）：48-51.