一个代数不等式与几个有趣的三角不等式

☉云南省漾濞县第一中学 秦庆雄 范花妹

本文将首先证明一个简单的代数不等式，然后由它可以推出一系列三角形中的优美不等式，其中包括著名的匹多（Pedoe）不等式的加强、费恩斯列尔（Finsler）-哈德维格尔（Hadwiger）不等式的加强等，以及其他一些有趣的不等式.

一、一个代数不等式及其证明

定理 设实数x′，y′，z′及x，y，z同时满足x′+y′+z′＞0，x+y+z>0，x′y′+y′z′+z′x′>0，xy+yz+zx>0，那么

当且仅当x′：x=y′：y=z′：z时（*）式中的等号成立.

证明：要证（*）式成立，只需证（x′+y′+z′）2（x+y+z）2≥（x′+y′+z′）（x+y+z）（x′x+y′y+z′z）+（x′+y′+z′）2（xy+yz+zx）+（x+y+z）2（x′y′+y′z′+z′x′）成立.

由均值不等式和柯西不等式，可得：

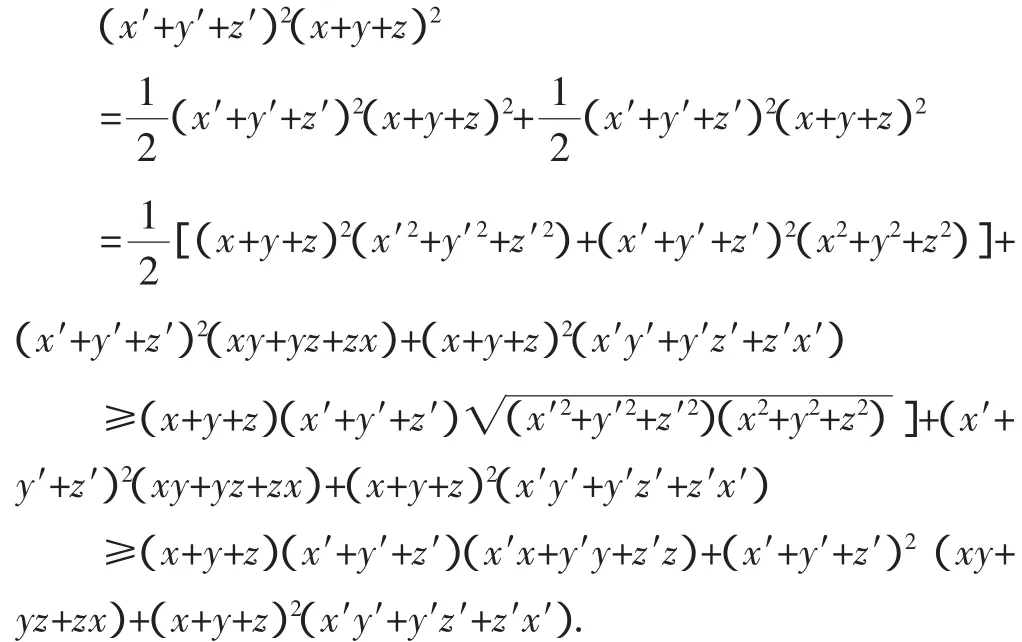
即（x′+y′+z′）2（x+y+z）2≥（x+y+z）（x′+y′+z′）（x′x+y′y+z′z）+（x′+y′+z′）2（xy+yz+zx）+（x+y+z）2（x′y′+y′z′+z′x′）成立，由均值不等式和柯西不等式取等号的条件知，当且仅当x′：x=y′：y=z′：z时（*）式等号成立，从而定理获证.

二、三角形中几个有趣的不等式

本文中，用a，b，c，S与a′，b′，c′，S′分别表示△ABC和△A′B′C′的边长及面积.

命题1 在△ABC和△A′B′C′中，有不等式：

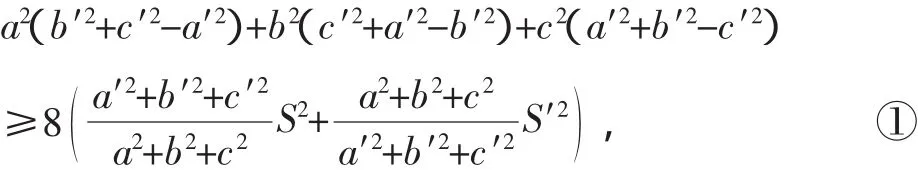
当且仅当△ABC∽△A′B′C′时，①式取等号.

据三角形面积的秦九韶公式，得：

同理，可得x′y′+y′z′+z′x′=16S2.

将以上各式代入（*）式，便得到①式.

说明：不等式①，由中国科学技术大学的彭家贵教授和常庚哲教授于1983年在文［1］中提出并证明，这里给出了另一种证明.

对①式的右边用均值不等式，便可得

推论1 在△ABC和△A′B′C′中，有不等式

a2（b′2+c′2-a′2）+b2（c′2+a′2-b′2）+c2（a′2+b′2-c′2）≥16SS′，当且仅当△ABC∽△A′B′C′时等号成立.

上式即为著名的匹多（Pedoe）不等式，可见①式是比匹多（Pedoe）不等式更精细的不等式.

由①式出发，我们可以推导出另外一些涉及两个三角形的不等式.

推论2 在△ABC和△A′B′C′中，有不等式：

当且仅当△ABC与△A′B′C′均为正三角形时，②式取等号.

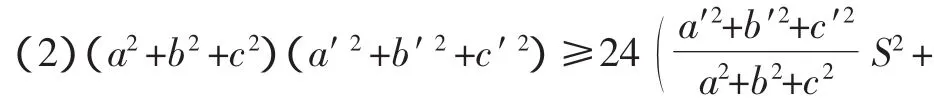
当且仅当△ABC与△A′B′C′均为正三角形时，③式取等号.

简证：我们对△ABC与△B′C′A′、△ABC与△C′A′B′两次使用①式，可得

将④与⑤两式两边分别相加后同时除以2，便得

当且仅当△ABC与△A′B′C′均为正三角形时，②式取等号.

将①、④与⑤三式两边分别相加，便得：

当且仅当△ABC与△A′B′C′均为正三角形时，③式取等号.

命题2 在△ABC和△A′B′C′中，有不等式

当且仅当△ABC∽△A′B′C′时，⑥式取等号.

将以上各式代人（*）式，便得到⑥式.

说明：不等式⑥，由宋庆老师（现任教于江西南昌大学附属中学）于1989年在文［2］中提出并证明，这里给出了另一种证明.

对⑥式的右边用一下均值不等式，便可得

推论3 在△ABC和△A′B′C′中，有不等式：当且仅当△ABC与△A′B′C′为正三角形时等号成立.

上式由重庆市第二十三中学高灵老师于1981年提出，并发表于美国《Mathematics Magazine》第55卷（1982）第5期299页上的问题1156，可见⑥式是比高灵不等式更精细一些的不等式.

由⑥式出发，我们可以推导出另外一些涉及两个三角形的不等式.

推论4 在△ABC和△A′B′C′中，有不等式：

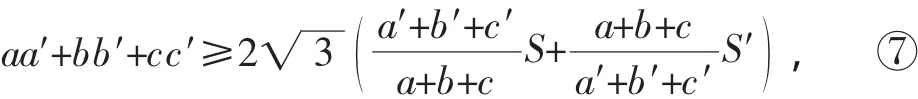
当且仅当△ABC与△A′B′C′均为正三角形时，⑦式取等号.

当且仅当△ABC与△A′B′C′均为正三角形时，⑧式取等号.

简证： 我们对△ABC与△B′C′A′、△ABC与△C′A′B′两次使用⑥式，可得：

将⑨与⑩两式两边分别相加后同时除以2，便得：

命题3 对任意△ABC和△A′B′C′中，有不等式：

当且仅当△ABC∽△A′B′C′时式取等号.

将以上各式代人（*）式，便得到式.

推论5 对任意△ABC和△A′B′C′中，有不等式：

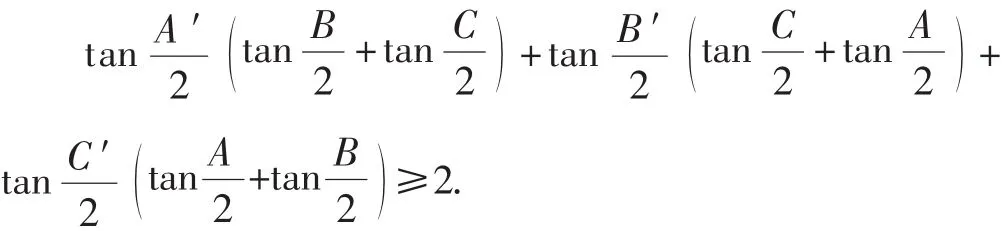
当且仅当△ABC∽△A′B′C′时，上式取等号.

说明：上式即为陕西省咸阳师范学院安振平老师于2012年在文［3］中提出的定理1，可见式是比上式更精细一些的不等式.

命题4 对任意△ABC和△A′B′C′中，有不等式：

当且仅当△ABC∽△A′B′C′时式取等号.

简证:在（*）式中，令x=cotA′，y=cotB′，z=cotC′，x′=cotA，y′=cotB，z′=cotC.

在△ABC和△A′B′C′中，易得：

将以上各式代人（*）式，便得到式.

推论6 对任意△ABC和△A′B′C′中，有不等式：

当且仅当△ABC∽△A′B′C′时，上式取等号.

说明：上式即为陕西省咸阳师范学院安振平老师于2012年在文［3］中提出的定理2，可见式是比上式更精细一些的不等式.

命题5 在△ABC和△A′B′C′中，有不等式：

则x′+y′+z′=a2+b2+c2，x+y+z=2（a′b′+b′c′+c′a′）-（a′2+b′2+c′2）.

据三角形面积的秦九韶公式，得：

据三角形面积的海伦公式，得：

即xy+yz+zx=16S′2.

将以上各式代人（*）式，便得到式.

对上式经过恒等变形，可以得到：

推论7 在△A′B′C′中，有不等式：

当且仅当△A′B′C′为正三角形时等号成立.

推论8 在△A′B′C′中，有不等式：

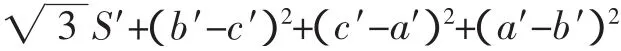
a′2+b′2+c′2≥2，当且仅当△A′B′C′为正三角形时等号成立.

上式即为著名的费恩斯列尔（Finsler）-哈德维格尔（Hadwiger）不等式，可见式是比费恩斯列尔（Finsler）-

哈德维格尔（Hadwiger）不等式更精细一些的不等式.

命题6 在△ABC和△A′B′C′中，有不等式：

当且仅当△ABC∽△A′B′C′时式取等号.

z=（a′+c′-b′）（b′+c′-a′），

则x′+y′+z′=2（ab+bc+ca）-（a2+b2+c2），x+y+z=2（a′b′+b′c′+c′a′）-（a′2+b′2+c′2）.

据三角形面积的海伦公式，得：

将以上各式代人（*）式，便得到式.

推论9 在△ABC和△A′B′C′中，有不等式：

当且仅当△ABC∽△A′B′C′时式取等号.

上式由陕西省咸阳师范学院安振平老师在《数学通讯》1987年第6期上提出，可见式是比安振平不等式更精细一些的不等式.

据三角形面积的秦九韶公式，得：

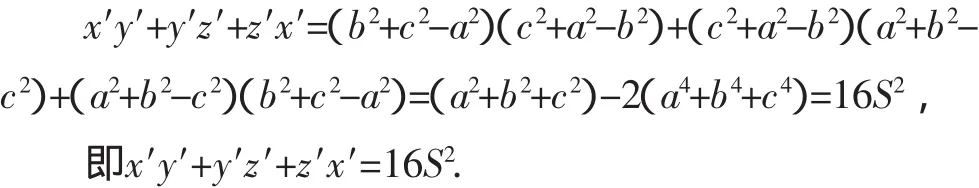
将以上各式代人（*）式，便得到式.

推论10 设实数x，y，z同时满足x+y+z＞0，xy+yz+zx＞0，在△ABC中，有不等式：

问题：在△ABC中，有不等式：

1.彭家贵，常庚哲.再谈匹多不等式.初等数学论丛（第6辑）［M］.上海教育出版社，1983（7）：17-25.

2.宋庆.一个三角不等式的加强［J］.湖南数学通讯，1989（4）：26-37.

3.安振平.涉及两个三角形角元的一个不等式［J］.中学数学教学参考，2012（9）：28-29.

4.刘保乾.一组仅含三角形边长的不等式.第三届全国初等数学研究学术交流论文集 （福州）［M］.1996（8）：559-571.

5.张小明.一个猜想不等式的证明：不等式研究（第一辑）［M］.拉萨：西藏人民出版社，2000（6）：271-274.