双曲线不等式及其应用

☉广东省佛山市高明区第一中学 林建雯

我们知道双曲线有很多的性质及应用，其实双曲线的方程与不等式之间也有联系，这种联系对发现问题、解决问题、研究问题带来了很大的方便.下面笔者试着探索和研究这方面的内容，以供参考.

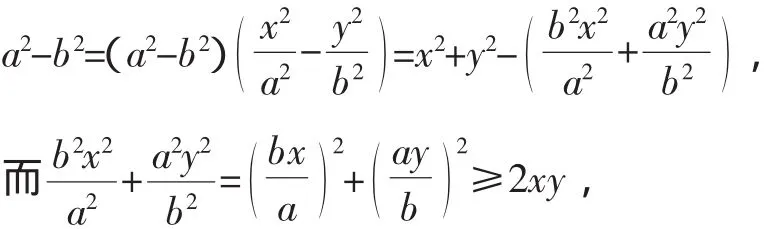
因此a2-b2≤x2+y2-2xy=（x-y）2，

即a2-b2≤（x-y）2.

由不等式①我们很容易获得下面两个有趣的推论：

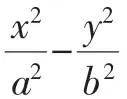
又因为a2-b2≥0，λ0≥λ，

所以λ（a2-b2）≤（x-y）2.

上述3个不等式的应用非常广泛，特别是用来求二元函数最值或值域问题时，显得更加简洁和方便.

一、求满足整式方程未知数的代数式的最值或范围

例1 已知x，y满足x2-y2-2x-4y=0，求x-2y的范围.

由推论1得

解得x-2y≤2或x-2y≥8.

所以x-2y的取值范围为（-∞，2］∪［8，+∞）.

例2 已知a，b∈R，且2a+b-2=0，求（a-2）2-（b-3）2的最大值.

由推论1得

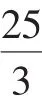
二、求满足三元一次方程及三元二次方程的未知数的最值

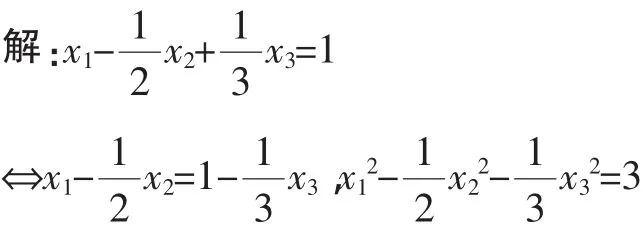
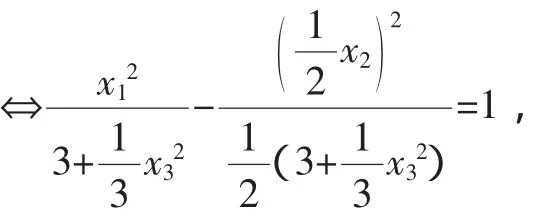
三、求满足整式方程未知数的分式的最值或范围

由推论1得（3k2-3）≤［（k+kx）-y）］2=k2，

四、求满足不等式的未知数的最值

例7 如果实数x，y满足不等式（x+1）2-y2≥3，求2x-y的取值范围.

解：由已知不等式（x+1）2-y2≥3可得

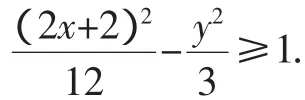
由推论2得（12-3）≤［（2x+2）-y）］2=（2x-y+2）2，即9≤（2x-y+2）2，-5≤2x-y≤1，从而2x-y的最大值为1，最小值为-5.

五、求无理函数的值域

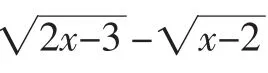
解：由2x-3≥0且x-2≥0得x≥2.

六、求满足分式方程未知数的代数式的最值