借“画板”之手，破中考压轴——对一道中考填空压轴题的思考

☉广东省佛山市顺德区龙江龙山初级中学 邓继雄

以函数图像为背景，根据函数图像的性质，结合几何图形的基本性质进行相关的计算或证明，是中考数学的热门题目.现提供一道中考填空压轴题，并提出个人的见解，与同行交流探讨，以期在今后的解题教学中有所帮助.

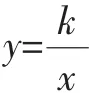
（1）当点O′与点A重合时，点P的坐标是______；

（2）设P（t，0），当O′B′与双曲线有交点时，t的取值范围是________.

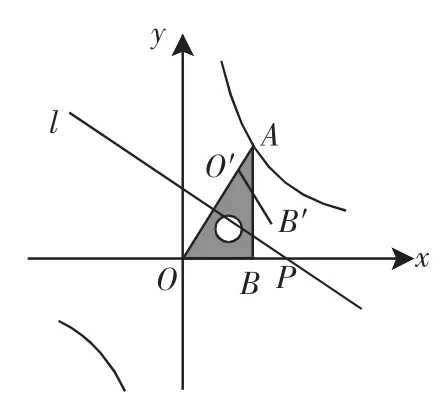
图1

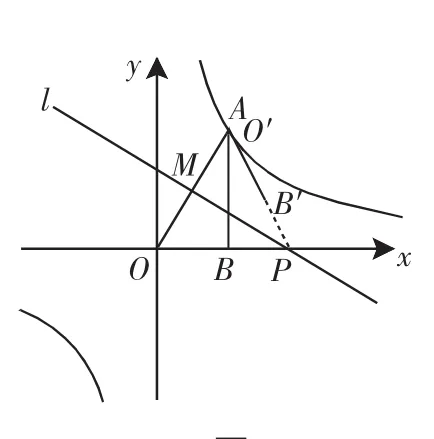
图2

分析：由题意可知，直线l为题中轴对称变换过程中的对称轴，且PM⊥直线OA.

由∠AOB=60°，知：

∠OPM=30°.

由轴对称变换可知：

∠O′PM=∠OPM=30°.

所以∠OPO′=60°.

所以△OPO′是等边三角形（如图2）.

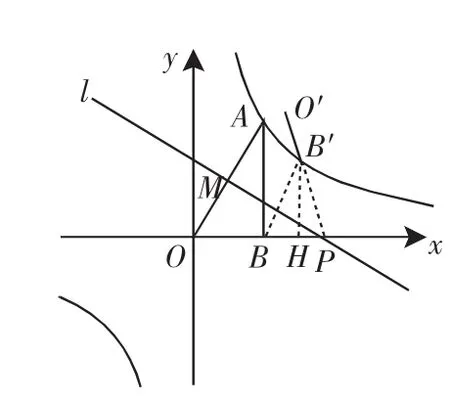
图3

如果连接BB′，则有△BPB′也是等边三角形（如图3）.

根据以上关系，我们就可以解决该填空题了.

解答：（1）当点O′与点A重合时，如图2，

因为B点的坐标是（2，0），即OB=2，而∠AOB=60°，所以OA=2OB=4.

因为△OAP是等边三角形（具体过程不再重复），

所以OP=OA=4，即点P的坐标是（4，0）.

说明：第（1）题因为位置比较特殊，点O′与点A重合，图形非常直观，关系比较明显，答案容易求出，属于常规题.

（2）容易求得点A的坐标是（2，2），而双曲线经过点A，可以求出反比例函数的解析式为①；由图2中△OPO′是等边三角形可知，O′、B′所在的直线经过点P，且与x轴所成的角等于60°，于是设直线O′B′的解析式是y=－x+b，把点P的坐标（t，0）代入求出直线O′B′的解析式是y=－x+t②.如果仅考虑直线O′B′与双曲线有交点，则由①、②组成方程组，整理得x2－tx+4=0，方程有解必须满足Δ≥0，即t2－16≥0，解得t≥4或t≤－4.

考虑本题是线段O′B′与双曲线有交点的相关问题.借助几何画板操作观察，我们可以发现，O′B′与双曲线的交点在第一象限内，即图2中当点O′与点A重合时，对应t取到最小值4；图3中当点B′刚好落在双曲线上时，对应t取到最大值.此时过点B′作B′H⊥x轴于点H，在等边△BPB′中，设BH=a，则B′H=a.于是点B′的坐标为（a+2，a），代入双曲线的解析式得方程a（a+2）=4，解得a=－1±，这里取a=－1+，负值舍去，所以BP=2BH=2a=－2+2，于是OP=OB+BP=2+（－2+2）=2，此时取得t的最大值为2.

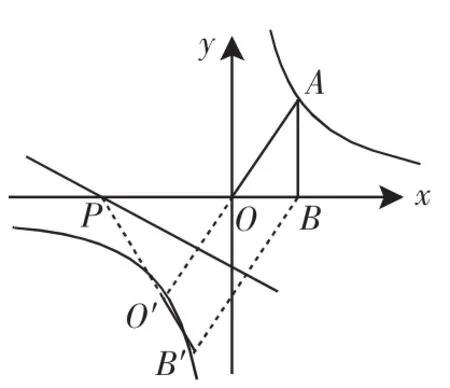
图4

结论：交点在第一象限内时，t的取值范围是4≤t≤2.当O′B′与双曲线的交点在第三象限时，如图4，点O′在双曲线上时，对应t取到最小值；点B′在双曲线上，对应t取到最大值.具体数值可以根据双曲线关于原点中心对称，结合本题的轴对称的性质得到t的最小值为－2，最大值为－4.当然也可以类似于第一象限内的求法，有兴趣的读者不妨试试.总之，交点在第三象限内t的取值范围是－2≤t≤－4.

综上所述，当O′B′与双曲线有交点时，t的取值范围是4≤t≤2或－2≤t≤－4.

说明：第（2）题的解题思路比较复杂，同时又是一个动态问题，用到了分类讨论的思想，解题过程中应用了待定系数法求一次函数、反比例函数的解析式，同时考查对勾股定理、解二元一次方程组、解不等式、含30度角的直角三角形的性质、三角形的内角和定理、根的判别式等知识点的理解和掌握，能综合运用这些性质进行计算是解答此题的关键，此题是一个拔高的题目，有一定的难度.

思考：这是一道中考填空题的最后一题，显然有一定的难度，而对于填空题一般只是提供参考答案，无法得知解题的思路，通过百度文库搜索，可以查到该份试卷的解析版，读者可以从网上查阅，其中本题的参考答案中计算量相当大，计算难度较高，所列的直线O′B′的解析式相当复杂，关于判别式Δ≥0的不等式难度更大，如果能较好地结合几何图形的性质进行解题，将能大大减少计算，起到事半功倍的效果.本文所提供的解法，就能较好地体现解题的优越性，同时渗透数形结合这一重要的数学思想.