特殊值法应用八型

☉

目前，全国各地特别强调通性通法，这无疑是正确的，但在强调通性通法的同时，不应该忽视特性特法，通性通法与特性特法是对立统一的，是相互依存的，通性通法是相对于特性特法而言的，无特性特法则也无通性通法.故坚持特性特法的研究是有一定道理的.2012年高考天津卷文科第（4）题、辽宁卷理科第（11）题、全国大纲卷文科第（6）题等不少试题的求解都用到了取特殊值的方法，或者说用取特殊值的方法收效较好.

在解某些数学问题时，选择适当的量，赋以一些特殊值，再分别进行研究；或将一些特殊值带入给定的表达式，以解决给定的问题；或将一般问题特殊化，复杂问题简单化，发现规律，寻求结论，探索解决问题的途径，这种方法可称为特殊值法，下面我们分八种类型谈谈特殊值法的应用.

一、解选择题

例1 多项式（x+1）（x+2）…（x+n）（n≥2，n∈N）乘开整理后，xn-2项的系数为（ ）.

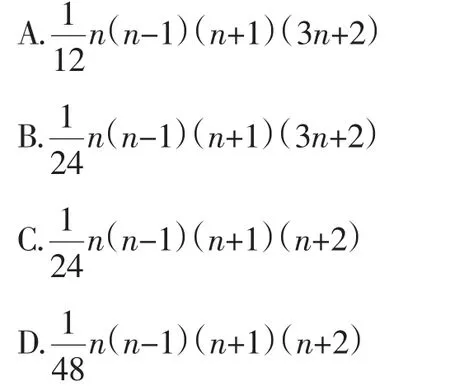
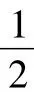
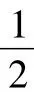
二、待定系数

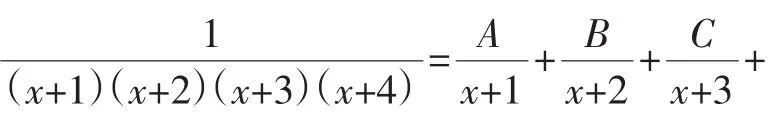
解：使原式成立的A、B、C、D也必使

A（x+2）（x+3）（x+4）+B（x+1）（x+3）（x+4）+C（x+1）（x+2）（x+4）+D（x+1）（x+2）（x+3）=1恒成立.

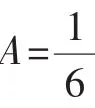
点评：去分母，将分式等式变成整式等式，其中四次进行多项式乘以多项式，再利用多项式恒等，解方程组也可求出A、B、C、D的值，但那样相当浩繁，苦不堪言.在这里，特殊值法清新自然、活泼可爱.

三、求代数式的值

例3 设（x2+x+1）1006=a0+a1x+a2x2+…+a2012x2012，求

log3［2（a0+a2+a4…+a2012）-1］的值.

解：令x=1有31006=a0+a1+a2+a3+…+a2012；

令x=-1有：1=a0-a1+a2-a3+…+a2012.

两式相加有：31006+1=2（a0+a2+a4+…+a2012），

所以log3［2（a0+a2+a4…+a2012）-1］=1006

点评：令x=1、令x=-1，这是在用特殊值法，但其实这就是这类问题求解的通性通法，这也说明特性特法有时就是通性通法，这时它们并不对立而是统一的.在这里，特殊值法探囊取物、妙手揭盖.

四、用于反证法

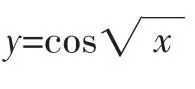
证明：函数定义域为非负实数集，假设y=cos是周期函数，则存在常数T≠0，使得定义域内的一切x都满足cos

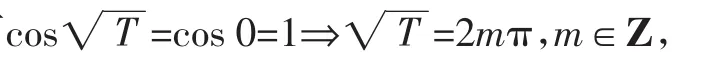
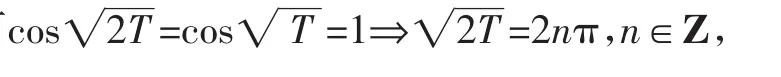
点评：否定性命题的证明，大多用反证法，假设原命题不成立之后，寻求矛盾是关键，本题妙取两个特殊值矛盾立现.在这里，特殊值法立竿见影、多姿多彩.

五、函数性质的证明

例5 已知整式函数y=f（x），对一切a、b∈R，等式f（ab）=f（a）+f（b）恒成立，求证：f（x）必有因式x2-x.

解：令a=b=0有f（0）=f（0）+f（0）⇒f（0）=0，所以f（x）必有因式x.

令a=b=1有f（1）=f（1）+f（1）⇒f（1）=0，所以f（x）必有因式x-1.

从而f（x）必有因式x（x-1），即x2-x.

点评：因为整式函数y=f（x）有因式x-m等价于f（m）=0，故本题只需证明f（0）=0、f（1）=0，令a=b=0，得f（0）=0，令a=b=1，得f（1）=0，问题立即得解.在这里，特殊值法赏心悦目，舒心爽快.

六、发现规律探求结论

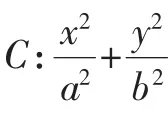
（Ⅰ）求椭圆C的标准方程；

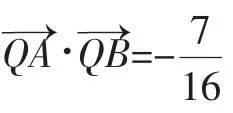
解：（Ⅰ）略，

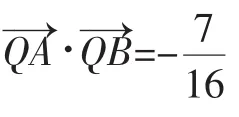
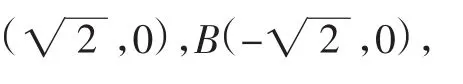
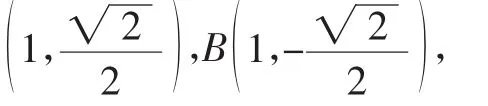
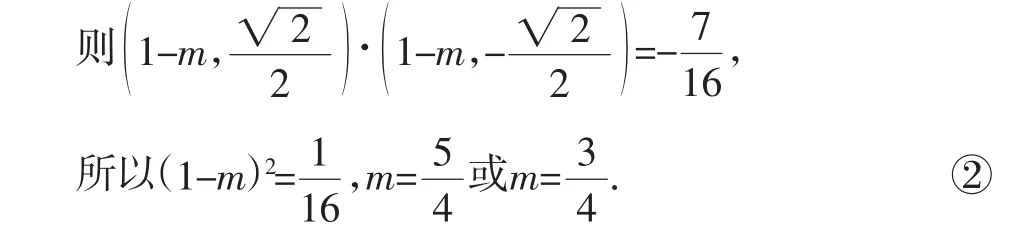
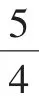
七、归纳猜测结论

例7 已知数列{an}，{bn}满足a1=1，b1=2，若an，bn，an+1成等差数列，

并且bn，an+1，bn+1成等比数列，求两数列的通项公式.

解：由已知有2bn=an+an+1，且1，又a1=1，b1=2，

计算得{an}前三项为：1，3，6，

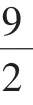
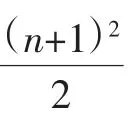
证明：（略）.

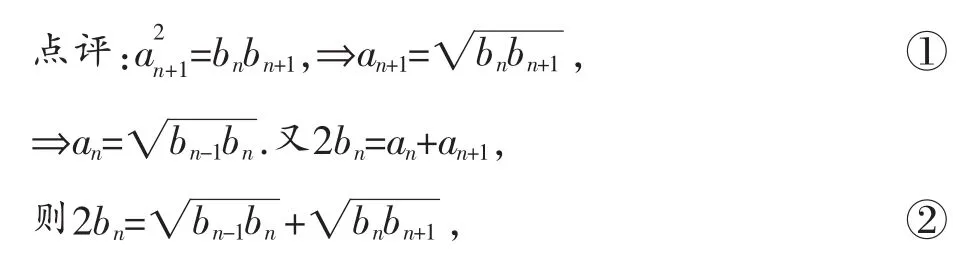
八、解决“恒成立”问题

例8 已知a，b，A，B∈R，f（θ）=1-acos θ-bsin θ-Acos 2θ-Bsin 2θ，

对于任意θ都有（fθ）≥0，求证a2+b2≤2，A2+B2≤1.

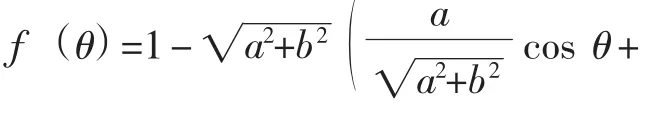
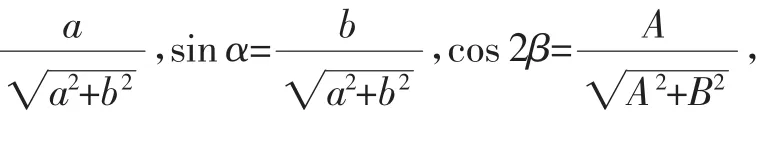
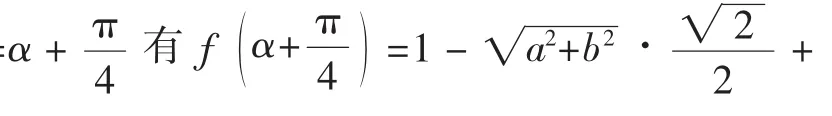
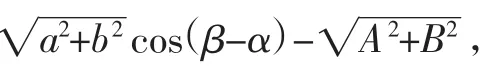
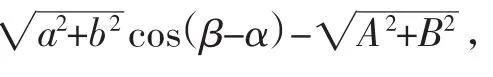
由已知有：f（β）≥0，f（π+β）≥0，

点评：利用辅助角化简原函数式，是比较明显的，因为结论中有平方，接下来直接证明所给两个不等式是颇有难度的，既然所给条件是一系列不等式，那就不妨先取几个已知不等式出来进行研究，这就是特殊值法.妙取四个特殊值，一切问题迎刃而解.至于如何取得理想的特殊值，那也有蛛丝马迹可寻，容下文分解.在这里，特殊值法另辟蹊径，奇兵奏凯.

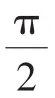
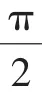
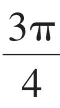
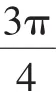
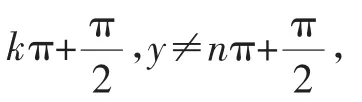
所以tan0+tana+tan0tana=b⇒b=tana.①

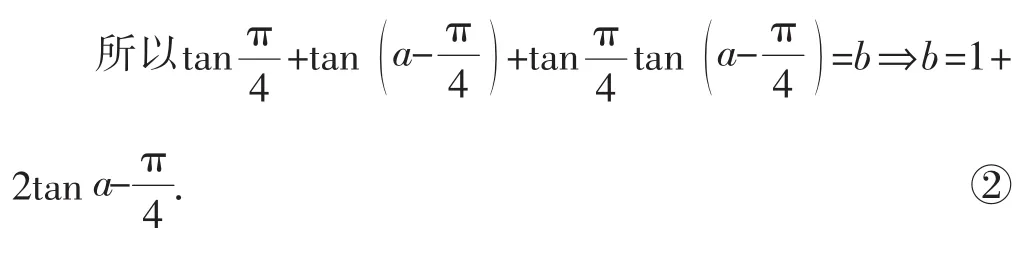
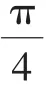
综上所述，特殊值法应用广泛，既能简洁迅速解选择题，待定系数，求代数式的值，求定点坐标，辅助反证法推出矛盾，又能发现规律寻求结论，也能别开生面的解决“恒成立”的等式、不等式等问题.