不等式有若干个整数解求参范围的解题策略

☉

对于不等式有解或者方程在给定范围有解问题是高中常见题型，由于平时训练得较多，对学生已不是难点.但近来各地的高三测试题的客观压轴题多次出现不等式或方程有若干个整数解求参数问题，学生感到对整数这个限制条件如何转化比较困难，得分率较低.因此本文选择部分代表性题目加以阐述.

例1 （连云港市2013届高三二模）关于x的不等式x2－ax+2a＜0的解集为A，若集合A中恰有两个整数，则实数a的取值范围是______.

法一：根据二次函数图像的特征求解

解：由题意知Δ=a2－8a＞0，得a＞8或a＜0.

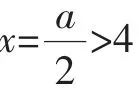
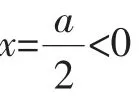
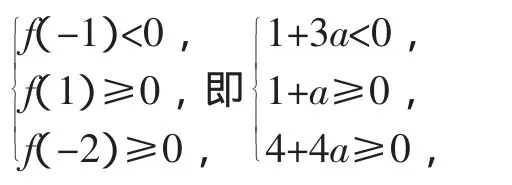
评注：由于题目所给的条件是以二次不等式的形式出现，因此可直接构造二次函数.但要挖掘出二次函数的隐含条件.如本题在a＞8前提下，由对称轴x＞4，f（4）＜0，且A中恰有两个整数，因此f（3）＜0不成立（否则由二次函数对称性，f（5）＜0，至少有三个整数满足不等式，不符合题意），即满足条件的整数只能为4与5，而得到相应条件.

法二：分离参数，构造新函数，根据新函数图像确定应该整数解

解：由x2－ax+2a＜0得x2＜a（x－2），若x－2=0，显然不成立；

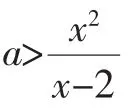
同理，当x－2＜0时，

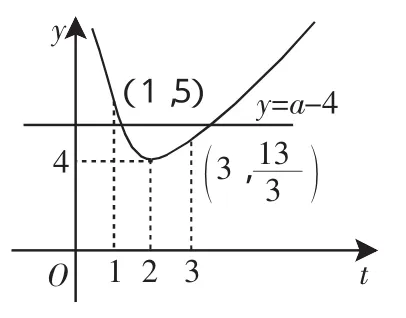
图1

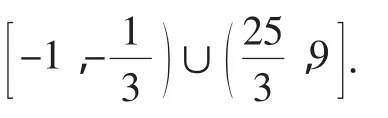
例2 （2009年天津文）若关于x的不等式（2x－1）2＜ax2的解集中整数恰有三个，则实数a的取值范围为______.

解法1：由（2x－1）2＜ax2得（4－a）x2－4x+1＜0，由题意知该不等式有解，

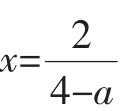
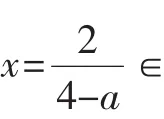
没有整数解满足不等式（4－a）x2－4x+1＜0.

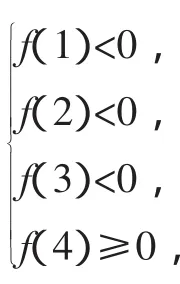
评注：本题构造出函数f（x）=（4-a）x2-4x+1后，无法确实f（x）＜0某一个具体对应的整数值，就必须尝试具体函数值与对称轴相对位置关系.此法的关键点是判断出f（1）＜0必然成立.

解法2：由（2x-1）2＜ax2得（4-a）x2-4x+1＜0，由题意知该不等式有解，

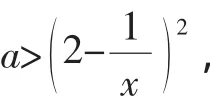
因为满足该不等式的整数解恰有三个，若x≤-1，则a＞4，不成立.

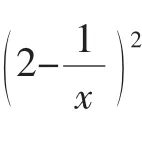
因此满足该不等式整数解恰有三个，则必为1，2，3，

总结：由上面的解法可以看出，二次不等式有有限个整数问题，常用方法有两种.一是构造二次函数，挖掘出某个特定的整数变量值满足要求后，结合二次函数图像，根据所得的特定整数解以及与对称轴位置关系，确定满足条件的所有解，写出条件；另一种方法是分离参数，构造新函数，根据新函数的图像或所具有的函数性质，确定整数应该是哪几个，从而得到参数的范围.对于这类问题一般不需要求出不等式的解集，除非有一根是常数.因此文［1］对例2的解法显然不够严谨的，且由于没有注意区间开闭，结果也是错误的.

例3 （2009年天津理）设0＜b＜1+a.若关于x的不等式（x-b）2＞（ax）2的解集中的整数恰有三个，则实数a的取值范围为______.

解：由已知得（a2-1）x2+2bx-b2＜0恰有三个整数解，

则a2-1＞0，而a+1＞0，得a＞1，此时显然Δ＞0.

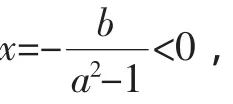
而（f0）=-b2＜0，（f1）=a2-1+2b-b2=（a+b-1）（a-b+1）＞0，

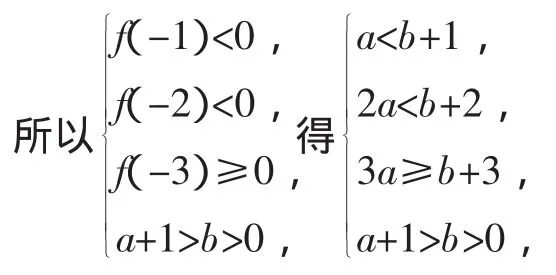
图2

作出其可行域，如图2，而直线a+1=b与直线2a=b+2的交点为（3，4），可知a∈（1，3）.

评注：本题与例1类似，构造出二次函数，在得到f（0）＜0，f（1）＞0后，根据其对称轴小于0，因此满足题意的整数解必然是-1，-2，-3，从而得到相应的条件.而对于二元不等式组求某一变量的范围，用线性规划知识得到a的范围，十分自然，明显比文［1］解法好得多.

例4（南通市通州区2013届高三寒假调研卷）已知使函数（fx）=x3-ax2-1（0≤a≤M0）存在整数零点的实数a恰有3个，则M0的取值范围是______.

解：由题意知x3-ax2-1=0对0≤a≤M0有三个整数解，

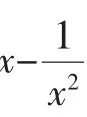
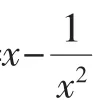
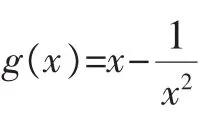
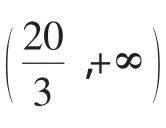
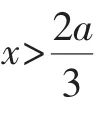
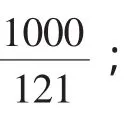
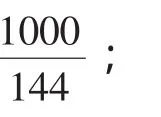
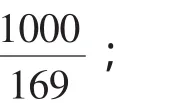
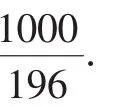
均符合a∈（0，10］.

不符合a∈（0，10］，因此当x≥16时也均不符合.

所以使（fx）=1000有整数解的实数a的个数为4个.

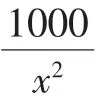
总结：例4是根据整数解的个数确定a的范围，而例5是由a的范围确定整数的个数（即a的个数），其实本质一样，即分离出常数后，构造的函数在一定范围内具有单调性，则满足要求的一个整数解必对应一个参数值.因此对于高次方程有整数解或高次函数有整数零点问题，由于涉及到参数，直接画图像会比较繁琐，不如分离参数后，考察所构造函数具有性质及相应图像，从而把握整数解与参数之间的联系，达到解题的目的.

1.任志鸿.十年高考分类解析与应试策略·数学［M］.海口：南方出版社，2009.