先设后求 以退为进——探讨平面翻折问题中“折起点”坐标的量化方略
2013-07-25☉
☉
笔者在运用空间向量解决立体几何中的平面翻折问题时发现,在建系之后的空间图形中,底面上各点的坐标相对容易量化,但折起之后,由底面上升到的空间的相应点(本文称之为“折起点”)的坐标,有时难以直接标注,而该点却往往是问题的核心之点,一旦坐标得以量化,则整个问题的难点随即“土崩瓦解”.因此,如何有效量化“折起点”的坐标是解决这类问题的关键.笔者探究发现,在“折起点”坐标难以直接标注的情况下,采用“先设后求、以退为进”不失为一种有效的方略,即欲求“折起点”坐标,先设其坐标为(x,y,z),由该点向底面引垂线(退回平面),垂足的坐标即为(x,y,0)(设底面为xOy平面),通过翻折问题的几何性质解出x,y;然后再返回到“折起点”中(进到空间),根据已知条件或翻折性质,求出坐标z,从而求得“折起点”坐标.由于在底面求解x,y时,须借助翻折问题的几何性质,为此,笔者下面先介绍相关性质,然后例谈如何具体求出“折起点”坐标.
一、性质介绍
平面翻折问题的实质是平面绕轴的旋转问题,因此,同一平面在翻折前与翻折后各几何元素间的位置、大小关系均保持不变,由此可推出如下性质:
性质1:如图1,将△ABC沿直线AB折起至△ABC1,则AB⊥CC1.
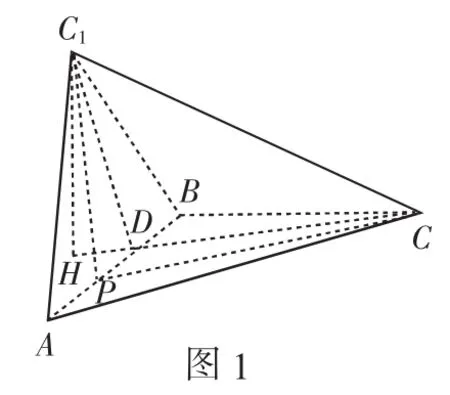
证明:过点C作CD⊥AB,垂足为D,连接C1D,则C1D⊥AB(因为C1D是CD经平面翻折后的线段),所以AB⊥平面C1DC,从而AB⊥CC1.
性质2:如图1,将△ABC沿直线AB折起至△ABC1,设折起点C1在△ABC所在平面内的射影为H,则HC⊥AB.
证明:因为C1H⊥底面ABC,所以AB⊥C1H,又由性质1知AB⊥CC1,所以AB⊥平面C1HC,所以AB⊥HC,即HC⊥AB.
性质3:如图1,将△ABC沿直线AB折起至△ABC1,设P是直线AB上任意一点,则PC1=PC.
证明:因为PC1是PC经平面翻折之后的线段,所以PC1=PC.
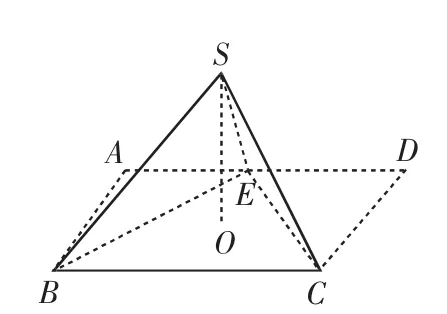
图2
性质4:如图2,四边形ABCD中,E是AD的中点,∠AEB=∠DEC, 将 △AEB、△DEC分别沿直线EB、EC折起至△SEB和△SEC,使得A、D重合于S点,设S在底面ABCD上的射影为O,则O在∠BEC的平分线上.
证明:因为∠AEB=∠DEC,折起后有∠SEB=∠SEC,故点O在∠BEC的平分线上.
二、方法应用
例1 如图3,在边长为3的正△ABC中,E、F、P分别是AB、AC、BC边上的点,满足AE=CF=CP=1,将△BEP、△CFP分别沿EP、FP向上折起,使边BP与边CP所在的直线重合(如图4),B、C折起后的对应点分记为B1、C1.
(1)求证:PF⊥平面B1EF;
(2)求AB1与平面AEPF所成角的正弦值.
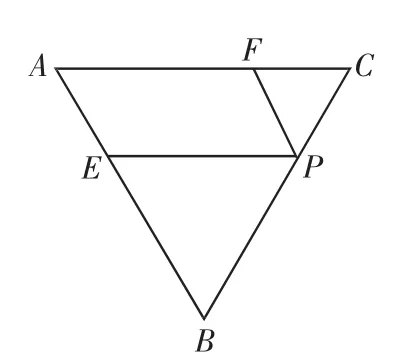
图3
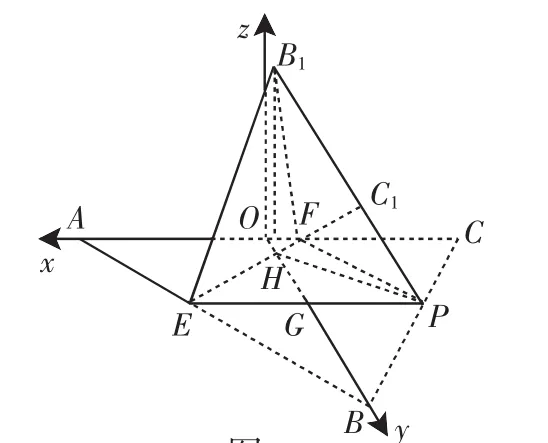
图4
解:(1)略;
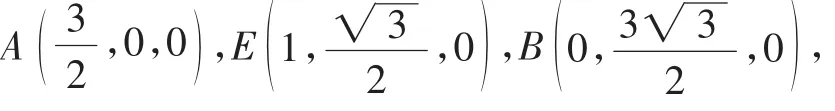
点评:本题建系之后,底面各点的坐标均容易标注,但“折起点”B1的坐标却难以直接标注,而由题意可知,一旦B1点的坐标得以量化,则后面的求解将是“一马平川”,否则,空间向量将无“用武之地”.既然如此,那就只得另辟蹊径:采取“先设后求、以退为进”.实践证明,这种方法不仅计算量小,而且操作简便,在空间向量遭遇“折起点”坐标挑战时,可巧妙化解,使问题的解决峰回路转、柳暗花明.当然,本题的解决离不开平面翻折问题的几何性质,因此,熟练掌握翻折问题的几何性质是解决此类问题的必备前提.
例2 如图5,有一边长为2的正方形纸片ABCD,E是AD边中点,将△ABE沿直线BE折起至A1BE位置,此时恰好A1E⊥A1C(如图6),点A1在底面上的射影为O.
(1)EO⊥BC;
(2)求直线A1C与平面A1BE所成角的正弦值.
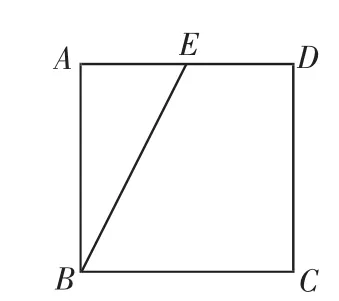
图5
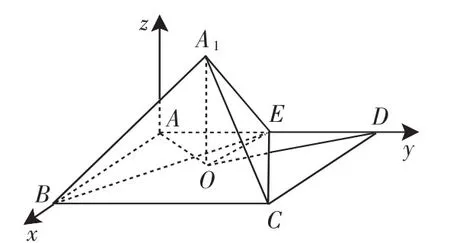
图6
解:(1)略;
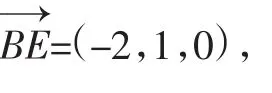
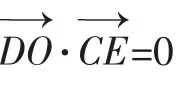
三、方法总结
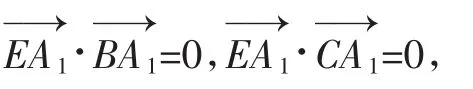
1.傅建红.平面翻折问题的若干性质及其应用[J].中学数学研究,2012(11).
2.沈良.例谈空间几何中翻折问题的解决策略[J].数学通报,2011(7).
