一种加权频域子空间模态参数辨识方法的改进

李永军 马立元 王天辉 段永刚

军械工程学院，石家庄，050003

0 引言

模态参数识别是指以模态参数模型为基础，以模态参数为目标的系统识别方法。由于模态参数较物理参数更能从整体上反映系统的动态固有特性，而且参数少得多，所以，模态参数识别是系统识别的基本要求，也是进行物理参数识别的基础［1－3］。

子空间辨识算法是近些年来出现的一类用于多输入多输出系统辨识算法的总称［3］。目前子空间辨识算法的研究以时域算法居多。时域子空间方法由于受到环境及测量噪声的影响，有时辨识效果并不理想，而频域子空间法得益于较为准确的频响函数估计，往往能提供理想的辨识结果［4］。频域子空间算法相对其他频域辨识方法而言，具有参数化、模型缩减和收敛性等优点，同时，采用较为准确、可靠的频域数据能达到很好的辨识效果。

1 频域子空间辨识算法［5－6］

离散时间系统的状态方程可描述为

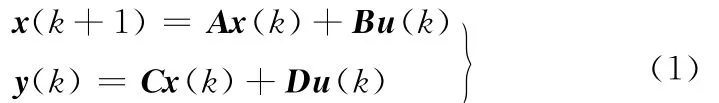
式中，x（k）为k时刻的状态向量；u（k）为k时刻的输入向量；y（k）为k时刻的输出向量；A为离散系统矩阵；B为离散输入矩阵；C为离散输出矩阵；D为传递矩阵。

对上式进行傅里叶变换：

式中，N为频率点数。

令Yre＝ ［Re（Y）Im（Y）］，Ure＝［Re（U）Im（U）］。其中，Re（·）表示复数的实部，Im（·）表示复数的虚部。

若将输出矩阵Yre正交投影到矩阵Ure的行空间的正交补空间Ure，⊥上，则有

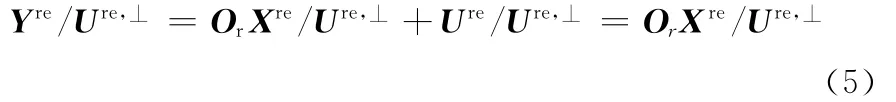
用“A/B”表示矩阵A到B的投影，构建矩阵［UreYre］并进行 QR分解，可得等式

对进行奇异值分解，可得到Or的估计值

式中，n为模型的阶次，系统的阶次常根据奇异值矩阵Σ中较大的奇异值个数确定。

根据最小二乘法估计矩阵A、C可得

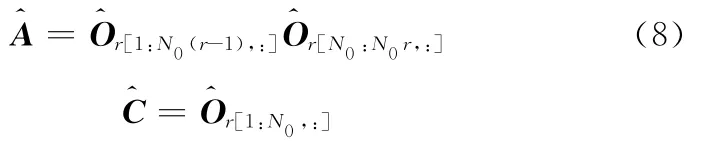
采用离散系统建模，模态频率、阻尼和振型的计算式为［7］：

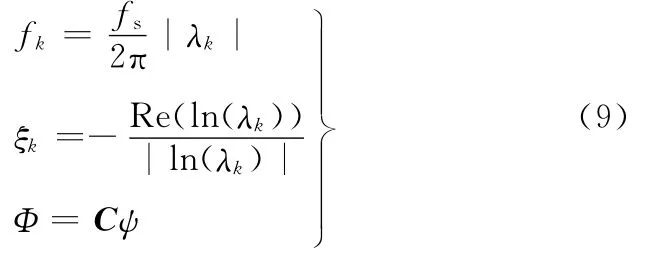
式中，fs为采样频率；λk为矩阵的特征值。

2 改进频域加权算法

频域子空间方法虽已被证明在解决模态分析应用中具有有效性，但其方法未考虑应用中的噪声影响。极大似然方法虽然对特殊的噪声模型有很好的理论保证，但计算过程中会遇到关于未知参数的非线性方程，需要有一个迭代过程，因此这种方法运算量较大，且需考虑其收敛性。因此，本文将研究频域子空间算法的噪声抑制问题。

当系统中加入观测噪声或干扰噪声时，采用频域子空间方法对系统模态参数的辨识将会产生较大的误差，甚至无法识别。下面以文献［4］中的两输入两输出系统为例进行阐述，系统矩阵参数为

可以计算得出：该系统有2个模态，其对应的模态参数分别为：f1＝0.1275Hz，ξ1＝0.1987；f2＝0.3761Hz，ξ2＝0.0680。

采用扫频激励，扫频初始频率为［0.1，0.1］Hz，终止频率为［2，2］Hz，扫描时间为［20，10］s。采样频率为1Hz，数据长度为1024。向输出加入白噪声，噪声方差为［0.2，0.2］，采用频域子空间算法进行系统模态参数辨识。辨识结果与理论值对比如表1所示。所得传递函数与理论值对比如图1所示。

表1 辨识结果与理论值对比

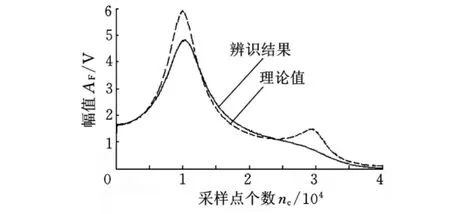
图1 加入白噪声后的频域子空间辨识传递函数与理论值曲线

从辨识结果可以看出，如系统中混入噪声，频域子空间辨识算法的精度将受到较大影响。因此，需要考虑系统去噪。除传统的原始信号去噪方法外，还可采用加权方法控制噪声的影响。

为减小噪声带来的方差，本文提出一种加权的频域子空间模态参数辨识算法。

在绝大多数测量中，输入和输出的信噪比在不同频带上是不相同的，即使相同，也具有很强的相关性。该方法的基本思想是增大噪声较小频点上的能量，减小噪声较大频点上的能量，从而提高模态参数的辨识质量。频率点上的噪声以该点数据多次实验的方差为依据，方差大者则其噪声较大，反之则较小。

假设在系统的输入端和输出端均存在噪声，噪声方差（k）是不可知的，但可以从实验数据中提取得到。这样，实际的方差就由采样估计值代替。其值只能通过统计的方法获得。本文首先对噪声方差进行估计。

若进行M次实验，则离散傅里叶变换（DFT）可表示为

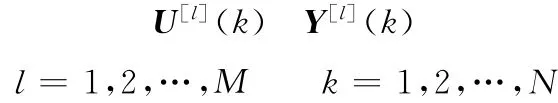
采样频域特性均值计算表达式为

用均值表示的噪声方差为

令

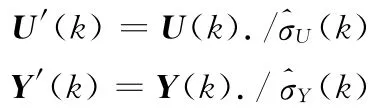
式中，“./”表示点除；U′、Y′分别为加权后的输入和输出矩阵。将U′和Y′分别取代系统方程中的U和Y，则

式（12）为加权后的广义状态方程。

通过加权，则

由式（15）可以看出，通过对输入U的加权，实现了对构成Ure的Q′1的行空间进行修正，利用行空间投影关系：

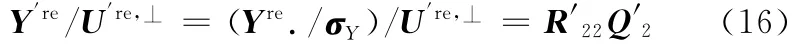
通过引入σY对R22进行修正和上述加权处理，噪声方差较小的频率点上的信号能量相对加强，而噪声方差较大的频率点上的信号能量相对减弱，从而降低了噪声对辨识结果的影响。

3 加权算法仿真结果

为说明问题，采用上述的系统模型进行仿真验证。向输出加入［0.2，0.2］的白噪声方差，采用加权频域子空间辨识算法获得的系统模态参数如表2所示，其传递函数如图2所示。

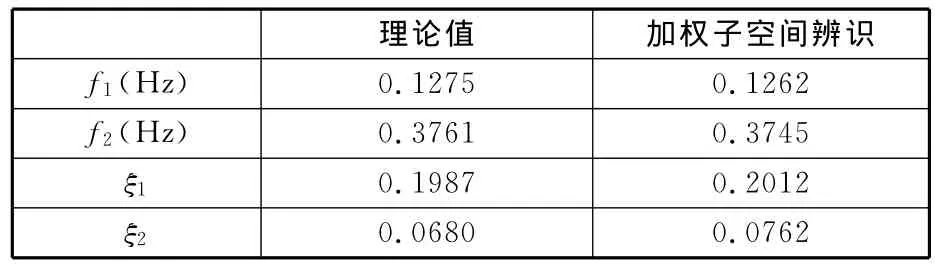
表2 加权子空间辨识算法辨识结果

向归一化的输出信号加入有色噪声，由方差［0.2，0.2］的白噪声通过通带频率0.3～0.4Hz的带通滤波器产生。采用基本算法和本文提出的加权辨识算法获得的系统传递函数的幅频特性如图3所示。

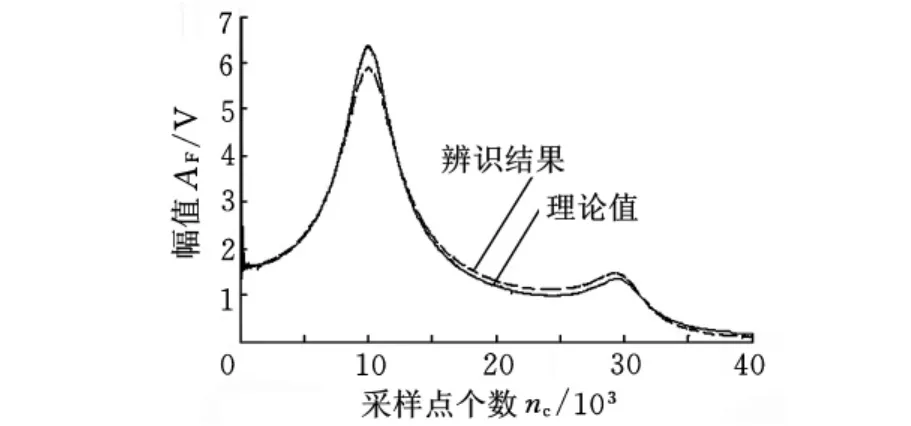
图2 加权子空间辨识算法辨识传递函数与理论值曲线

图3 加有色噪声的辨识传递函数与理论值曲线

4 某变截面轴的模态参数识别

某装备的传动部件受环境、自身转速等因素影响，经常出现故障。为了降低故障率，要使传动轴的转速避开其固有频率，因此有必要对传动轴的模态参数进行辨识。

实验对象是一个横截面为方形的变截面轴结构，材料为45钢，传感器及激励点如图4所示。由于该轴的对称性，可以只考虑其弯曲模态，减少传感器数量需求。

图4 测点布置及激励

在进行模态分析实验时，采用自由悬挂方式。对实验对象采用力锤进行激振。为模拟白噪声激励，力锤敲击时的部位和力量均随机。采样频率为20kHz，每个响应信号取20 000个采样点。实验时利用DH5920动态信号测试仪获取响应数据，利用MATLAB软件编程实现模态参数识别。系统阶次根据SVD分解结果确定为8阶。进行加权频域子空间算法辨识时的试验次数为10次。

有限元计算（FEM）能够使分析者对该框架结构的特征有初步了解，也可以为实验室的测试工作和参数辨识计算提供参考，使分析者在实验之前就能够大致掌握振型节点的所在之处以及结构的基本振型情况。小型简单金属结构实验已经验证了有限元计算结果的可靠性及准确性［6］。该变截面轴结构简单，可以将有限元计算结果作为真实值。识别所得前四阶模态参数与有限元计算结果对比如表3所示。图5～图8所示为频域加权子空间辨识方法识别的振型和ANSYS计算的振型结果。采用有限元计算振型矢量和辨识所得振型矢量进行模态置信度（modal assurance criterion，MAC）分析［8］。有限元模型缩聚采用Guyan方法实现，加权频域子空间辨识所得振型向量与有限元缩聚后的振型向量之间的MAC值柱状图如图9所示。

表3 频域子空间方法辨识结果与有限元结果比较

图5 第一阶振型对比

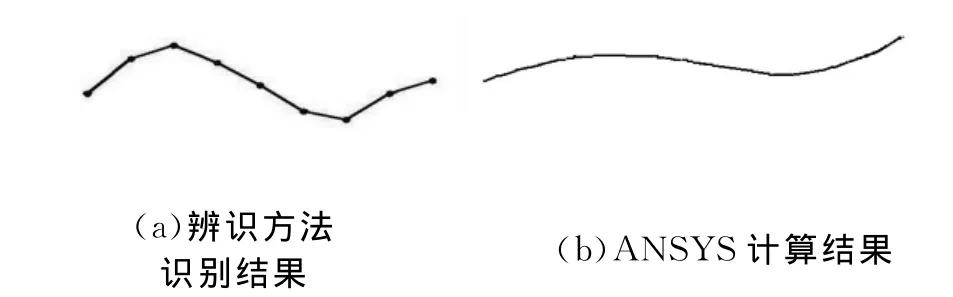
图6 第二阶振型对比

通过表3和图5～图9对比发现，实验模态参数识别得到的各阶模态参数与有限元分析得到的分析模态参数基本一致，证明本文研究所采用

图7 第三阶振型对比

图8 第四阶振型对比

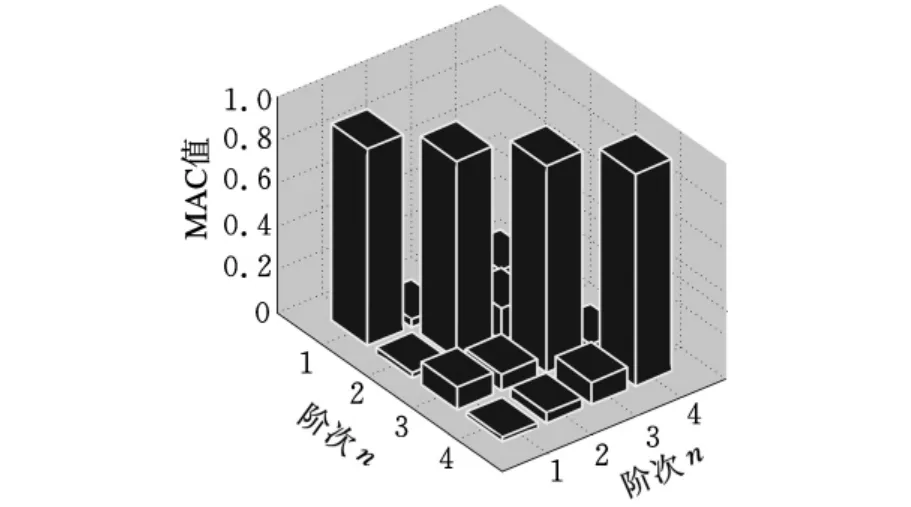
图9 辨识结果与有限元计算的MAC值

的模态参数识别方法是可行的，所得模态参数反映了该部件的动态特性。

5 结束语

本文通过研究频域子空间算法，提出了一种对其加权的模态参数识别方法，其有效性及准确性被实验分析所证明。

该算法能够获得相对准确的模态参数，能够减少计算量和节约计算资源。采用该方法时，应使用尽可能大的数据长度，以保证较为准确的傅里叶变换结果。该方法还可为其他结构的动态特性快速评价和可靠性优化设计提供参考。

［1］孟杰，陈小安，陈锋.高速电主轴的试验模态分析［J］.机械设计，2009，26（6）：70－78.

Meng Jie，Chen Xiaoan，Chen Feng.Experim Entalmodality Analysis of High Speed Motorized Spindle［J］.Journal of Machine Design，2009，26（6）：70－78.

［2］常军.随机子空间方法在桥梁模态参数识别中的应用研究［D］.上海：同济大学，2006.

［3］刘东霞.基于随机子空间法的梁桥模态参数识别［D］.成都：西南交通大学，2008.

［4］唐炜.飞机颤振模态参数识别方法研究［D］.西安：西北工业大学，2006.

［5］Schoukens J，Pintelon R.Estimation of Nonparametric Noise Models［C］//IEEE Instrumentation and Measurement Technology Conference.Sorrento，Italy，2006：102－106.

［6］Mckelvey T.Subspace Methods for Frequency Domain Data［C］//In Proceeding of the 2004American Control Conference.Boston，Massachusetts，USA，2004：673－678.

［7］樊江玲.基于输出响应的模态参数辨识［D］.上海：上海交通大学，2007.

［8］王天辉，马立元，李世龙，等.基于灰并联模态柔度曲率差的梁结构损伤识别［J］.中国机械工程，2012，23（7）：790－793.

Wang Tianhui，Ma Liyuan，Li Shilong，et al.Damage Identitication of a Beam－type Based on Grey Relation Modal Flexibility Curvature Difference［J］.China Mechanical Engeering，2012，23（7）：790－793.