基于有限元法的球形数控电解加工工艺试验研究

刘德营 傅秀清 康 敏 董朝盼

1.南京农业大学，南京，210031 2.江苏省智能化农业装备重点实验室，南京，210031

0 引言

数控电解加工兼有传统电解加工和数控加工的优点，避免了复杂成形阴极的设计与制造，投产周期短，适用加工范围广，具有很大的加工柔性，可用于小批量、多品种甚至单件试制的生产中。在数控电解加工过程中，阴极上参与加工的区域与拷贝式加工相比大为减小，使得电解液中产生的气体及热量的影响显著下降，因而可提高加工精度和表面质量［1］。目前，国内对数控电解加工成形规律的研究主要集中在利用直线刃阴极加工整体式叶轮中的阴极运动对加工间隙及精度的影响上，且取得了一些研究成果［2－3］。国外则有利用球形阴极或板状阴极进行曲面加工的研究［4－5］。由于数控电解加工过程中阴极作相对复杂的运动，从而使得分析其成形规律变得较为困难，传统的平衡间隙法也受到了很多限制。

本文采用有限元法在计算机上模拟球形阴极电解加工的过程，可以分析不同时刻，尤其是开始、过渡、稳定平衡3个不同阶段在加工区域内的电场分布，为数控电解加工阴极轨迹规划、加工工艺参数选择以及加工精度的分析提供了研究方法和理论依据。

1 球形阴极数控电解加工原理

电解加工是基于金属在电解液中发生阳极溶解的原理将零件加工成形，加工过程中工具阴极无损耗、无切削力。球形阴极的数控电解加工是利用简单形状的内喷式球形阴极，通过计算机控制阴极相对工件的运动来加工型面，其加工原理如图1a所示。加工时，工件接直流电源的正极，球形阴极接直流电源的负极，电解液以一定压力进入阴极进液口，经阴极流道，从球面的小孔喷出进入加工间隙，发生电化学反应，去除材料［4］。图1b为紫铜材料制成的球形内喷式阶梯腔阴极及其结构示意图，球面半径为5mm，其上有6个孔径为1mm的出液口。

2 加工过程有限元模型的建立

在球形阴极数控电解加工中，加工电压U、初始加工间隙δ0、阴极进给速度vp为影响切削深度x的主要工艺参数。本文通过球形阴极在水平方向上进给时的加工过程仿真，研究其加工机理，过程示意图如图2所示。球形阴极在工件表面上沿直线O1O2水平进给，初始加工间隙为δ0，如图2a所示；经过一段时间t之后，阴极以进给速度vp由初始位置O1处沿直线运动至O2处，工件型面因电解反应而发生变化，最终型面为曲线A1A2，其切削深度为x，如图2b所示；在此过程中，阴极在数控系统的控制下沿轨迹直线O1O2运动，阴极球面中心处C点的轨迹如图2b所示。直线C1C2因在阴极进给加工过程中C点轨迹所对应的切削深度不变，故其加工轨迹相同，如图2c所示。

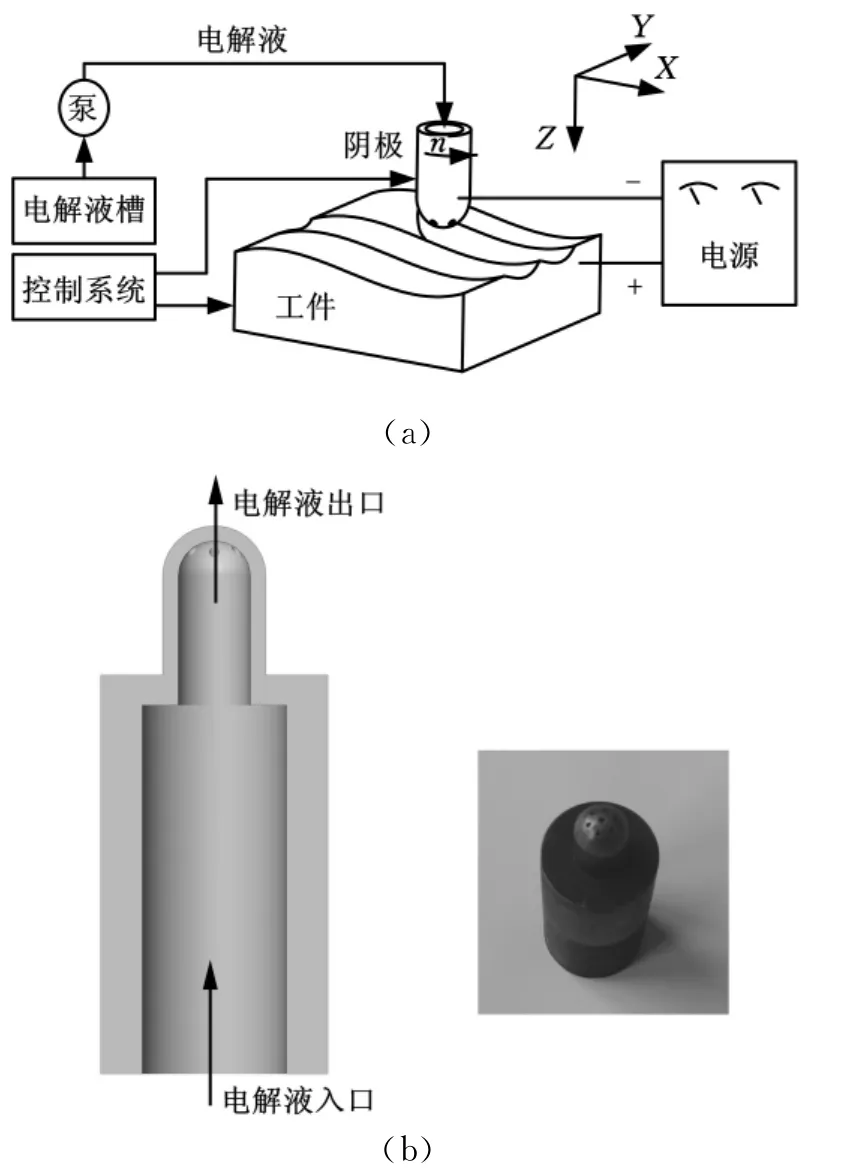
图1 球形阴极数控电解加工原理及球形阴极实物图

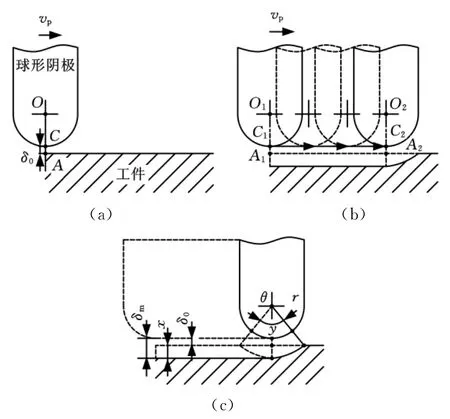
图2 阴极水平进给的加工模型示意图

法拉第定律是进行工件型面成形和预测过程定性分析和定量计算的基础理论，主要包括：

（1）在电极的两相界面处发生的电化学反应的物质质量与通过其界面的电量成正比，即法拉第第一定律。

（2）在电极上溶解或析出一克当量任何物质所需的电量相同，与该物质的本性无关，即法拉第第二定律。

基于上述分析，本文在ANSYS中建立的球形阴极水平进给加工间隙二维电场分布模型如图3所示。其中，Γ1为球形阴极运动轨迹的边界，Γ2为工件阳极的上表面边界，Γ3、Γ4、Γ5、Γ6为自由边界，与Γ1和Γ2形成了阴极和阳极之间的封闭区域Ω。为简化求解过程，做如下假设：

（1）加工间隙内电解液电导率为常数。

（2）忽略边界效应，认为极间电场为近似的稳恒电流场［5］。

图3 阴极加工间隙内电场的分析模型

对封闭区域Ω进行电场分析，结合电场和电解加工理论，封闭区域Ω内各点的电势分布φ（x，y）满足拉普拉斯方程，即

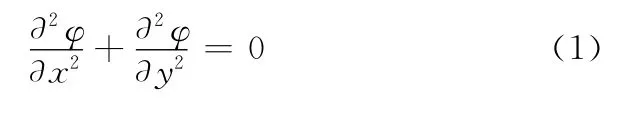
式中，φ为电场中各点的电位。

因工件阳极接电源正极、球形阴极接电源负极，故在阴阳极表面均为等势面，设为第一类边界，即

除阴极、阳极边界外，其他边界为构建的自由边界，以形成封闭的求解区域Ω，在这些边界条件上施加第二类边界条件：

有限元法求解过程如下：

（1）建立有限元模型、划分网格、加载求解得到工件阳极上表面Γ2上各点的电流密度。

（2）将整个加工时间离散化为各个微小时间段δt，并假设在微小时间段δt内，电场发生的变化可以忽略不计，在阳极上表面边界Γ2上的各点电流密度不变，加工速度不变。

根据法拉第定律，工件阳极上表面边界Γ2各点An（XAn，YAn）的材料去除速度为

式中，η为电流效率；ω为电化学当量；iAn为Γ2上各点的电流密度。

经Δt时间后，工件阳极上表面边界Γ2各新点Bn（XBn，YBn）的坐标为

式中，iAnx、iAny分别为电流密度iAn在X 轴和Y轴上的分量。

以这些新点Bn（XBn，YBn）建立新的阳极上表面边界Γ2，重新回到第一步建立有限元模型进行求解，如此往复，直至加工结束，则可以求得整个加工过程中各个时刻的阳极表面加工曲线及电流密度。

3 有限元模型的求解结果

在实际加工过程中，由于电解质的种类、电解液流场的参数（如流量、压力、流速等）对加工有较大影响，本文中这些影响通过式（5）中的电流效率η来体现。在ANSYS软件中球形阴极电解加工过程模拟计算的详细过程及相关参数设置如下：

（1）选择分析类型为电场分析。

（2）设定单元及材料的属性。单元取PLANE230单元，最小边长取0.2mm；阴极材料为紫铜，其电阻率为17.5μΩ·mm；阳极材料为1Cr18Ni9Ti，其电阻率为730.0μΩ·mm；其电解液中NaCl的质量分数为12%，其电阻率为62.5Ω·mm，相对介电常数为70。根据文献［1］，使用NaCl溶液在材料1Cr18Ni9Ti上进行拷贝式电解加工时，一般取电流效率η＝0.61，故本文将首先取η＝0.61进行仿真分析。

（3）建立模型。建模时将工件阳极上表面边界Γ2分为260个关键点，并用样条曲线连接。

（4）划分网格。将各种材料附在模型中相应的表面上，选择自由网格进行网格划分。图4a所示为初始时刻模型的网格划分。

（5）加载求解。在阳极工件上加载电压12V，工具阴极上加载电压0V，初始时刻各节点电流密度的计算结果如图4b所示。

（6）时间间隔取12s，加工效率为61%，由式（6）、式（7）计算得到阳极表面上加工后各点的坐标。

（7）以第（6）步求得的新点作为阳极表面关键点，回到第（3）步进行下一个时间间隔的计算，直至加工结束。本文以120s时得到的仿真结果为例进行说明，如图5所示，图5a所示为120s时模型的网格划分，图5b所示为120s时各节点上的电流密度求解结果。

图4 初始时刻时网格划分及电流密度计算结果

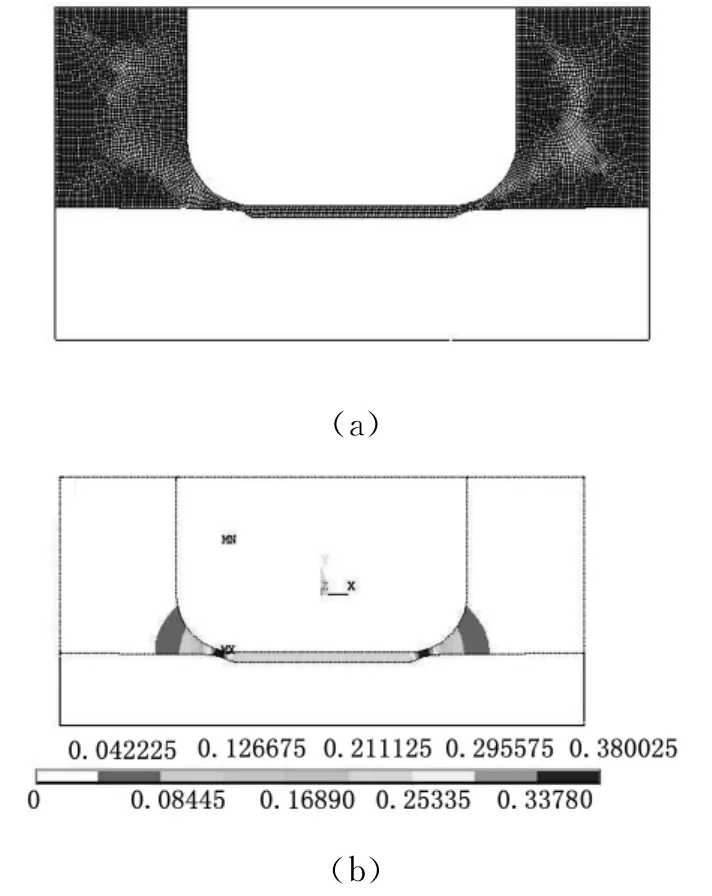
图5 η＝61%时网格划分及电流密度计算结果

由后续的试验测量结果可知，当工作电压U＝12V、初始间隙δ0＝0.1mm、阴极进给速度vp＝50mm／min时，切削深度x为0.23mm，但由图5计算可知，当η＝61%时切削深度x的求解结果为0.74mm，远远大于试验结果的实测值0.23mm，考虑到在实际加工过程中，电解质的种类、电解液流场的参数对电流效率和加工效率有较大影响，在本文中阴极与工件相对运动，其加工间隙内的流场处于不断变化的状态，故分析认为其电流效率应低于阴极静止状态时的电流效率。为确定电流效率值的范围，本文分别取η为50%、40%、30%、20%、10% 进行计算，求解得到的阳极型面变化曲线如图6所示。由图6可以看出，当η＝20%时得到的求解值与试验的实测值比较接近，故其后，在本文的有限元分析中均取电流效率η＝20%进行求解计算。

图6 取不同电流效率时阳极型面的计算结果

4 工艺试验及分析

本文采用固定其中2个参数，改变单个参数取值范围的方法进行工艺试验，可得到单个工艺参数对切削深度值的影响曲线，并与该参数组合在仿真中得到的理论值进行对比分析，以验证有限元模型的准确性，总结球形阴极数控电解加工的工艺规律。文中加工电压U的取值范围为8～24V，初始加工间隙δ0的取值范围为0.1～0.65mm，阴极进给速度vp的取值范围为15～70mm／min。分别进行工艺试验和有限元模型求解，得到的切削深度的计算值和实测值的对比曲线如图7所示。

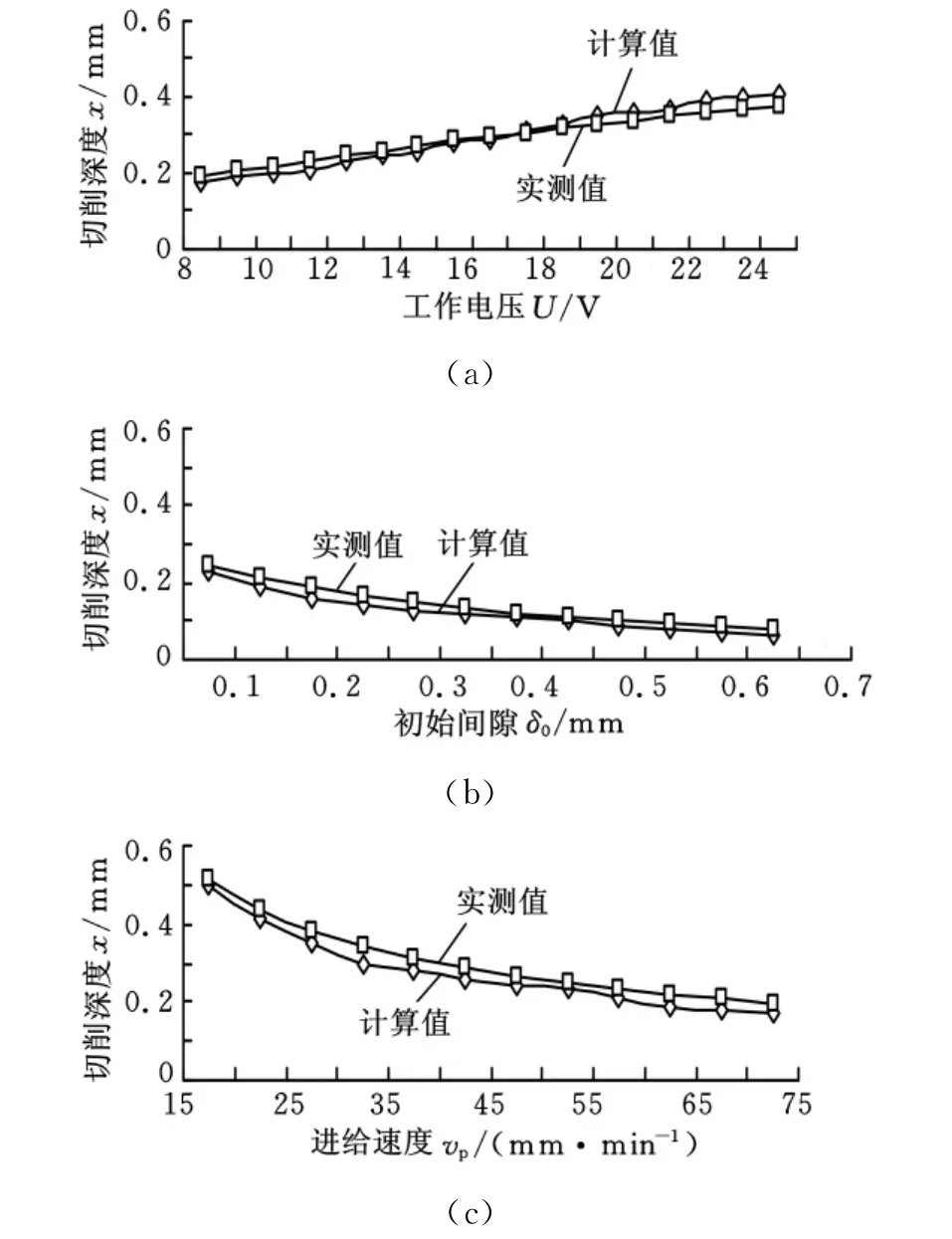
图7 切削深度计算值与实测值的对比曲线

图7a所示为不同工作电压下得到的切削深度计算值与实测值的对比曲线，从图中可以看出切削深度值随工作电压的增大有明显的增大趋势；图7b所示为不同初始间隙下计算值与实测值的对比曲线，从图中可以看出切削深度值随初始间隙的增大有明显减小的趋势；图7c所示为不同阴极进给速度下计算值与实测值的对比曲线，从图中可以看出切削深度值随阴极进给速度的增大有明显的减小趋势。采用有限元法得到的切削深度的计算值与试验实测值随各工艺参数变化的趋势基本一致，误差相对较小，验证了有限元求解模型的准确性，对评定和预测在一定工艺条件下的球形阴极数控电解加工工件型面质量具有实际应用意义。

5 结束语

本文提出了基于有限元法的电解加工过程模拟思路和方法，通过在ANSYS中建立球形阴极数控电解加工过程的二维电场模型进行求解计算，得到工件阳极表面不同时刻的电流密度分布和型面变化形状，以过程模拟中的工艺参数进行工艺试验，检测加工型面的尺寸值，并与理论模拟值相比较，验证了有限元求解模型的准确性。试验结果表明，该方法可以满足工程计算的要求，为深入开展球形阴极数控电解加工过程的研究提供了方法和理论依据，对评定在一定工艺条件下的数控电解加工工件型面质量具有指导意义，利于进行复杂型面电解加工时加工过程的控制、误差分析和阴极路径优化等方面的研究。

［1］徐家文，云乃彰，王建业，等.电化学加工技术——原理、工艺及应用［M］.北京：国防工业出版社，2008.

［2］李志永，朱荻，孙春华，等.发动机叶片电解加工阴极设计有限元数值解法研究［J］.中国机械工程，2004，15（13）：1151－1154.Li Zhiyong，Zhu Di，Sun Chunhua，et al.Study on Finite－Element Arithmetic in Electrochemical Machining for Turbine Blades［J］.China Mechanical Engineering，2004，15（13）：1151－1154.

［3］王蕾，朱荻.基于有限元数值方法的电解加工工件型面的预测［J］.中国机械工程，2006，17（9）：927－930.Wang Lei，Zhu Di.Determination of Anode Shape Based on Finite Element Method in Electrochemical Machining［J］.China Mechanical Engineering，2006，17（9）：927－930.

［4］傅秀清.球形阴极数控电解加工关键技术研究［D］.南京：南京农业大学，2010.

［5］Yang Y，Kang M，Fu X Q.Research on the Process of NC－ECM with Ball－end Cathode Based on FEM［J］.Key Engineering Materials，2011，458：93－98.