基于时域同步平均法的行星齿轮振动信号分离技术
2013-07-25胡贵锋王细洋
胡贵锋 王细洋
南昌航空大学,南昌,330063
0 引言
行星齿轮应用非常广泛,相比太阳轮和滚动轴承,其信号采集及故障诊断更为困难。文献[1-3]介绍了行星齿轮箱故障诊断的各种方法,但大多针对轴承和太阳轮。对于行星轮系,行星齿轮既围绕自身轴线自转,也围绕中心轮公转,行星齿轮相对于振动传感器的位置是变化的,因而在不同时刻采集的振动信号是变化的。行星轮数量往往不止一个,所以测得的振动信号是不同旋转位置行星轮和中心轮振动信号的叠加。齿轮故障产生的信号脉冲和信号扭曲往往被其他信号所掩盖,因此很难获取。
本文通过对行星轮系传动系统的研究,找出了行星轮系的传动规律,结合加窗和时域同步平均方法能较快地得到行星齿轮振动信号。
1 时域同步平均理论
时域同步平均法[4](time-domain synchronous average,TSA)是一种有效的信号预处理方法,它通过将齿轮箱振动的采样信号与待分析齿轮的转速同步并进行叠加、平均而获得信号。该方法可以消减其他齿轮信号和外界噪声,增强待分析齿轮的振动信号。
设有间隔为Δt的采样序列x(n),n=0,1,…,N,若采样周期为T,则时域平均表达式为
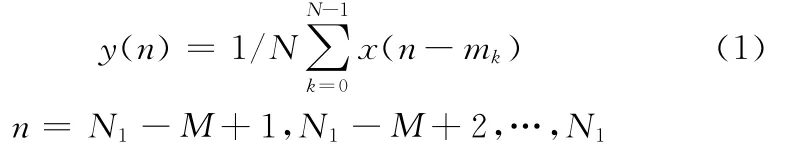
式中,N1为每圈采样点数;y(n)为平均后得到的新序列,其长度为M=T/Δt的就近取整值;mk为kT/Δt的就近取整值;N为平均段数。
由白噪声的不相关性可知,经过时域同步平均后,随机噪声功率降为原来的1/N,即信噪比可提高1/。
2 行星齿轮信号分离方法
2.1 行星齿轮振动理论
行星齿轮振动信号在提取上存在2个难点[2]:第一,传感器安装在箱体上,信号受位置影响;第二,行星齿轮相对于减速箱(传感器)而运动,信号难以采集。
如图1所示,行星齿轮与太阳轮和齿圈同时啮合。由于齿圈是固定的,行星齿轮的一个齿在行星齿轮旋转一定圈数后,该齿又会和齿圈上起始与之啮合的齿再次啮合。本文把这个最小的圈数[5]定义为Nm,g,其数学表达式为
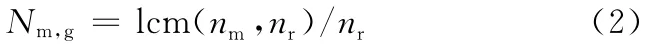
式中,lcm表示求最小公倍数;nr为齿圈齿数;下标g表示行星轮或太阳轮;nm为行星轮或太阳轮的齿数。
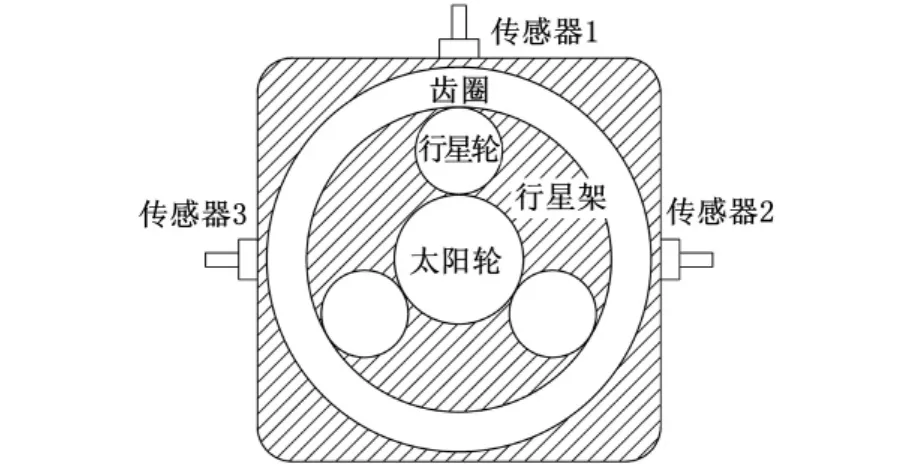
图1 行星齿轮箱传动简图
式(2)可表示为最小公倍数是齿圈齿数的Nm,g倍,这样在Nm,g范围内,齿圈齿数nr刚好可以回到起点,指定的行星齿p1与指定的齿圈上的齿r1在旋转方向上对准,每Nm,g圈中,会啮合一次。当Nm=1时,则行星架旋转一周,啮合一次,当Nm>1时,则行星齿p1大于1圈才会与齿圈上的齿r1啮合。因此,行星齿轮上不同的齿与指定的齿圈上的齿的依次啮合可用齿的序列公式表示为

在初始状态下,即在n=0时,可得T0,g=1,故可认为是行星齿r1与齿圈p1啮合,依次可计算齿圈与下一圈的啮合行星齿序。上述公式为行星齿轮箱齿序的计算提供了理论依据。
2.2 窗函数的选择
窗函数能修正信号的非周期性,并减小频谱中由于泄露而带来的测量不准确性。快速傅里叶变换假定时间信号是周期无限的,但在分析时往往只截取了其中的一部分,因此需要加窗以减小泄露。本文中的窗函数必须满足2个参数要求:第一,窗宽,需包含行星齿的一个齿宽;第二,窗形,即窗函数的形状必须与行星齿轮的振动信号特征在时域上的表现类似或接近才可以减少泄露和误差。图2所示为行星齿轮信号特征,在其中的矩形窗、汉宁窗、三角窗、Tukeywin窗中,只有Tukeywin窗上端有比较明显的突起,与行星齿轮信号特征类似,因此本文选择Tukeywin函数[6]进行加窗处理。
2.3 行星齿轮的振动分离方法
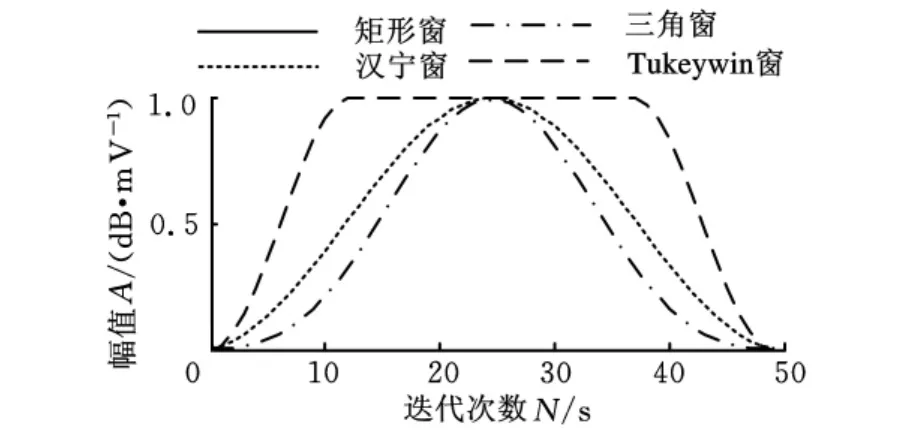
图2 不同窗函数的形状
行星齿轮的齿信号分离主要采用加窗获取的方法,其流程如图3所示。首先通过传感器连续采集行星齿轮振动信号,传感器采集一整圈的振动信号包括行星齿轮Ⅰ、Ⅱ、Ⅲ号的信号,选取一经过传感器的行星齿轮周期信号作为一个加窗宽度[7](图3a),计算单个行星齿齿宽(图3c),计算方法如下:
假设Ns为转速,fs为采样频率,ip,s为行星轮与太阳轮的传动比,Zp、Zr、Zs分别为行星轮、齿圈和太阳轮的齿数,fp为行星齿轮啮合频率,fH为行星架的啮合频率,则行星齿轮转动频率Fp为
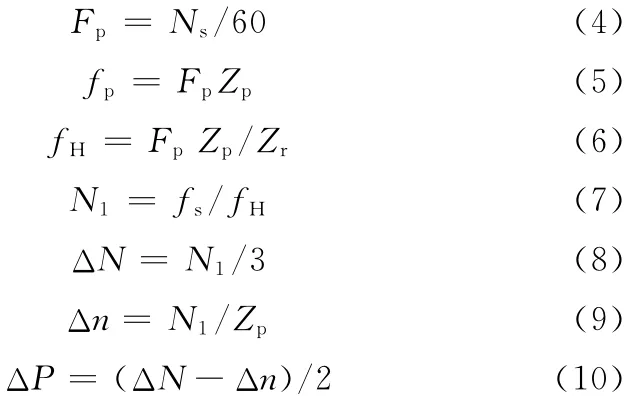
式中,ΔN为传感器采集的行星齿轮信号宽度,Δn为单个行星齿信号宽度,ΔP为窗口平移宽度。
平移ΔP后,以Nm,g圈为一个周期,设Nz为总采样点数,则总采样圈数Nr为

总采样圈数,即为总平均段数。采集实验所需传感器个数表达式为

根据上述时域同步平均原理,进行叠加平均,得到如图3d所示的行星齿轮信号图。齿序根据式(3)计算出来的顺序进行调整,通过编程,使得分离出来的32个行星齿信号对应式(4)的顺序从小到大依次调整,从而获得本实验所需的信号。
3 行星齿轮振动信号实验验证
3.1 参数计算
本文实验台采用了一台输入功率为4.5kW,转速为Ns=1430r/min的交流电动机。编码器的采样频率为fs=3600Hz,整周期采集,按一定格式存储。齿圈齿数为Zr=71,行星轮齿数为Zp=32,太阳轮齿数为Zs=12,行星齿轮与太阳轮的传动比为ip,s=6,行星齿轮转频及行星架啮合频率分别为
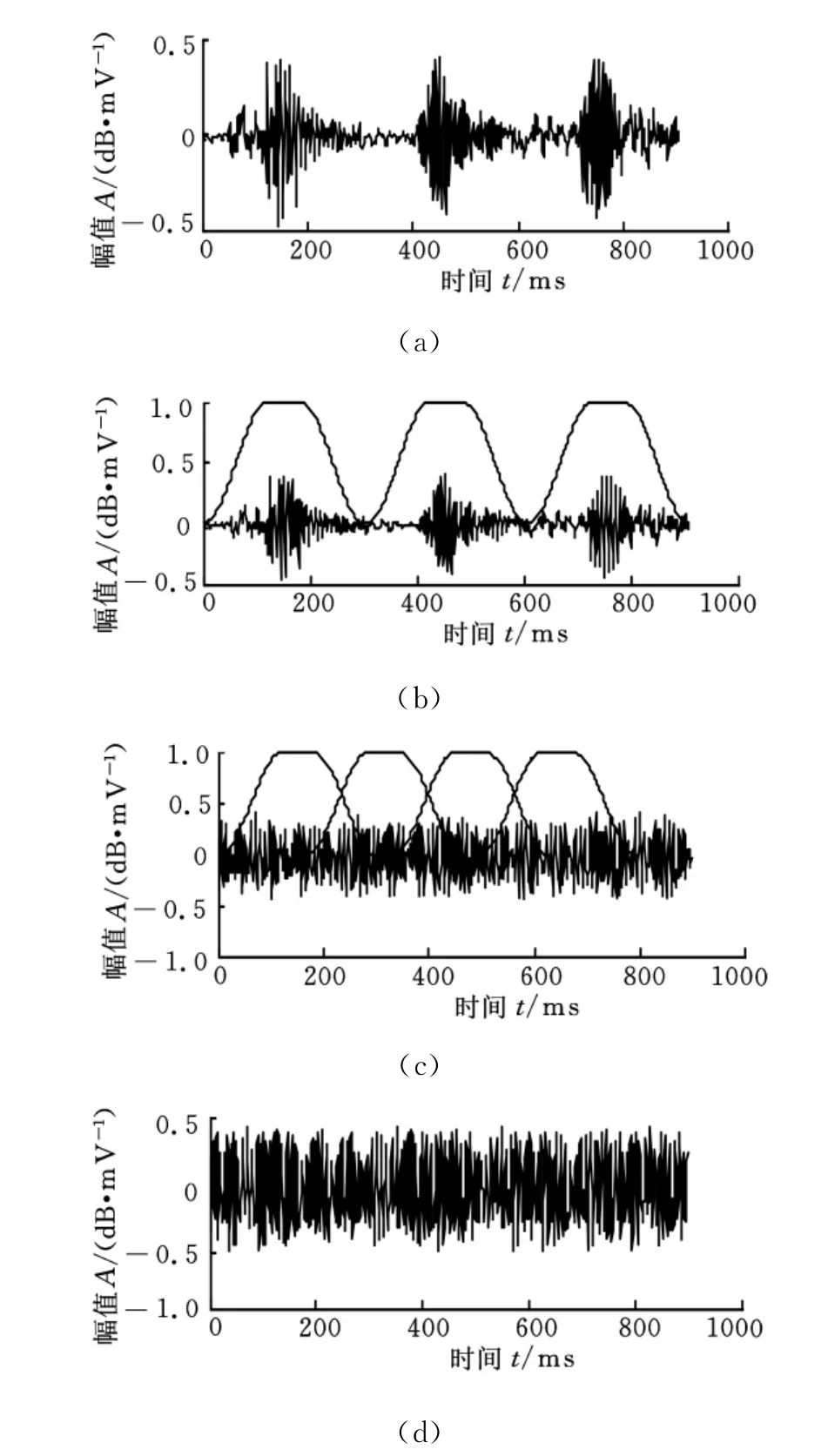
图3 行星齿轮信号分离流程图

N1≈907,ΔN≈302,Δn≈28,ΔP=137,Nm,p=32,Nm,s=12,总采样圈数Nr≈397。根据式(12)可得Np=1,Ns=3,即采集行星齿轮信号所需数量为1个,采集太阳轮信号需要3个,本文实验不考虑太阳轮,则下标g变为p。根据式(3)得到的特定行星齿与特定齿圈齿啮合序列如表1所示。

表1 行星齿与齿圈齿啮合序列
从表1可以看出,全部行星齿都会经过某一给定的齿圈齿,因此需要一个传感器,为确保信号的稳定性和较短的采样时间,可根据条件允许增加传感器个数。nx表示行星齿顺序,即序列为第nx圈的齿圈r与行星齿p的啮合状态。
3.2 实验分析与对比
实验台如图4。本文实验采用3个传感器分别对行星齿轮减速箱内的3个行星齿轮进行故障信号提取,3个传感器与圆周相隔90°,将两行星齿轮的间隔设置为120°,因此其振动信号也相差120°,图5所示为3个传感器采集的一圈行星齿轮信号。行星齿从远到近靠近传感器,波形从小到大,在没有破损的行星齿轮中,波形的波峰和波谷位置为最靠近传感器的那个齿。

图4 实验台及其组成部分
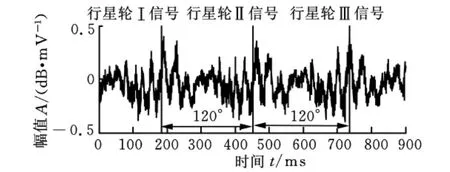
图5 行星齿轮旋转一圈产生的信号
图6所示为行星齿轮的频谱图,图中的行星齿轮啮合频率为130Hz,与127Hz接近,2倍频258Hz和3倍频380Hz。齿轮啮合频率主要集中在3倍频处,啮合频率由于调制等因素受到抑制,在图6中显示数值很小。对采集的行星齿轮Ⅰ的前9个行星齿信号先加Tukeywin窗,如图7所示。先对采集到的原始信号做加窗处理,获取完整行星齿信号;然后做时域同步平均;最后得到行星齿波形图。根据齿的啮合序列进行调整(表1),组成一个新的行星齿波形图,如图8所示。

图6 行星齿轮信号频谱图
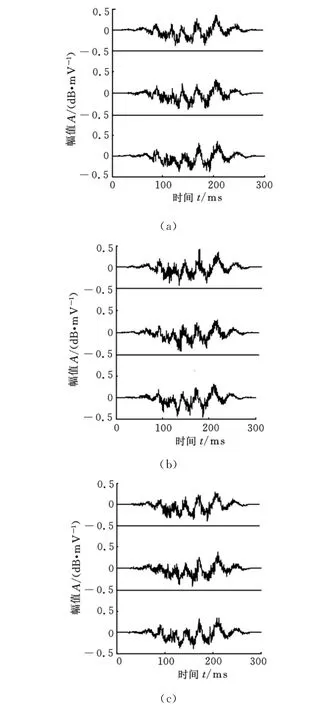
图7 加Tukeywin窗后的波形图

图8 行星齿轮Ⅰ、Ⅱ、Ⅲ时域图
通过上述时域和频谱图可以看出,平均后的时域信号反映了行星齿轮的运行状态。图8为326个行星齿的振动信号,反应了行星齿的振动情况。理论状态下,每个齿的信号都应一样,但实际中,因信号的不确定性以及调制和不对中等原因都会致使齿信号出现偏差,但偏差一般都在误差范围之内。由于所用行星齿是完好的,啮合频率周边边频带较少。从总体上看,该方法是行之有效的。
采用对行星齿轮原始信号进行功率谱分析的方法开展对比实验,如图9a所示,由图可以看出行星齿轮运行时啮合频率fs及其倍频周围围绕着不规则的边频带,排除破损情况,说明采样时间内各种振动噪声较大,与图6对比可知,时域同步平均前后的啮合频率得到突显,未受损情况下的边频带很少,噪声得到较大抑制,运行较为平稳。图9b为谱平均后的倒频谱图,低倒频谱段t1=17ms,t2=27ms,t3=39ms,t4=68ms。行星轮转速Np=Ns/ip,s= 1430/6 ≈ 38r/min,T1=Np/t1=238/17≈14Hz,与127Hz相差较大,且各频率(边频带)间隔不规律,没有体现出转频的特性,故时域同步平均法更为有效。
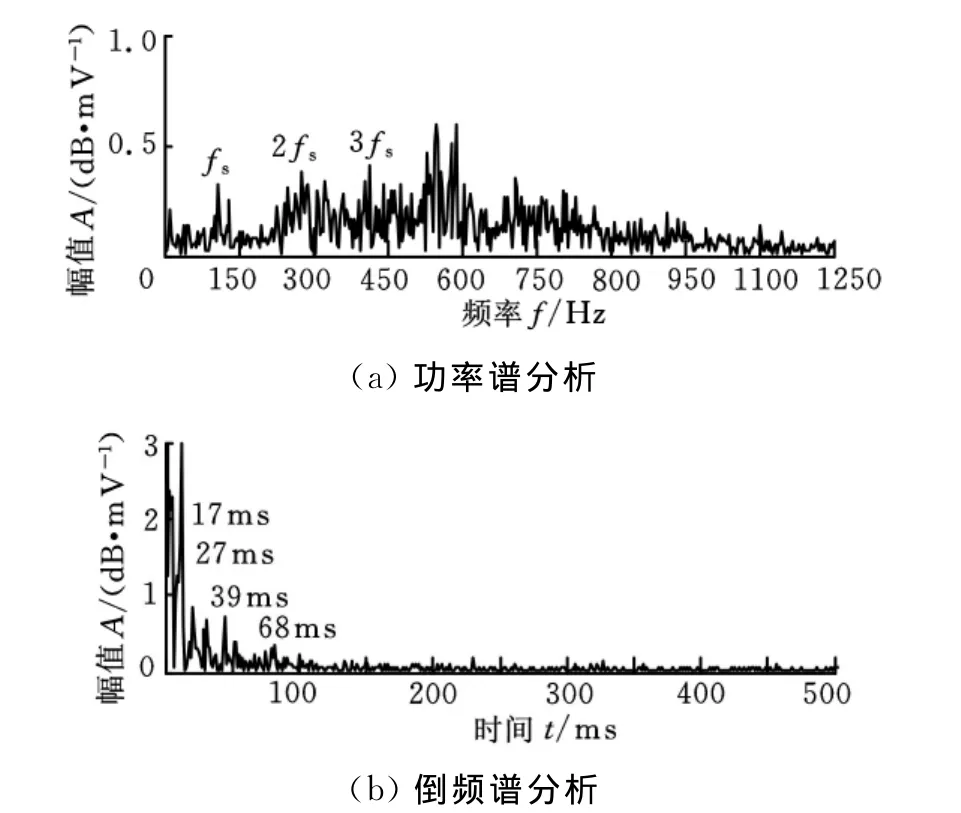
图9 原信号功率谱和倒频谱图
4 结论
(1)根据最小圈数原理可知行星齿轮传动规律,并可根据现有公式和理论进行行星齿轮各个参数的计算。
(2)时域同步平均方法结合加窗原理可在一定程度上抑制能量泄露,保留较好的行星齿轮振动信号。
(3)实验结果验证了时域同步平均的有效性,通过叠加、平均能消除多余噪声和无关分量,获得较完整的行星齿振动信号。
[1]Dong M,He D,Banerjee P,et al.Equipment Health Diagnosis and Prognosis Using Hidden Semimarkov Models[J].Int.J.Adv.Manuf.Technol.,2006,30:738-749.
[2]Samuel P D,Pines D J.Classifying Helicopter Gearbox Faults Using a Normalized Energy Metric[J].Smart Material and Structures,2001,10:145-153.
[3]Blunt D M.Synchronous Averaging Epicyclic Sun Gear Vibration:US,6898975B2[P].2005-05-31.
[4]丁康,李巍华,朱小勇,等.齿轮及齿轮箱故障诊断实用技术[M].北京:机械工业出版社,2005.
[5]McNames J.Fourier Series Analysis of Epicyclic Gearbox Vibration[J].Journal of Vibration and Acoustics,2002,124:150-153.
[6]Samuel P D,Conroy J K,Pines D J.Planetary Transmission Diagnostics[R].Mary Land:NASA Glenn Research Centre,2004.
[7]Smith M R.Internal Vibration Monitoring of A P Lanetary Gearbox[D].Pretoria:University of Pretoria,2009.
