基于微型遗传算法实现特定轨迹和姿态要求的新型机构设计及优化

刘桂萍 薛青青

湖南大学汽车车身先进设计制造国家重点实验室，长沙，410082

0 引言

在轻工、纺织等自动化机械生产中，复杂的生产工艺往往要求机构执行端实现某些特定的轨迹和姿态要求。同时随着生产速度的不断提高，还要求机构的执行端具有良好的运动特性，从而避免对产品造成损伤，保证产品生产质量。执行端可以实现特定轨迹的传统机构主要包括平面四杆机构和类四杆五杆机构，这些机构结构上较为简单，但其执行端很难精确实现给定轨迹，一般也无法满足特定的姿态要求［1］。针对传统机构轨迹综合的局限性，一些学者对混合驱动可控机构进行了研究，较为常见的是混合驱动的五杆机构和混合驱动的六杆机构［2－3］，相比传统单一机构，此类机构具有可控性、可调性，可以精确地实现给定轨迹，但其机构中的伺服电机转向需反复变化，并且杆件的尺寸也需满足连续运转条件，约束太多，不易进行尺度综合。针对这种情况，一些学者开始对凸轮连杆机构、齿轮连杆机构和齿轮凸轮等组合机构进行研究。Mundo等［4－5］先后对凸轮连杆机构和带有非圆齿轮的五杆机构进行了研究，并针对特定的轨迹对机构进行了优化设计；黄德良等［6］也对凸轮连杆机构进行了研究，并且提出了一种双凸轮驱动的五杆机构，该机构利用凸轮驱动代替电机驱动，实现了有速度要求的轨迹设计；隋鹏举等［7］将凸轮连杆组合机构的分析方法运用到齿轮凸轮组合机构中，实现了齿轮凸轮组合机构凸轮廓线的反求设计。目前，大多数学者都把研究重点放在了机构轨迹综合上，很少去关注机构执行端的姿态要求，而在相当一部分实际生产中，不仅要求机构执行端能实现特定的轨迹要求，还要求执行端在运动过程中能保持一定的姿态。

本文首先将机构执行端实现特定轨迹和姿态要求同时进行考虑，设计了一种新型齿轮凸轮组合机构，该机构主要由齿轮机构和凸轮机构构成，可以实现执行端特定的轨迹和姿态要求。然后基于微型遗传算法，提出了一种通过对凸轮廓线进行优化来实现执行端特定的轨迹和姿态要求并提高机构运动性能的设计方法。最后将该新型机构设计方法应用于超高速烟草包装机中，设计了铝箔烟包折叠推手机构。同时以机构执行端的加速度为优化目标，以机构相应的结构参数为设计变量，以最大压力角、最小曲率半径及从动件最大行程等作为约束条件，采用微型遗传算法对新机构进行了优化，进一步提高了该机构在高速条件下的运动性能和包装质量。

1 实现特定轨迹和姿态要求的新型机构设计

为了实现自动化生产机械中执行端复杂的轨迹和姿态要求，本文采用复合运动的设计思想，将执行端的轨迹分解到水平和竖直两个方向分别进行设计。在水平方向上，采用水平直线往复运动机构实现新机构的绝对运动；在竖直方向上，采用导轨、凸轮和一个齿轮来实现机构的相对运动，通过绝对运动和相对运动的复合，机构执行端即可实现特定的轨迹和姿态要求。本文选择两组完全相同的外摆线齿轮组直线运动机构来实现机构的绝对运动，用凸轮机构、导轨及齿轮来实现机构的相对运动，如图1所示。作为一种齿轮凸轮机构，图1所示的新型机构兼有齿轮和凸轮的优良特性，结构紧凑，控制准确有效，可以输出复杂的运动轨迹，并且可以实现某些特定的姿态，例如机构执行端的水平推进和折叠等。

1.1 特定轨迹的实现

新型机构执行端产生的轨迹可看成是由水平和竖直两个方向的轨迹复合而成的。在水平方向上，新型机构采用了两组完全相同的外摆线齿轮组直线运动机构。外摆线齿轮组直线运动机构具有如下特性：①太阳轮的直径为行星齿轮直径的两倍；②齿轮传动杆的长度等于直线运动臂长度。当其结构尺寸满足①、②两个条件时，直线运动臂下端点P便可以始终做直线往复运动。此时，P点满足运动性能良好的简谐运动规律：

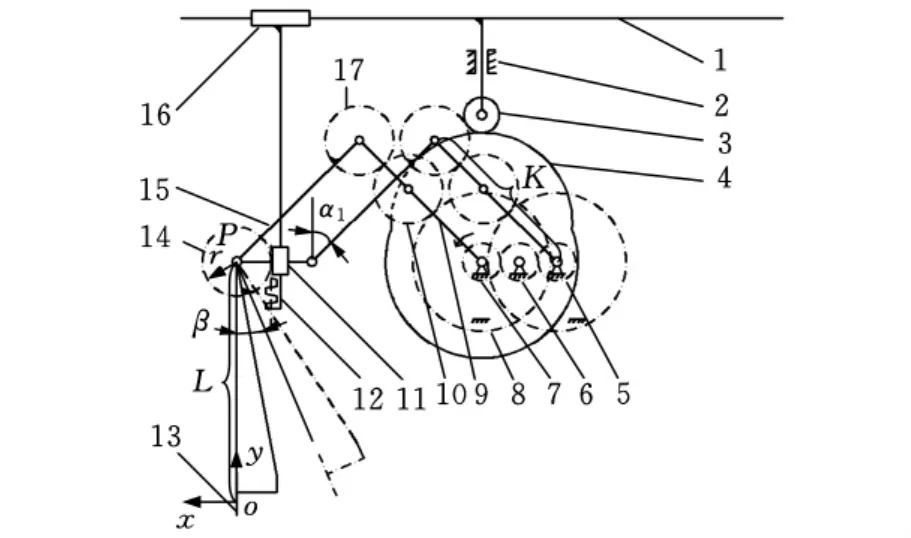
图1 新型机构运动简图

式中，K为行星齿轮与太阳轮的中心距；α1为直线运动臂与竖直方向的夹角（图1）。

在竖直方向上，机构执行端的运动由凸轮机构控制，凸轮控制从动件竖直方向的运动并通过水平导轨和一个齿轮齿条机构传递给机构执行端，这样就将凸轮从动件竖直方向的直线运动转化为执行端的转动，从而可以通过控制凸轮形状来实现执行端的抬升和下降，实现某些复杂的轨迹并满足一些特定的姿态要求。

在轨迹生成中，外摆线齿轮组直线运动机构主要起轨迹行程控制的作用；凸轮机构则主要起调节轨迹形状和运动姿态、改变机构运动特性的作用，是针对不同生产要求进行机构优化设计的主要对象。凸轮从动件的运动规律可以表示为：h＝h（θ），其中，h为凸轮从动件的位移，θ为凸轮工作段转角。下面对新机构轨迹上任意点（x，y）与外摆线齿轮组直线运动机构和凸轮机构的关系进行分析。

建立图1所示的坐标系，其中，坐标原点o为新机构执行端初始状态时对应的设计轨迹上的一点，x轴和y轴分别为执行端水平和竖直方向的位移，点（x，y）为执行端生成的轨迹上某点的坐标，由机构的运动原理可得

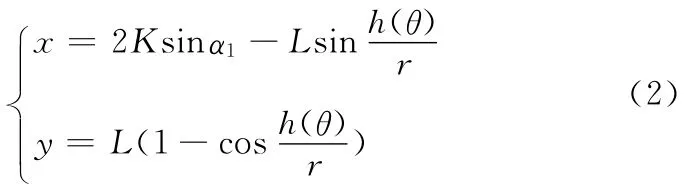
式中，L为机构执行端长度（图1中oP之间的距离），即机构执行端轨迹产生点至执行端固接齿轮中心的距离；r为执行端固接齿轮的半径。

1.2 特定姿态的实现

新机构姿态的实现主要由凸轮机构控制，凸轮通过控制执行端固接齿轮的旋转状态，使得机构执行端完成水平推送、折叠以及避让等一系列姿态。

机构执行端的姿态可以通过执行端固接齿轮的旋转角度β来描述，β与凸轮从动件的运动规律h（θ）有如下关系：

当h′（θ）＝0，即h（θ）＝C为一定值时，执行端固接齿轮的旋转角度β也随之保持不变，在外摆线齿轮组直线运动机构的带动下，执行端将保持一定的姿态运行。特别是当C＝0，即当滚子在凸轮基圆上运动时，执行端可以保持水平姿态沿直线运行。

当h′（θ）＞0时，凸轮从动件处于升程阶段，齿条便会带动执行端固接齿轮逆时针旋转一个角度，使得执行端完成回程避让动作，其抬升量y的表达式为

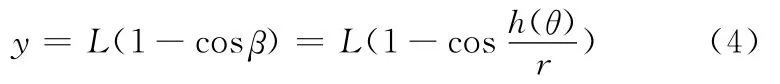
当h′（θ）＜0时，凸轮从动件处于回程阶段，齿条将带动执行端固接齿轮顺时针旋转一个角度，使得机构执行端完成折叠动作，其下降量也可由式（4）确定。

1.3 实现特定轨迹和姿态要求的设计及优化方法

在整个新机构设计过程中，首先需要根据实际生产过程确定机构执行端的轨迹和姿态要求，这其中包括实际生产过程中机构执行端水平直线往复运动的行程要求L1及机构竖直方向的抬升和下降高度要求y。

对于机构执行端轨迹中的直线往复运动和姿态保持段，由机构执行端的直线往复运动行程要求L1即可确定新机构外摆线齿轮组直线运动机构的关键参数K，其中K＝0.25L1，然后根据外摆线齿轮组直线运动机构的结构特点①、②即可确定新机构中各齿轮的相关参数；对于此段轨迹中执行端姿态的保持，凸轮设计时可取h（θ）＝C为一定值，特殊地当C＝0时，滚子位于凸轮基圆位置。

对于机构执行端轨迹的上升段和下降段，机构执行端分别实现避让及折叠姿态。通过式（2），可实现执行端轨迹抬升段和下降段的设计；由式（4）可知，当执行端最大抬升量ymax一定时，可以通过对执行端长度L的设计来控制执行端的最大摆动角度βmax。对于执行端抬升和下降过程中没有严格高度要求的机构设计，可以由式（2）仅通过对凸轮从动件最大行程hmax和特殊控制点处凸轮从动件的行程h（θ1）的设计来满足机构执行端最大抬升高度ymax和控制点处抬升高度的设计要求，并且可以通过对h（θ）进行优化来实现对机构执行端运动性能的优化。

2 基于微型遗传算法的新型机构优化

完成机构的初始设计之后，为了进一步提高机构的运动性能，可对新机构的结构参数进行优化，其优化问题可描述如下：

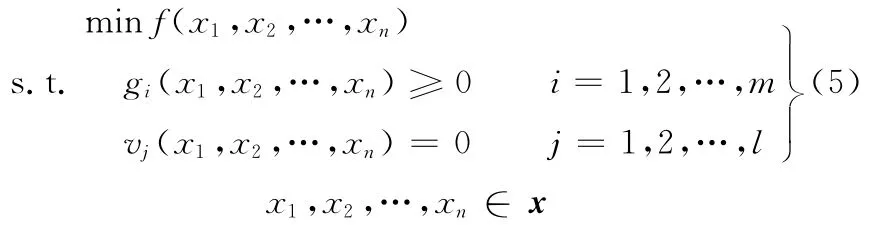
式中，f为优化目标，为保证机构具有良好的运动性能，可选择执行端的加速度等参数作为优化目标；xt（t＝1，2，…，n）为设计变量，可选择影响机构性能的一些结构参数，例如在新设计的机构中影响执行端运动特性的主要为凸轮，所以设计变量可选择控制凸轮从动件运动规律的一些参数；gi和vj分别为设计变量需满足的不等式约束和等式约束，如凸轮廓线要满足最大压力角和最小曲率半径等约束；n为设计变量的个数；x为设计变量的搜索域，可根据实际情况进行确定。

本文选择微型遗传算法作为优化算法，通过对设计变量进行选择、交叉和变异操作，不断寻求适应度更高的个体，在保证轨迹和姿态要求的前提下，完成对新机构的优化。相比于传统遗传算法，微型遗传算法［8］可以有效避免早熟现象的出现，较快地收敛于最优值附近，在处理一些较复杂的优化问题时能够获得更好的优化结果，机构的整个优化流程如图2所示。

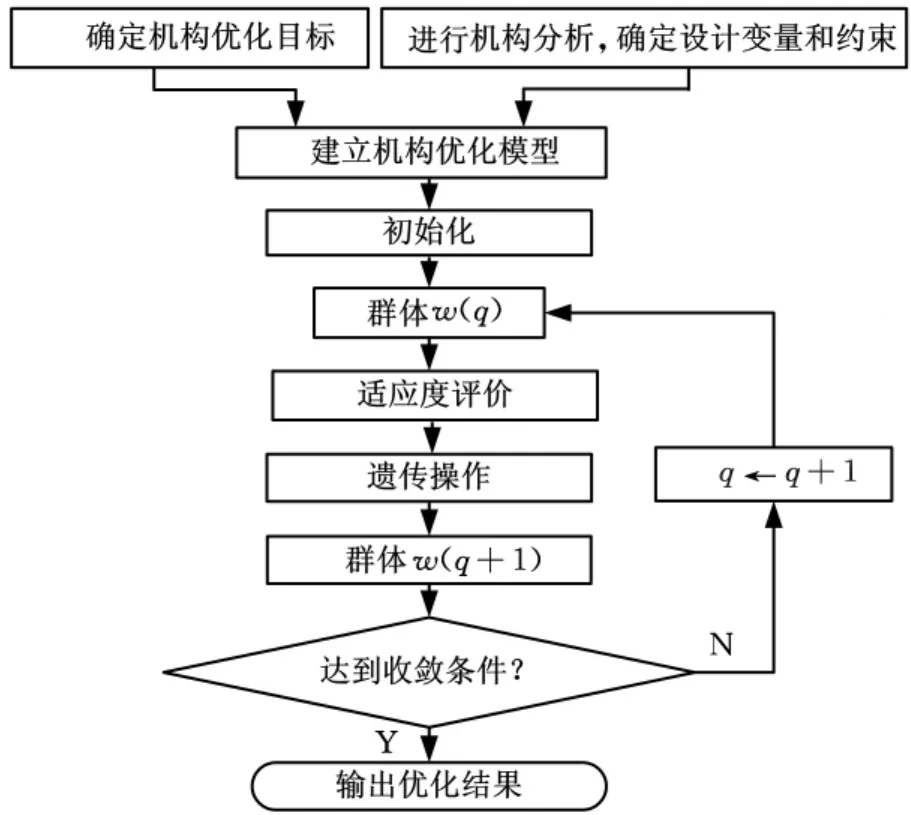
图2 机构优化流程图

3 工程实例

在烟草包装机械中要求设计一种超高速铝箔烟包折叠推手机构。为了保证铝箔烟包推送时的平稳性，提高烟包的包装质量和包装效率，要求超高速铝箔烟包折叠推手机构执行端能够实现对烟包的折叠、水平直线推送和回程避让动作。

3.1 机构的初始设计

为满足烟包的包装要求，铝箔烟包包装推手机构执行端产生的轨迹应具有折叠弧段、直线推送段以及回程避让段，其轨迹可设计为图3所示的形状。确定轨迹形状和姿态等设计要求后，可以根据式（1）和式（2）确定所需的机构结构参数h（θ）和K。设计时根据烟包的尺寸，可选取机构执行端直线往复距离L1＝180mm，由式（1）可得K＝45mm；由外摆线齿轮组直线运动机构的特点①、②，将太阳轮、惰轮和行星齿轮的齿数分别设计为18、9、9，模数统一取为2；取机构执行端最大抬升高度为45mm，最大摆角为60°，执行端固接齿轮模数为2，齿数为12，由式（2）和式（4），将机构执行端长度设计为L＝90mm，凸轮从动件最大行程设计为hmax＝13mm。

对于新机构执行端的姿态设计，一方面，为保证机构执行端直线推烟段的水平姿态，凸轮机构在直线推烟段不应起轨迹调节作用，此时机构执行端满足运动性能良好的简谐运动规律；另一方面，为了实现执行端对烟包的回程避让和折叠动作，保证较好的机构运动特性，需要对凸轮的升程和回程段进行设计，本文采用单停留修正梯形ferguson凸轮曲线对凸轮进行设计，推程角和回程角均设计为90°，近休止角和远休止角分别设计为180°和0°，凸轮实际廓线基圆半径rb取为29mm。

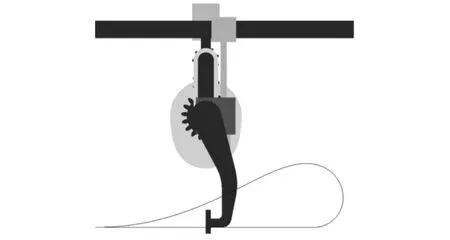
图3 铝箔烟包包装推手机构轨迹设计

3.2 机构优化

由超高速铝箔烟包折叠推手的设计分析可知：一方面，凸轮机构在执行端直线推烟段不应具有轨迹调节作用，此时执行端满足运动性能良好的简谐运动规律，在此段其运动特性不能也不必进行优化；另一方面，铝箔烟包在包装前要完成对烟包的折叠动作，铝箔烟包的包装实际上是从执行端进入直线推烟段前的某弧段开始的。如果机构执行端在折叠弧段水平推烟方向的加速度过大，也会严重影响包装质量，因此，有必要对烟包折叠弧段的凸轮从动件运动规律进行优化，从而达到改善机构执行端运动特性、减小烟包损坏、提高包装质量的目的。

3.2.1 优化设计模型的建立

对于含有凸轮的高速机构的优化［9－10］，凸轮从动件的运动规律可以选用高次多项式表示。本文取凸轮工作段从动件运动规律为7次多项式，其表达式为

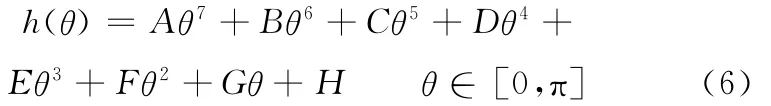
为避免机构高速运行下产生冲击，保证良好的动力学性能，要求凸轮从动件运动始末的位移、速度和加速度为零且加速度在运动过程中没有突变；为保证执行端轨迹高度在一定范围内，要求凸轮从动件的最大行程hmax应在一定的范围内；为保证机构执行端回程时可以对下组烟包进行有效避让，凸轮从动件的运动规律应满足一定的抬升量要求；为提高凸轮机构的工作效率，应增大凸轮对升程过程中的从动件的有效推力，并使凸轮机构的最大压力角不超过规定的许用值；为保证凸轮实际廓线不出现尖点或交叉，避免廓线失真、机构磨损，凸轮廓线的最小曲率半径应不小于一许用值。综上所述，凸轮从动件的运动规律须满足以下10个约束条件：

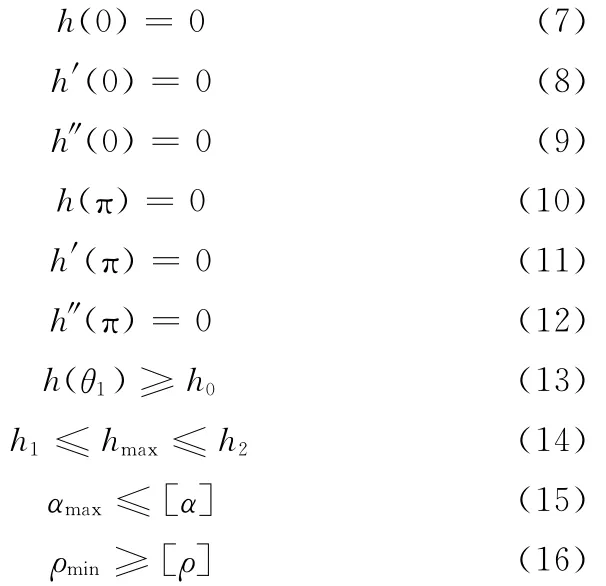
由式（6）可知：h（θ）共有8个自变量，其中有6个等式约束，可取D、E为自由变量，将式（7）～式（12）代入式（6）可解得

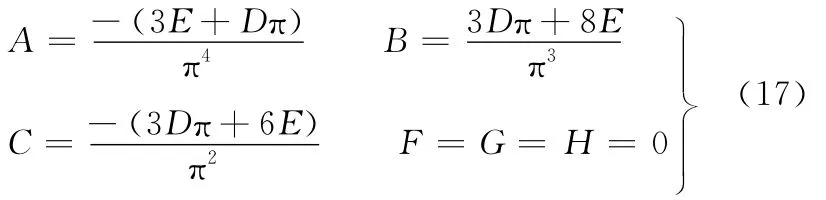
则凸轮从动件的运动规律式（6）可以表示为

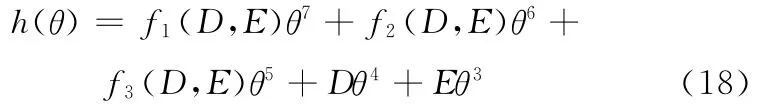
下面分别对约束式（13）～ 式（16）中的参数进行确定：

（1）确定式（13）中的参数h0和θ1。为保证执行端回程时对下组烟包进行有效避让，可取执行端直线段轨迹中点上方对应的轨迹上的一点为回程避让控制点，其对应的凸轮从动件的抬升量为

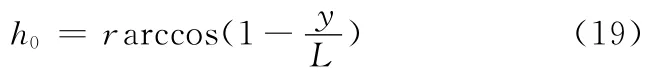
其中，y为回程避让控制点处机构执行端的抬升量，设计时可取y＝15mm。由式（19）可得h0≈7mm。θ1为回程避让控制点对应的凸轮工作段转角，θ1∈［0，0.5π］。由于回程避让点的x坐标值为0，由式（2）可得其对应的α1≈0.814π，同时机构在回程避让段满足α1－θ＝0.5π，可得回程避让控制点对应的凸轮转角θ1≈0.314π。

（2）确定式（14）中的参数h1和h2。为保证机构执行端的抬升量在一定范围内，可以通过对凸轮从动件的最大位移进行限制来实现，对于本文案例，式（14）中的h1和h2分别取9mm和18mm，即可满足要求。

（3）确定式（15）中的许用压力角［α］［11］。机构采用对心直动从动件凸轮，由文献［11］可取凸轮的许用压力角为［α］＝30°。

（4）确定式（16）中的许用最小曲率半径［ρ］［11］。设计时滚子半径r1为6mm，由文献［11］可取凸轮的许用最小曲率半径［ρ］＝12mm。

新机构中凸轮上任一点的压力角α和曲率半径ρ的大小可由下式确定［11］：

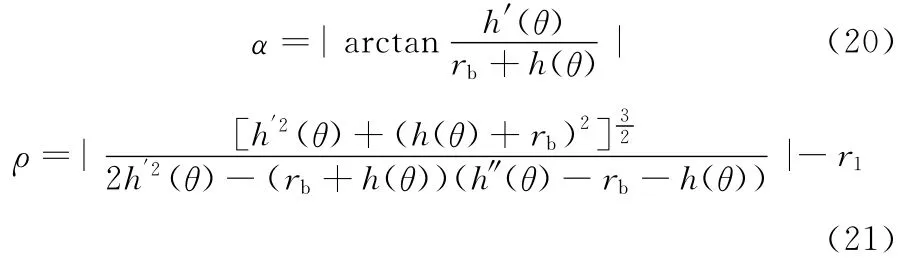
当执行端水平方向推送烟包的加速度过大时，铝箔烟包就会受到较大的惯性力，从而影响包装质量，所以优化时目标函数可以选择机构执行端水平方向的加速度，新机构优化问题可描述如下：

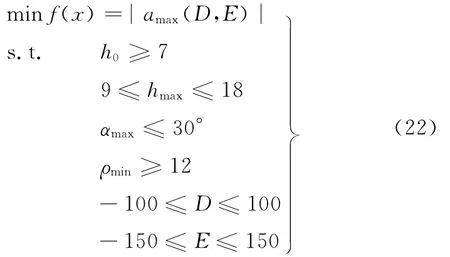
3.2.2 优化结果分析

机构转速为500r/min，微型遗传算法种群大小为5，交叉概率为0.6，变异概率为0.02，利用微型遗传算法通过325次迭代后得到的设计变量的最优解分别为

其对应的目标值为－422m/s2，此时多项式系数A、B、C分别为

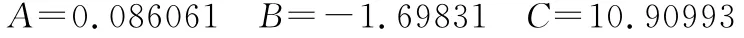
机构优化前后执行端轨迹上各点加速度变化如图4所示。

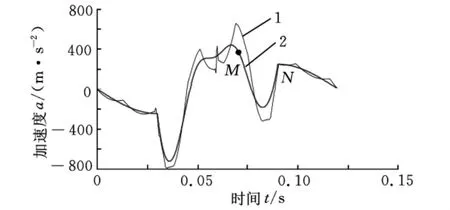
图4 优化前后执行端水平方向的加速度曲线

由图4可以看出：优化后折叠轨迹段MN加速度曲线连续变化且加速度最大值明显下降，从而可以减小执行端对烟包的损坏，达到提高包装质量的目的；与此同时，整个回程避让段加速度曲线更加光滑，最大加速度也有所下降，运动性能得到改善。

4 结束语

本文设计的新型齿轮凸轮机构由齿轮组机构、凸轮机构及导轨构成，其机构执行端可以实现给定的平面轨迹和一些特定的姿态要求，在轻工、纺织、包装等行业具有较高的应用价值；利用优化性能良好的微型遗传算法对机构进行优化后，机构执行端的运动性能可得到进一步提高，通过对烟草超高速包装机械中铝箔烟包折叠推手的设计及优化验证了本文设计方法的可行性。

［1］王成志，陈扼西，纪跃波.平面四杆机构的定性和定位轨迹综合［J］.中国机械工程，2002，14（19）：1623－1627.

Wang Chengzhi，Chen Exi，Ji Yuebo.The Qualitative and Positioning Path Synthesis of Four－bar Linkage［J］.China Mechanical Engineering，2002，14（19）：1623－1627.

［2］周双林.实现轨迹的混合驱动五杆机构设计理论及其实验研究［D］.上海：上海交通大学，2001.

［3］王汝慧，李瑞琴.混合驱动六杆机构的轨迹特性及优化设计［J］.机械设计与研究，2009，25（4）：40－43.

Wang Ruhui，Li Ruiqin.Path Properties and Optimal Design of Hybrid－driven Six－bar Mechanism［J］.Machine Design and Research，2009，25（4）：40－43.

［4］Mundo D，Gatti G，Dooner D B.Optimized Five－bar Linkages with Non－circular Gears for Exect Path Generation［J］.Mechanism and Machine Theory，2009，44：751－760.

［5］Mundo D，Liu J Y，Yan H S.Optimal Synthesis of Cam－linkage Mechanism for Precise Path Generation［J］.Journal of Mechanical Design，2006，128：1253－1260.

［6］黄德良，任子文，史志芳.实现有速度要求轨迹的凸轮连杆组合机构设计［J］.机械设计与研究，2007，23（4）：32－34.

Huang Deliang，Ren Ziwen，Shi Zhifang.Design of the Cam－linkage Composite－mechanism Realizing Trajectory with Velocity Claim［J］.Machine Design and Research，2007，23（4）：32－34.

［7］隋鹏举，姚立纲，苏同克，等.给定运动轨迹的齿轮－凸轮组合机构解析法设计［J］.机械设计与研究，2009，25（5）：10－12.

Sui Pengju，Yao Ligang，Su Tongke，et al.Analytical Design of the Gear－cam Combined Mechanism with the Given Movement［J］.Machine Design and Research，2009，25（5）：10－12.

［8］Goldberg D E.Genetic Algorihms in Search，Optimization and Machine Learning［M］.Canada：Addison－Wesley Publishing Company，1989：148－217.

［9］Alander J T，Lampinen J.Shape Design and Optimization of A Diesel Fuel Injection Cam by Genetic Algorrithm［R］.Vaasa（Finland）：Alander J T，1996.

［10］易传云，钟瑞龄，曹祥敖，等.具有急回特性的插齿主运动机构优化［J］.中国机械工程，2008，19（20）：1184－1187.

Yi Chuanyun，Zhong Ruiling，Cao Xiangao.Optimization for Main Drive Mechanism of Gear Shaper with Quick－return Characteristics［J］.China Mechanical Engineering，2008，19（20）：1184－1187.

［11］石永刚，吴央芳.凸轮机构设计与应用创新［M］.北京：机械工业出版社，2007.