Study on Random Initiation Phenomenon for Sympathetic Detonation of Explosive

Lng CHEN*,Chen WANGChng-gen FENGFeng LUJin-ying LUb, Xio-feng WANG,Xin GUO

Study on Random Initiation Phenomenon for Sympathetic Detonation of Explosive

Lang CHENa,*,Chen WANGa,Chang-gen FENGa,Feng LUa,Jian-ying LUa,b, Xiao-feng WANGc,Xin GUOc

aState Key Laboratory of Explosion Science and Technology,Beijing Institute of Technology,Beijing 100081,ChinabInstitute of Chemical Defense,Beijing 102205,ChinacXi’an Modern Chemistry Research Institute,Xi’an 710065,China

It is important to understand the characteristics of explosive sympathetic detonation for explosive safety.Sympathetic reaction test of GHL (RDX/Al/Binder)explosive charges with shell are conducted.A model of the sympathetic reaction test is established.The elements-apart method and nodes random-failure method are used in the model to describe the expansion progress of shell expanding and the randomly forming process of fragments.Random detonation phenomena of acceptor charge are simulated.

CopyrightⒸ2014,China Ordnance Society.Production and hosting by Elsevier B.V.All rights reserved.

Explosive;Sympathetic detonation;Numerical simulation

1.Introduction

Understanding characteristics of explosive sympathetic detonation is very important to use explosives safely.The charges with and without shells for sympathetic reaction test are used to study the sympathetic action of explosives.In the sympathetic reaction tests of bared explosives,the acceptor is initiated by shock waves or products from donor detonation. Because of shock wave is attenuated rapidly in the air,the critical distance of sympathetic detonation is not longer than the gap of two bared explosive charges.The charges with shells will produce many fragments besides shock wave and detonated products.These fragments may f l y a long distance to impact on the acceptor.The critical distance of sympathetic detonation can be measured in the tests,but detonation details cannot be obtained.Through the numerical simulation of sympathetic reaction tests,the detonation details can be analyzed to help in reducing the number of tests.In 1982, Howe et al.[1]simulated the sympathetic reaction tests with Eulerian code 2DE,calculated the acceptor initiated by shock waves from donor,and analyzed the inf l uence of distance between charges,shell width,board width between donor and acceptor on tests were analyzed.Lu et al.[2,3]calculated the sympathetic reaction tests of PBXN109 explosives without shell in 2006.In 2010,Fisher et al.[4]studied safety of PBXN29 explosive charge with shell in the packaging containers by sympathetic reaction tests and numerical simulations.Shell expanding and impacting acceptor had been considered in calculation,while the distance between donor and acceptor was very close.Because there is a long critical distance for charges with shell in sympathetic reaction test,it is a challenge how to describe shell deformation,fragments forming and fragments action on the acceptor in calculation.

In this paper,the sympathetic reaction tests of GHL(RDX/ Al/binder)explosive charges with shell were conducted to determine critical distance.A model was set up to simulate thesympathetic reaction tests.The elements-apart method and nodes random-failure method were used to describe process of shell expanding and producing fragments randomly.

2.Experiments

The sympathetic reaction test device consists of booster, donor,acceptor and witness plates.Fig.1 is a photo of the sympathetic reaction test.Donor and acceptor were left standing on the ground with some distance apart.The witness plate was set under acceptor.The donor was initiated by a booster.The shock waves,detonation products and shell fragments of the donor acted on the acceptor.The reaction extent of acceptor was assigned based on the damage to the witness plate and the remnants of any un-reacted material.The sympathetic detonation tests were conducted at different distance between donor and acceptor,and the critical distance for acceptor exploding could be found.Here,the charge distance means the shortest distance between charges’boundary of donor and acceptor.The critical distance means the charge distance for sympathetic detonation.

The donor and acceptor were identical cased cylindrical GHL explosive charges.All charges were 60 mm in diameter and 240 mm in length, fi lled in the steel cylinder shells,while the shell was 3 mm in thickness,and its top and bottom covers were 3 mm in thickness and 30 mm in height.The boosters were 25 mm in diameter and 25 mm in length.#The witness plates were 12 mm in thickness and made of 45steel.

Fig.1.Photo of sympathetic detonation test.

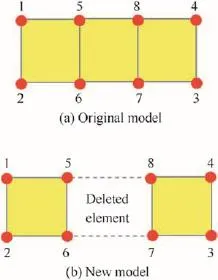
Fig.2.Elements deleted progress in continuous model.

3.Simulation of sympathetic reaction

When the donor blasted,its shell expanded and ruptured to form the irregularly shaped,high-speed fragments with different sizes,and then these fragments acted on the acceptor. If the charge distance from donor to acceptor was long,the actions of shock wave and detonation products were too weak to act on the acceptor,and the acceptor was mainly initiated by these high-speed fragments.The key to simulate the sympathetic reaction was to describe shell deformation,fragment random production and fragments action on the acceptor.In usual calculation,the shell of the donor was developed in continuous model,and some elements were deleted when elements get to its failure values,as seen in Fig.2.The early expansion effect of shell could be simulated,but shell deformation,fragments formation and fragments impacting on acceptor could not be calculated.Herein,the elements-apart method and nodes random-failure method were used in the model to describe the progress of shell expansion and fragment random production.In order to describe the progress of shell fragments,the donor shell was modeled as an accumulation of equal volume elements.The nodes at the same location recomposed to a node group with a failure strain value,as seen in Fig.3(b).If the failure strain value was got, the node group would fail,the adjacent elements would be separated to make the shell rupture and form fragments.The whole process of shell rupture,fragments dispersal and action on acceptor could be simulated.Fig.3(c)showed the failing progress of the node group failed and the formation of the fragments.In practical tests,the donor would produce fragments with different sizes,so the failure strain values were def i ned in random normal distribution.As shown in Fig.3(d), some of node groups got to their failure strain values and the elements separated,while some of them did not.The process of random size fragments forming and fragments action on the acceptor was simulated using the two methods.

Fig.4 shows the randomly forming process of fragments with different sizes.The donor was initiated from the top,and the detonation waves propagated from up to down to make the shell expanding.When the shell expanded at a certain extent, there were breaking holes on the shell formed randomly,and then the holes extended to be fracture belts along the vertical direction,as shown in Fig.4(b).Along with the shell deformation,elements separated and formed fragments,as shown in Fig.4(c).After the donor charge detonated completely,the shell ruptured to form the random size fragments,as shown in Fig.4(d).

Since the failure values of node groups were random,the fragments of donor shell formed random fragments with different size.Even at the same distance between the donor and the acceptor,each calculation could result to different results.This would lead to the random initiation of the acceptor,which was the same as in practical test.Therefore, the multiple calculations at the same distance were required to get the statistical results.In order to reduce computation time and gain more data in each calculation,a four acceptors model was developed.4 acceptors were placed around the donor inthe calculation.There were contacts between fragments of the donor and the acceptors,and no interaction between acceptors. Here we can gain four experiments results in one calculation. Then every calculation equals to 4 parallel tests.Fig.5 shows the positions of the donor and the acceptor,four acceptors took the same distance from the donor.

Because the effects of the shock waves and the products are much smaller than the effect of fragments on acceptors,the air fi eld was not considered in the model,and the propagation of the shock waves in the air was ignored,the description of shell fragments was only focused on.The Lagrangian method was used in the model in order to observe the distortion and the reaction of the acceptors.Fig.6 shows the model of the sympathetic reaction tests,without considering the performance of the detonator,and the initiation point was set in the center of the top surface of donor.

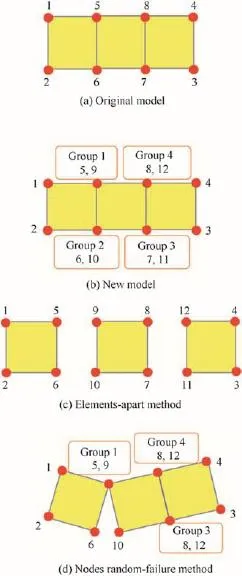
Fig.3.Producing of shell fragments with elements-apart method and nodes random-failure method.

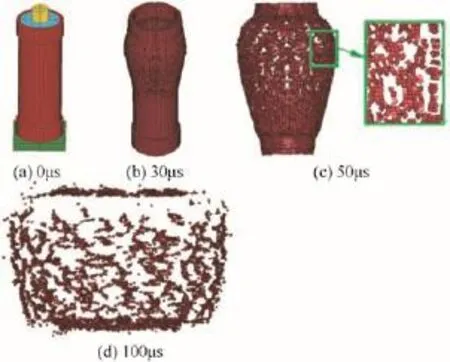
Fig.4.Process of forming random size fragments.

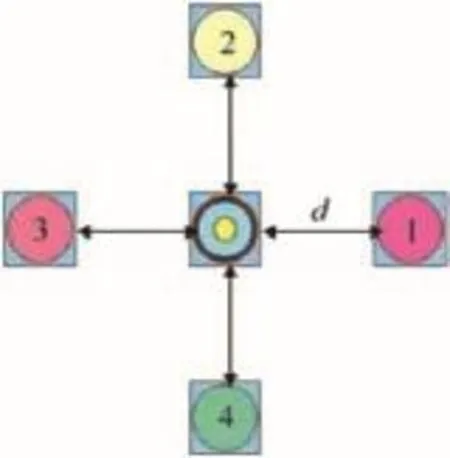
Fig.5.Positions of donor and acceptor.

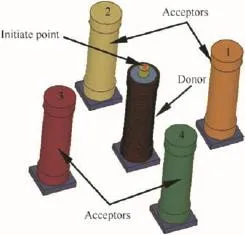
Fig.6.Model of sympathetic detonation test.

The sympathetic detonation tests were simulated by using an explicit f i nite element hydrocode LS-DYNA[5].The elastic plastic hydrodynamic material model was used for the mechanical behaviors of the donor and the acceptors,and the Ignition and Growth reactive(I&G)model[6]was used to describe the GHL explosive detonation.The parameters for Ignition and Growth reactive model for GHL explosives were listed in Table 1[7].

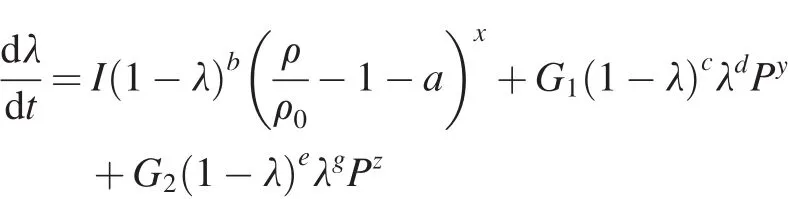
The reaction rate equation in Ignition and Growth model is of the form:where λ is the reacted fraction,t is time,ρ is current density,ρ0is initial density,P is pressure,and I,G1,G2,a,b,x,c,d,y,e,g are constants.

4.Results and discussion

Fig.7 shows the deformation of the witness plate under the acceptor for 225 mm charge distance.It can be seen from Fig.7 that a hole was formed by the acceptor detonation, which was slightly smaller than the diameter of explosive charge.Fig.8 is the photo of acceptor remnants at 273.4 mm charge distance.It can be seen that there were some residual explosives and fragments;the charge was only partial reacted, and did not detonate completely.Fig.9 is the photo of acceptor remnants for 300 mm charge distance.It can be seen from Fig.9 that the lower part of the acceptor charge was destroyed but the upper part was almost intact,a lot of GHL explosives are left in the shell,It meant that the main impaction of the fragments was on the lower part of the acceptor.

The results of tests with different charge distances are listed in Table 2.When the charge distance was less than 150 mm, the acceptors detonated completely;when the distance was in the range from 150 to 300 mm,the acceptors detonate randomly.When the charge distance was exceeds 300 mm, acceptors would not react.The distance from 150 to 300 mm could be considered the critical distance rang.

Fig.7.Witness plate deformation at 225mm charge distance.

Fig.8.Photo of acceptor remnants at 273.4 mm charge distance.

Fig.9.Photo of acceptor remnants at 300 mm charge distance.

Table 1Parameters for Ignition and Growth of reactive model for GHL explosive[7].

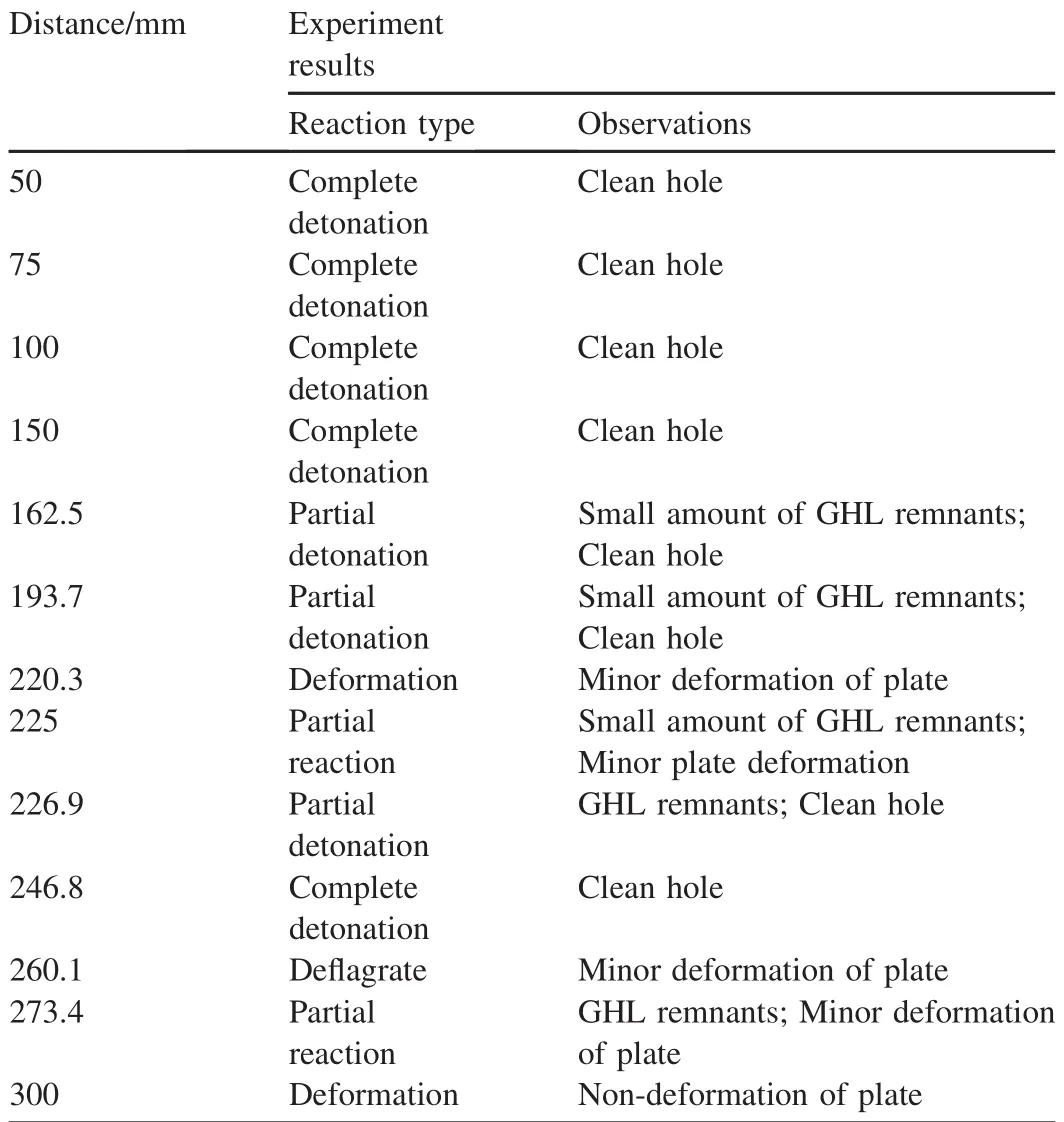
Table 2Tests results of sympathetic reaction.

The simulations of tests at different charge distances were carried out.Table 3 lists the calculated results.The results showed that the distribution of fragments is random,which leads to the random reaction results of acceptors.With the increase in the charge distance,the acceptor detonated easily. The calculated critical distance range is about from 140 mm to 300 mm,which is in agreement with the results of tests mainly.

Fig.10 showed the calculated deformation of the acceptors at different time at 200 mm charge distance.As the donor

exploded, the fragments with different sizes were formed and flied around; some of them impacted the acceptors. At 115 μs, the fragments began to impact Acceptor 1#. Under the impact of fragments, the internal pressure of charges increased, and the detonation waves grew up along the charge. At 165 μs, Acceptor 1# detonated completely, while Acceptor 2# was initiated just now, but Acceptor 3# and Acceptor 4# did not detonate at last.

Table 3Calculated results of sympathetic detonation tests.

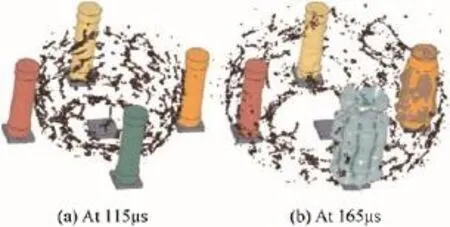
Fig.10.Deformation of acceptors at different time at 200 mm charge distance.

5.Conclusions

The sympathetic reaction tests of GHL explosive charges with shells were conducted.When the donor blasted,its shells would expand and rupture,and formed different sizes,highspeed fragments,and then these fragments f l ied to act on the acceptor,and the acceptor would be randomly initiated by these high-speed fragments.As there was random initiation in sympathetic reaction tests,the key to simulating sympathetic reaction was to describe the random phenomenon.A model was developed for the simulation of sympathetic reaction tests, and the calculated results were compared with the experimental results.The elements-apart method and the nodes random-failure method were used to describe the donor shell. The process of random size fragments formation and fragments action on acceptor was simulated.The random detonation phenomenon of action from donor products to acceptors at different charge distances was simulated.The calculated results are consistent with the experimental results.

[1]Howe PM,Huang YK,Arbuckle AL.A numerical study of detonation propagation between munitions.In:Proceedings of the 7th International Detonation Symposium 1982.pp.1055-61.

[2]Lu JP,Lochert IJ,Kennedy DL,Hamshere BL.Simulation of sympathetic reaction rests for PBXN-109.In:Proceedings of 13th International Detonation Symposium,Norfolk 2006.

[3]Lu JP,Daniel MA,Lochert IJ.Numerical and experimental studies of PBXN-109 sympathetic reaction.In:Proceedings of the 14th International Detonation Symposium,Idaho 2010.pp.11-6.

[4]Fisher S,Baker EL,Wells L,Quigley G,Lew A.XM982 excalibur sympathetic detonation modeling and experimentation.In:Insensitive Munitions&Energetic Materials Technology Symposium,Bristol 2006.

[5]Livemore Software Technology Corporation(LSTC).LS-DYNA users’manual.University of California,Lawrence Livermore National Laboratory;2001.Version 960.

[6]Tarver CM,Hallquist JO,Erickson LM.Modeling of short pulse duration shock initiation of solid explosive.In:Proceedings of 8th International Detonation Symposium,Albuquerque 1985.pp.951-61.

[7]Chen L,Wang C,Lu J-Y,Guo X,Wang X-F.Experiment&simulation of sympathetic detonation tests.Transactions of Beijing Institute of Technology 2009;29(6):497-524.

19 September 2012;revised 4 July 2013;accepted 28 October 2013 Available online 12 December 2013

*Corresponding author.

E-mail address:chenlang@bit.edu.cn(L.CHEN).

Peer review under responsibility of China Ordnance Society

Production and hosting by Elsevier

2214-9147/$-see front matter CopyrightⒸ2014,China Ordnance Society.Production and hosting by Elsevier B.V.All rights reserved.

http://dx.doi.org/10.1016/j.dt.2013.12.002