Rough Sets Probabilistic Data Association Algorithm and its Application in Multi-target Tracking

2013-07-25LongqingNISheshengGAOPengchengFENGKiZHAO

Defence Technology 2013年4期

Long-qing NI*,She-sheng GAOPeng-cheng FENGKi ZHAO

Long-qiang NIa,*,She-sheng GAOa,Peng-cheng FENGa,Kai ZHAOb

aDepartment of Automatic Control,Northwestern Polytechnical University,Xi’an 710072,ChinabNorthwest Institute of Mechanical&Electrical Engineering,Xianyang 721099,China

A rough set probabilistic data association(RS-PDA)algorithm is proposed for reducing the complexity and time consumption of data association and enhancing the accuracy of tracking results in multi-target tracking application.In this new algorithm,the measurements lying in the intersection of two or more validation regions are allocated to the corresponding targets through rough set theory,and the multi-target tracking problem is transformed into a single target tracking after the classif i cation of measurements lying in the intersection region.Several typical multi-target tracking applications are given.The simulation results show that the algorithm can not only reduce the complexity and time consumption but also enhance the accuracy and stability of the tracking results.

Rough set;Target tracking;Data association;Data fusion

1.Introduction

In multi-target tracking(MTT)application,people want to estimate the states of several targets according to the measurements from some kinds of sensors(such as radar,infrared sensor and sonar).If the relationship between a tracked target and measurements lying in the validation regions is known beforehand,the target states could be estimated through standard fi ltering algorithms[1-5](Kalman fi lter,extended Kalman fi lter andsample-based fi lteringmethods).Butinpracticalapplication, this situation may not exist:some of the measurements may be originated from clutter or false alarms(returns from nearby objects like building,water tower,mountain,rain or ECM).So it is the most important to determine the corresponding relationships betweentargetsandmeasurementslyingintheintersectionoftwo or more validation regions in multi-target tracking[6].Two methods can be used to solve the data association problem:a) unique-neighbor data association[7,8],such as global nearest neighbor standard f i lter(GNNSF)and multi-hypothesis tracking (MHT),whichisusedtoassociateallthemeasurements(oroneof themeasurements)withone ofthe previouslycreatedtracks;and b)all-neighbor data association[6,9,10],such as joint probabilistic data association(JPDA),which is used to update all tracks by using all the measurements lying in the validation region. GNNSF only considers the most likely hypothesis for track update and new track initiation so that it is only used for sparse targets,accurate measurements,and low false alarms in the validation region[8,11].The multiple hypothesis tracker(MHT) is recognized theoretically as the optimum approach in Bayesian sense under idealized modeling assumptions.Unfortunately,the computationalcomplexity ofMHT limitsits practicalrealization even using the fastest computers available[9,12].In JPDA,a target tracking is updated by a weighted sum of all the measurements in the validation region[13-15].This means that themeasurements may contribute to the update of more than one target tracks.And also JPDA increases the track variance matrix of Kalman f i lter to account for the association uncertainty,however the increased covariance matrix leads to even more false observations in the validation region[8].In Ref.[9]，a new allneighbor fuzzy association approach is used for tracking multitarget in a clutter environment.This method has a lower computationalcomplexityinaclutterenvironmentattheexpense of a lower performance compared to the standard JPDA.

Inthispaper,theroughsettheoryisusedtodealwiththeecho measurements in the validation regions,and the measurements in the lower approximation,including the measurements originated from target under discussion absolutely，are used to update the target states directly;the measurements,including the measurements which are not originated from target under discussion and may be originated from target under discussion, whichlieintheupperapproximationbutarenotintheboundary region(intersection region)are discarded for target under discussion;the measurements in the boundary region are approximated by the measurements in the lower approximation and upper approximation.In this approach，the measurements in the intersection region are handled discriminatingly,and the validation matrix needs not to be calculated.The approach can eff i ciently reduce the association uncertainty compared with the joint probability data association algorithm.It can reduce the computational complexity to a large degree,and also do not increase the track variance,especially in dense clutter environment.

2.Rough sets and the conformation of decision table for MTT

We assume that there are two targets of interest in the f i led of view(FOV),as shown in Fig.1.In the two validation regions,the measurements y1and,y2may be originated from Target 1 or clutter;the measurementsy5,y6and y7may be originated from Target 2 or clutter;y3and y4may be originated form Target 1,Target 2 or clutter(clutters).

Ifit can be decided that the measurements y3and y4belong to Target 1 or Target 2,the probabilistic data association(PDA) algorithm which can only be used for a single target tracking would be used to deal with the data association in MTT. Unfortunately,the measurements lying in the intersection area are of fuzzy uncertainty forˆy1andˆy2.Fuzzy uncertainty is always associated with a boundary region of a set[16].For example,if an element does not belong to a special set and also doesnotbelongtoits complementary setindomainofdiscourse, it probably belongs to the boundary region of the two sets.The rough set theory[17-22]is a novel mathematics method which can be used to process the uncertain,imprecise and fuzzy informations.This method is based on a classif i cation mechanism, which is considered as equivalence(indiscernibility)relation in the given space.In MTT,the returns lied in the intersection of validation regions can be considered as the boundary elements, and these measurements are uncertain according with the association rule(relationship between targets and measurements).

In the rough set theory,the knowledge is often expressed as information table(information system).The values of elements in the information table are often acquired from sensor or given by expert.In the rough set theory,an information system is denoted as a quadruple[22]:(S=U,A,F,Vd), where U and A are the domain of discussion and the attribute set，respectively,which are the non-empty f i nite sets,F is the maping from set U to set A,and Vdis the value of attribute set. If the attribute set A is decomposed into C and D⊂A,C and D are called conditional attribute and decision attribute, respectively.The information systems are called the decision information systems.The process of data association in MTT is a typical decision information system in which the cumulative set of measurements at time index k can be regarded as the attribute set,and the association relation between target and measurement can be taken as decision attribute,which the measurement associates with which target.measurement,and R(k)is the covariance matrix of measurement error.

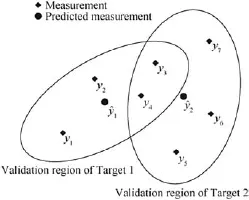
Fig.1.Two targets with common measurements.

Table 1Decision table for Fig.1.

3.Rough sets probabilistic data association(RS-PDA)

Probabilistic data association(PDA)is to use all of the validated measurements with different weights(probabilities) to update the target states[6,10,23].The PDA algorithm is used to calculate the association probability which describes the contribution of each validated measurement to the target of interest in real time.The association probability used in a tracking f i lter accounts for the uncertainty of measurement origin.Since this method does not take into account the measurements in the intersection of two or more validation regions,it can be used only for the tracking of a single target in clutter environment. The association probabilityβi

k,which describes the probability of a measurement origin in PDA,is calculated as follows.Assume that θikis the association event which expresses whether the i-th measurement is associated with a target at time k,Ykis the set of validated measurements at time k,Ykis the cumulative set of measurements at time k,mkis the number of the validated measurements at time k,Vkis the volume of validation region,PGis the gate probability of that the correct measurement falls in the validation region,and PDis the detection probability of that the true measurement is detected. The association probability is calculated as follows[23]

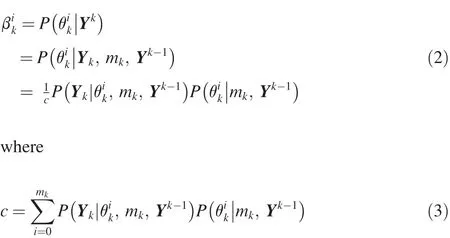
It can be known from the calculation process that the association probability is related with the volume of validation region,number of validated measurements,gate probability, detection probability,distribution function of false measurements and measurement residuals.In multi-target tracking,the calculation of association probabilities is quite complicated because a measurement can be originated from more than one target(for example,the measurements lie in the intersection region).Therefore,the probabilistic data association f i lter (PDAF)is not suitable for multi-target tracking problem unless it can be determined which measurements in the intersection region are originated from which target.

The rough set theory proposed by Pawlak,which is used to deal with the imprecise and uncertain information system with potential knowledge of the information system,is discussed. In the theory,the knowledge is processed and found using equivalence relation or granularity.The equivalence relation and granularity are expressed by two def i nable or observable subsets called lower and upper approximations.The rough set theory has been successfully applied to machine learning, intelligent system,inductive reasoning,pattern recognition, image processing,signal analysis,knowledge discovery,decision analysis,expert system and many other f i elds.In the rough set theory,no prior information beyond the information system to be discussed is needed to accomplish the inference compared with other theory.In multi-target tracking,the measurements lying in the intersection region are uncertain for association application,which makes PDAF unsuitable for MTT.The rough sets theory can be used to deal with the measurements inside the intersection region and approximate these measurements with the measurements certainly associated with some target to be discussed.

Two operators are def i ned on set X⊆U,that is

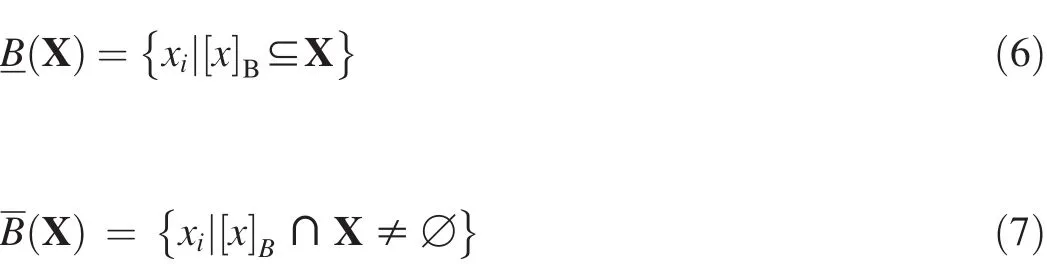
BNB(X)is called the boundary set of X.

For example,two targets at time index k have an intersection validation region,and some measurements lie in the intersection of the two validation regions.According to Fig.1, the lower approximation,upper approximation and boundary region of Target 1 are expressed in Fig.2.

Fig.2.Upper and lower approximations about measurements for validation regions.

In Fig.2,for Target 1,the measurements in the lower approximation are equivalent,these measurements can be used to update the state of Target 1 directly,and the measurements in the upper approximation but not in the boundary region are discarded,and the measurements in the boundary region are indiscernible for Target 1 or Target 2.Therefore,for a given target,only part of the measurements can be used to update the target states.The key of data association is to f i nd out the property of measurements in the boundary region in MTT application(the corresponding relationship between measurements and targets).

The approximation quality of rough sets is expressed as follows[17,22]

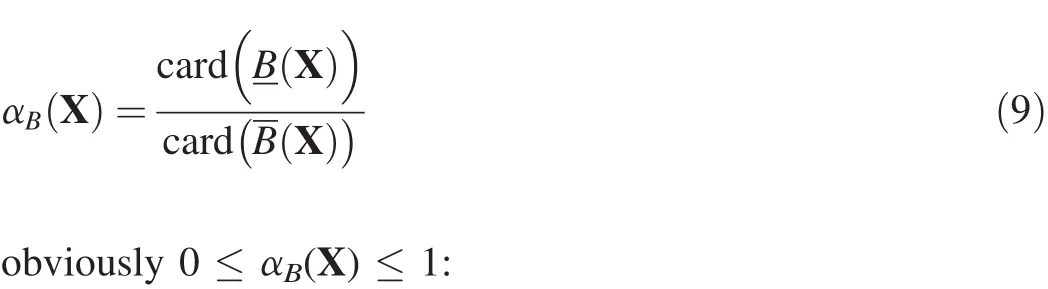
1)If αB(X)=1,then X is crisp with respect to B(X is precise with respect to B).That is to say,the boundary set BNB(X)=0,this indicate that no validation intersection about targets of interest exists in multi-target tracking;

2)If αB(X)＜1,then X is rough with respect to B(X is vague with respect to B).This indicates the intersection regions exist between the target of interest and other targets,and also there are some measurements in the intersection regions;

3)If αB(X)=0,then X is internally B-indef i nable.This means that all the

measurements of target of interest lie in the validation region of other targets.

For 1),the single target tracking and data association approach can be used for multi-target tracking;for 2),the association relationship between measurements and targets needs to be found out,and the tracking f i lter and data association approach are used to update the target states,which will be emphatically discussed in this paper;for 3),the group and extended target tracking approaches can be used.

Approximation quality(Eq.(9))can be used to measure the quality of decision on universe U,so it is proper to use this parameter to approximate the measurements in the boundary regionwiththemeasurementsinthelowerapproximation.Inthe data association,all the measurements in the validation region are approximated with the measurements in the lower approximation by approximation quality.Obviously,if the approximationqualityishigh,themeasurementsintheboundaryregion make more contribution to the target of interest;if the approximationqualityislow,themeasurementsintheboundaryregion make less contribution to the target of interest.Therefore,the measurements in the boundary region can be allotted to the related targets according to this contribution factor.

For the targets having intersection validation regions,the approximation quality factors are inversely arranged according to the target number.That is

and the number of boundary region measurements belonging to the associated validation region of target t is After the number of targets associated with related targets is calculated from Eq.(12),the position of the measurements in the boundary region for the target of interest should be determined.To decide this distribution of measurements,here the measurements in the boundary region is considered as a whole,and the relative distance factor is calculated by Eq.(13).

Where，di2（k）is the distance between the predicted measurement and the considered measurement;ei(k)is the measurement residual;dm2ax，i（k）is the maximum distance on the direction of line connecting between the predicted measurement and the considered measurement in the validation region.

For Target t,Nitmeasurements are selected from the boundary regiotn randomly,and the value of the relative distance factor d(k)should be kept constant.After the number and position of the measurements in boundary region are determined,the updated states of target can be calculated as follows[6,10,23]

4.Data simulation and result analysis

where Ft(k)is the state transition matrix,Gt(k)is the noise matrix,and wt(k)is the process noise which is assumed as white and normal probability distributions,that is

where v(k)is the measurement noise,which is assumed as white and normal probability distributions,that is

4.2.Data simulation and analysis

In practical application,most of the target motion is composed of straight line and turning motions,including uniform speed or uniform acceleration,and the relative space relation of multi-target is composed of cross relation,parallel relation and split relation.For straight line moving target,the dynamics of the target is modeled as a linear discrete Wiener velocity model(DWVM):

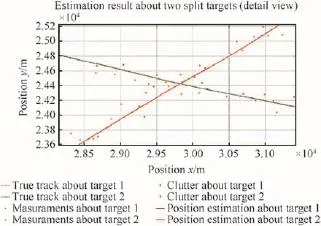
Fig.3.Tracking results of two cross targets simulated with RS-PDAF(detailed view).

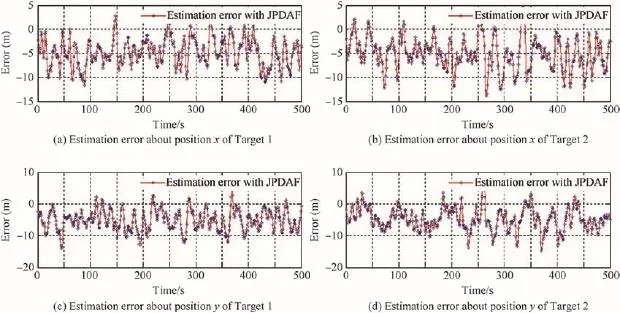
Fig.4.Track errors of two cross targets simulated with RS-PDAF(50 Monte Carlo simulations,and total time consuming:28.326 s).

Fig.5.Tracking errors of two cross targets simulated with JPDAF(50 Monte Carlo simulations,and total time consuming:35.536 s).

Here RS-PDAF is used to track two targets.Fig.3 shows the tracking results of two cross targets,Fig.6 shows the tracking results of two parallel targets,and Fig.9 shows the tracking results of two split targets in clutter environment.In Figs.4,5,7,8,10 and 11,the tracking errors for two cross targets,parallel targets and split targets simulated by RS-PDAF and JPDAF are compared,respectively.Here we assume the sampling interval Δt=1 s,the simulation process lasts for 500 s,the clutter density(expected number of false returns per unit volume in the measurement space)λ=103/km2,the measurement noise covariance matrix R=[9 100],the process noise covariance matrix Q=[16 16].

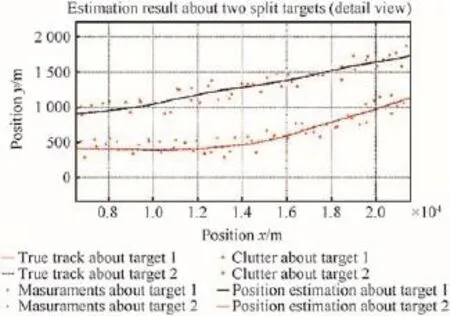
Fig.6.Tracking results of two parallel targets simulated with RS-PDAF (detailed view).

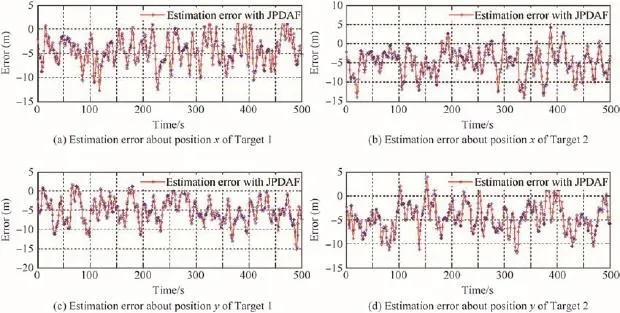
Fig.7.Tracking error of two parallel targets simulated with RS-PDAF(50 Monte Carlo simulations,and total time consuming:27.764 s).

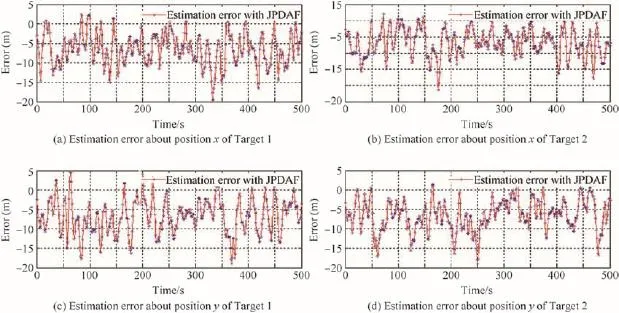
Fig.8.Tracking errors of two parallel targets simulated with JPDAF(50 Monte Carlo simulations,and total time consuming:34.562 s).

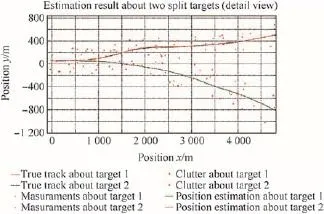
Fig.9.Tracking results of two split targets simulated with RS-PDAF(detailed view).

Figs.3-11 show the simulation results of cross,parallel and split targets based on RS-PDA and JPDAF,respectively. The tracking errors are listed in Table 2,and the time consuming is listed in Table 3.

It can be seen from Tables 2 and 3 that the calculating errors ofRS-PDAarelessthanthoseofJPDA,andthetimeconsuming of RS-PDAF is 20%less than that of JPDAF.This is because JPDA makes an indiscriminate advantage of the measurements lyinginthevalidationregion.Thereforethemeasurementslying in the intersection region may be used for the state update of multiple targets,but RS-PDA distinguishes the measurements lying in the intersection of the validation regions for corresponding targets,compared with JPDAF this reduces the uncertainty about the origination of measurements.Because the RS-PDAF does not have to calculate the validation matrix which is time-consuming while JPDA f i lter does,the time consuming of RS-PDAF is less than that of JPDA f i lter.

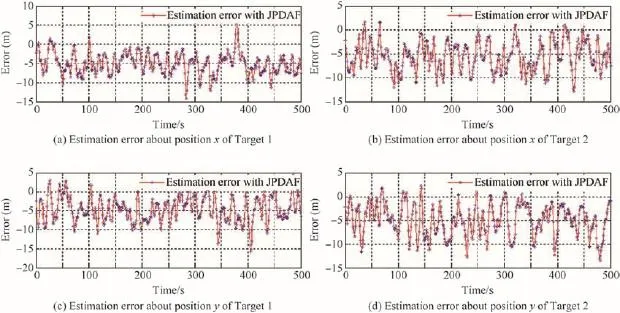
Fig.10.Tracking errors of two split targets simulated with RS-PDAF(50 Monte Carlo simulations,and total time consuming:28.403 s).

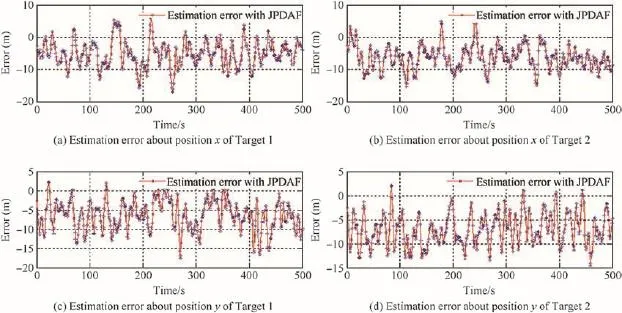
Fig.11.Tracking errors of two split targets simulated with JPDAF(50 Monte Carlo simulations,and total time consuming:32.922 s).

5.Conclusions

Table 2Tracking error comparison between two methods for three cases.

In this paper,a new data association method,RS-PDAF, based on rough sets theory is proposed.The method can reduce the uncertainty of the origination of measurements,and also make advantage of the measurements lying in the intersection region more objectively than JPDAF.After the classif i cation of rough sets,the relation between targets and measurements become clear so that the multi-target problem is easily translated into single target tracking.Compared with JPDAF,RS-PDAF reduces the number of measurements lying in the intersection region for a given target,makes data association process simpler and time-saving,and does not add the variance matrix of Kalman f i lter.Some typical datasimulations are proposed to illustrate the eff i ciency of this novel approach.The simulation results show that RS-PDA is more accurate and less time consuming compared with traditional JPDA.

Table 3Time consuming for 3 cases.

[1]Ristic B,Arulampalam S,Gordon N.Beyond the Kalman fi lter particle fi lters for tracking application.Artech House;2004.

[2]Arulampalam MS,Maskell S,Gordon N.A tutorial on particle fi lters for online nonlinear/non-Gaussian Bayesian tracking.IEEE Trans Signal Process 2002;50(2):174-88.

[3]Kandepu R,Foss B,Imsland L.Applying the unscented Kalman fi lter for nonlinear state estimation.J Proc Contr 2008;18(7):753-68.

[4]Luo X,Moroz IM.Ensemble Kalman fi lter with the unscented transform. Phys D Nonlinear Phenom 2009;238(5):549-62.

[5]Musa ZB,Watada J.Motion tracking using particle fi lter.KES 2008:119-26.Part III,LNAI 5179.

[6]Kirubarajan T,Bar-Shalom Y.Target tracking using probabilistic data association-based techniques with applications to sonar,radar,and EO sensors.In:Handbook of multisensor data fusion:theory and practice. 2ed.CRC Press;2008.

[7]Vasquez JR,Williams JL.Exploiting correlation effects within multiplehypothesis tracking.Math Comp Model 2006;43:1254-66.

[8]Blackman SS.Multiple hypothesis tracking for multiple target tracking. IEEE A&E Mag 2004;19:5-8.

[9]Aziz AM.A novel all-neighbor fuzzy association approach for multitargettrackinginaclutteredenvironment.SignalProcess 2011;91(8):2001-15.

[10]Kirubarajan T,Bar-shalom Y.Probabilistic data association techniques for target tracking in clutter.Proc IEEE 2004;92(3):536-57.

[11]Blackman S,Popoli R.Design and analysis of modern tracking systems. Norwood,MA:Artech House;1999.

[12]Aziz AM.Fuzzy track-to-track association and track fusion approach in distributedmultisensor-multitargetmultiple-attributeenvironment. Signal Process 2007;87(6):1474-92.

[13]Ba HX,Cao L,He XY,Cheng Q.Modi fi ed joint probabilistic data association with classi fi cation-aided for multitarget tracking.J Syst Eng Electr 2008;19:434-9.

[14]Han CZ,Zhu HY,Duan ZS.Multi-source information fusion.Beijing: Tsinghua University Press;2006.

[15]Messaoudi Z,Ouldali A,Oussalah M.Joint multiple target tracking and classi fi cation using controlled based cheap JPDA-multiple model particle fi lter in cluttered environment.In:ICISP 2008.pp.562-9.LNCS 5099.

[16]PawlakZ,SkowronA.Rudimentsofroughsets.InformSci 2007;77(1):3-27.

[17]Pawlak Z.Rough sets and intelligent data analysis.Inform Sci 2002;147:1-12.

[18]Pawlak Z,Grzymala-Busse J,Slowinski R,Ziarko W.Rough sets. Commun ACM 1995;38(11):89-95.

[19]Pawlak Z,Skowron A.Rough sets:some extensions.Inform Sci 2007;177(1):28-40.

[20]Skowron A,Swiniarski R.Rough sets and higher order vagueness.Rough sets,fuzzy sets,data mining,and granular computing.In:10th International Conference,Regina,Canada,3641;2005.pp.33-42.

[21]Yao YY.The superiority of three-way decisions in probabilistic rough set models.Inform Sci 2011;181(6):1080-96.

[22]Zhang WX,Qiu GF,Duan ZS.Uncertain decision making based on rough sets.Beijing:Tsinghua University Press;2005.

[23]Bar-Shalom Y.Tracking and data association.Boston:Academic Press; 1988.

15 May 2013;revised 14 August 2013;accepted 19 August 2013 Available online 6 December 2013

*Corresponding author.

E-mail address:shepherdni@163.com(L.Q.NI).

Peer review under responsibility of China Ordnance Society

Production and hosting by Elsevier

http://dx.doi.org/10.1016/j.dt.2013.11.004

Defence Technology

2013年4期