基于运动目标检测的同步轨道星-空双站SAR杂波特性分析

张丹丹*①②③ 仇晓兰①② 胡东辉①② 丁赤飚①



基于运动目标检测的同步轨道星-空双站SAR杂波特性分析

张丹丹仇晓兰胡东辉丁赤飚

(中国科学院电子学研究所 北京 100190)(中国科学院空间信息处理与应用系统技术重点实验室 北京 100190)(中国科学院大学 北京 100190)

同步轨道星-空双站SAR构型下(卫星作为发射端、浮空器作为接收端)，为了应用空时自适应处理(Space Time Adaptive Processing, STAP)方法更好地抑制杂波，进行地面慢速运动目标检测，有必要分析杂波特性。该文从地面运动目标检测角度出发，建立了同步轨道星-空双站SAR杂波特性的理论模型，分析了杂波的角度-多普勒轨迹的距离依赖性特点，仿真实验证明了模型建立和理论分析的正确性。该文的理论模型和分析结论揭示了同步轨道星-空双SAR这一新模式下的杂波特性，为该模式下地面运动目标检测方法的选择和研究奠定了理论基础。

同步轨道；双站；地面运动目标检测；杂波特性；距离依赖性

1 引言

同步轨道SAR可实现对于重点区域的长时间观测，以浮空器为接收端形成的同步轨道星-空双站SAR抗干扰能力强、安全性高，并且由于浮空器距目标较近，其较同步轨道单站SAR具有更好的信噪比，因此其在军事应用上具有很大优势。地面运动目标指示(Ground Moving Target Indication, GMTI)是同步轨道星-空双站SAR一个十分重要的应用方向，开展该模式下GMTI技术的研究具有重要的实用意义。

杂波特性分析是同步轨道星-空双站SAR- GMTI研究中一个十分重要的环节。杂波的特点，特别是其双站构型下杂波特性的距离依赖性，直接决定了STAP等杂波抑制方法的应用效果。已有的关于双站构型下杂波特性的研究大都是基于机载双站雷达，基于星-空双站杂波特性的研究相对较少，并且，关于同步轨道星-空双站SAR-GMTI的研究大多基于发射端为地球静止轨道的假设。然而同步轨道SAR必然是与地面存在相对运动的，针对这种模式下杂波特性的研究还未有报道。

因此，本文分析了同步轨道星-空双站SAR构型下的杂波特性，从而为该构型下的杂波抑制和运动目标检测奠定了基础。本文结构安排如下：第2节建立了同步轨道星-空双站SAR杂波角度-多普勒轨迹模型，分析了同步轨道星-空双站SAR构型下杂波特性，并在接收空间锥角一定时，推导了多普勒频率相对于双站距离的导数，由此研究了多普勒特性的距离依赖性；第3节通过仿真数据，验证了第2节中推导的公式，并实验验证了上述关于同步轨道星-空双站SAR构型下杂波角度-多普勒轨迹距离依赖性的分析；第4节总结了全文。

2 同步轨道星-空双站SAR杂波特性分析

本节首先建立了同步轨道星-空双站SAR空间几何模型，之后从空间几何模型出发，建立了杂波角度-多普勒轨迹模型，分析了杂波角度-多普勒轨迹模型的距离依赖性。

2.1 同步轨道星-空双站SAR空间几何模型

在分析同步轨道星-空双站SAR杂波特性之前，首先需建立同步轨道星-空双站SAR空间几何模型。本文研究的构型为同步轨道卫星发射、浮空器接收的双站SAR模式，其中发射端为倾斜地球同步轨道卫星(轨道倾角不为)。为便于分析，将同步轨道卫星利用卫星轨道参数进行建模，通过卫星轨道坐标系、卫星平台坐标系、卫星星体坐标系、天线坐标系、不转动地心坐标系、惯性地心坐标系等之间的一系列转换，最后在场景坐标系内对发射端、接收端和场景目标之间的几何关系进行建模。图1为场景坐标系-下同步轨道星-空双站SAR几何构型图，其中为场景中心，指向接收机飞行方向，轴垂直向下，轴遵照右手规则。本文的分析均是在场景坐标系下进行的。

2.2 杂波角度-多普勒轨迹模型

杂波的角度-多普勒轨迹是应用Space Time Adaptive Processing (STAP)等杂波抑制方法的理论依据。本小节从同步轨道星-空双站SAR空间几何模型出发，建立了杂波的角度-多普勒轨迹模型。

图1 同步轨道星-空双站SAR在场景坐标系下的几何构型图

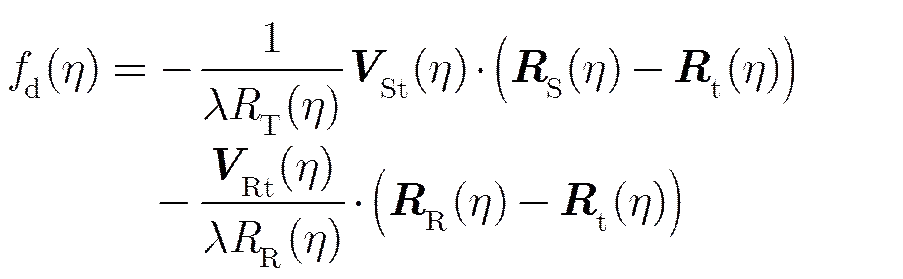
借鉴文献[16]对星载多普勒历程的推导，式(1)可写为

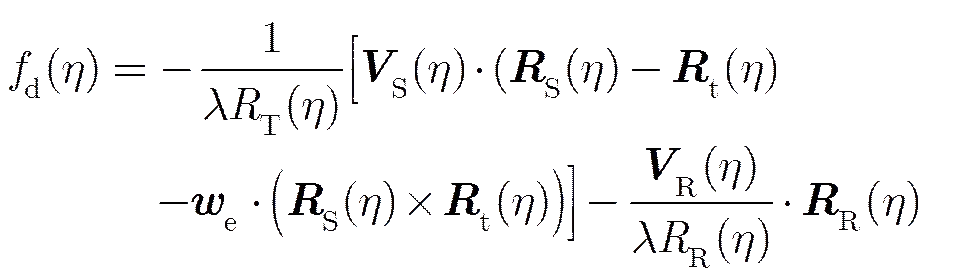
同步轨道卫星作为发射端时，必须考虑地球自转对多普勒频率的影响。可采用多普勒零偏航控制技术来使多普勒中心频率近似为0。

设接收端天线为正侧视接收，将式(1)经坐标转换，可将杂波多普勒频率在场景坐标系下(如图1所示)表示为(此后推导为方便书写，将时间略去)

(4)

在某一时刻，设接收站接收到的来自某距离环信号的双站距离为，该距离环上来自不同空间接收锥角方向的杂波的多普勒频率不同。因此，杂波多普勒频率可表示为接收锥角余弦(表示目标的空间信息)的函数。等距离环上，多普勒频率随接收锥角余弦变化的关系，即为杂波角度-多普勒轨迹。对处于场景中相同位置的杂波点和运动目标(相同)，其多普勒频率不同，因而运动目标并不在杂波的角度-多普勒轨迹上。据此，可以把运动目标和杂波区别并检测出来。

由文献[9-11]可知，机载双站构型下，杂波的角度-多普勒轨迹具有距离依赖性，因而会影响样本协方差矩阵的估计(利用待检测数据的邻近距离门数据作为样本)，进而降低STAP抑制杂波的性能。为考察同步轨道星-空双站构型下，杂波角度-多普勒轨迹的距离依赖性，推导得到该构型下双站等距离线(图1中场景坐标系下)：

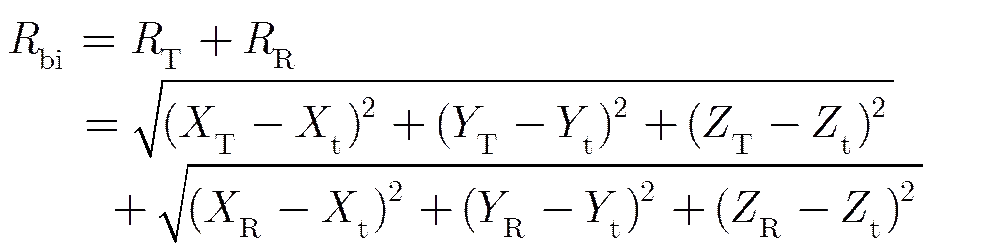
等距离线上的杂波角度-多普勒轨迹，可通过求解式(3)-式(5)组成的方程组得到。由于直接求解方程组的解析式比较困难，可通过数值仿真求解多普勒频率和接收锥角余弦的关系。

下面分析同步轨道星-空双站SAR构型下，杂波角度-多普勒轨迹的距离依赖性。由式(3)可知，双站构型下多普勒频率由两部分组成：由于发射端和目标相对运动产生的多普勒频率(简称为发射多普勒频率)、由于接收端和目标相对运动产生的多普勒频率(简称为接收多普勒频率)。发射等多普勒线和接收等多普勒线是不重合的，因此，对两个不同距离门,分别对应的两条角度-多普勒曲线,，接收机正侧视条件下，接收锥角相同时，接收多普勒频率相同，而发射多普勒频率不同，因而,上相对应的多普勒频率值是不同的。因此，同步轨道星-空双站SAR构型下，杂波角度-多普勒轨迹是距离依赖的。而且，由上述分析可知，杂波角度-多普勒轨迹的距离依赖性是由发射端参数决定的，由于同步轨道卫星参数与机载参数的显著不同，其杂波角度-多普勒轨迹的距离依赖性必然是有差别的。

2.3 杂波角度-多普勒轨迹距离依赖性分析

由上小节分析可知，杂波特性距离依赖性影响STAP杂波抑制的性能，而由于同步轨道卫星参数与机载参数的显著不同，杂波角度-多普勒轨迹的距离依赖性必然是有差别的。本小节分析同步轨道星-空双站构型下杂波角度-多普勒轨迹的距离依赖性。

同步轨道星-空构型下(如图1)，接收端空间锥角一定时，可求得多普勒频率对双站距离的偏导数如下式：

根据上述推导公式，下面讨论同步轨道卫星发射端对杂波角度-多普勒轨迹距离依赖性的影响。设接收端参数不变，观测场景相同，双站角相同，则与高度较低的发射端(如飞机)相比，式(6)中大括号部分可视为变化不大，重点观察式中第2项。第2项中分子为同步轨道卫星等效速度。为使第2项分母部分易于直观理解，设,，则图1中的3维双站几何转化为2维平面结构(如图2所示)。此时，第2项分母部分的物理含义即为发射距离与发射距离在接收距离方向投影的和(图2中大括号所示)。因此，在发射距离和接收距离夹角相同的条件下，越大，则式(6)的值越小，双站杂波角度-多普勒轨迹的距离依赖性越小。对于同步轨道卫星来说，其高度非常高，因而很大(约)，杂波角度-多普勒轨迹的距离依赖性很小。图3为根据式(6)画出的观测场景范围内的多普勒-距离偏导数等高线图。其中，图3(a)的发射端为同步轨道卫星，图3(b)的发射端为飞机(速度为，高度为)，设二者发射的信号相同，接收端参数相同。由图3(a)和图3(b)对比可知，同步轨道卫星作为发射端时，观测场景内等距离线间的多普勒-距离偏导数的值远小于飞机作为发射端时的情况，即同步轨道双站条件下，杂波角度-多普勒轨迹的距离依赖性很小。

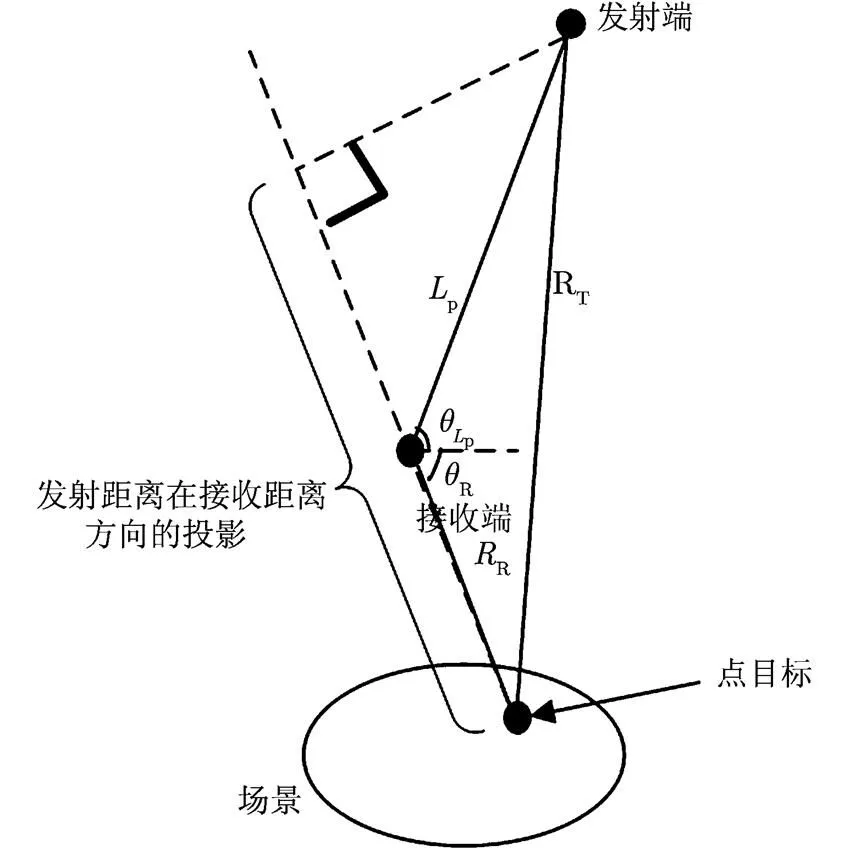
图2 双站2维平面示意图

图3 多普勒-距离偏导数等高线图

Fig. 3 The contour map of Doppler-range partial derivative

另一方面，从物理概念上来说，在接收机正侧视的条件下，引起杂波角度多普勒特性随双站距离变化的根本原因在于，对不同距离门，相同的接收锥角，发射端相对于静止目标运动而产生的多普勒频率不同。对于相同的观测场景，本文研究的构型下，场景到发射端距离(量级，而飞机作为发射端时，场景到发射端距离的典型值为)很大，因而，由于发射端相对于静止目标运动而产生的多普勒频率在整个场景的变化较小，即，杂波角度-多普勒轨迹的距离依赖性较小。

3 仿真实验

为了验证上述同步轨道星-空模式下杂波角度-多普勒轨迹距离依赖性的结论，进行仿真实验。分别对上述杂波角度-多普勒轨迹距离依赖性公式的正确性和上述同步轨道星-空双站SAR角度-多普勒轨迹距离依赖性的分析进行验证。

3.1 杂波角度-多普勒距离依赖性公式正确性验证

由于同步轨道卫星有些参数难以计算，为了用数值说明2.3节式(6)的正确性，利用简化后的同步轨道星-空双站模型(接收端参数为典型浮空器参数，如表1；发射端设为直线飞行，正侧视，参数如表2)计算接收锥角余弦一定时，相距1000个距离门的两条角度-多普勒曲线的多普勒差别，并和利用式(6)的估算值比较，结果见表3。可见，理论估算值和实际仿真值大致相同，其差别远小于一个多普勒分辨单元(PRF为240 Hz，处理脉冲数为40时，多普勒分辨单元为6 Hz)；并且接收锥角余弦一定时，相距1000个距离门(两个距离门间距8.33 m)的两条角度-多普勒曲线的多普勒差别很小，说明距离依赖性较弱。理论估算值和实际仿真值的差别是由于，对两个距离门之间沿特定等接收锥角线的每个点，其多普勒频率对双站距离的偏导数均不相同，对于仿真而言，需要采用一个区域边缘点进行估算，而对于理论估计而言，是针对区域中心目标进行计算的，所以两者本身就会存在微小的差别。

表1 典型浮空器接收端参数

Tab. 1 Typical parameters of the aerostat receiver

表2 等效同步轨道卫星仿真参数

Tab. 2 Simulation parameters of simplified geosynchronous satellite

表3 接收锥角一定时不同距离门多普勒差值

Tab. 3 The difference between Doppler frequencies of two different range gates when the cone angle ofthe receiver is a fixed value

3.2 同步轨道星-空双站SAR杂波特性

本小节通过实验仿真的方法验证上述同步轨道星-空双站构型下杂波角度-多普勒轨迹距离依赖性的结论。接收端参数见表1，发射端参数如表4所示。

首先仿真分析同步轨道星-空双站构型下，影响杂波角度-多普勒轨迹距离依赖性­的因素。双站构型下杂波角度-多普勒轨迹具有距离依赖性，其和等距离线、等多普勒线、等接收锥角余弦线的分布均有关系。图4为等距离线、等多普勒线、等接收锥角线在仿真场景中的分布，其中图4(b)为接收机3 dB波束范围内场景。由图4可知，等接收锥角线和等多普勒线没有完全重合，因而在不同的两条等距离线上，与特定的等接收锥角线相交的两点处于不同的两条等多普勒线上，这说明杂波多普勒特性具有一定的距离依赖性。这是由于双站构型下发射端和接收端分离，若发射端和接收端重合，则等接收锥角线和等多普勒线重合(单站正侧视情况)，此时杂波角度-多普勒轨迹没有距离依赖性。

表4同步轨道卫星仿真参数

Tab. 4 Simulation parameters of geosynchronous satellite

下面仿真同步轨道卫星-浮空器模式下(参数见表1、表4)杂波的角度-多普勒曲线，结果见图5。图5中共仿真了3条杂波-多普勒曲线，相邻两杂波-多普勒曲线所对应的双站距离相差1000个距离门。由于同步轨道星-空双站模式下的方位移变性及距离徙动的影响，一般杂波抑制所需样本数小于1000，故只需考察相距1000个距离门的杂波-多普勒曲线。由图5可见，不同两条杂波角度-多普勒曲线差别很小；并且在本文构型下，当发射机和接收机位于场景的同侧时(图5(a))，杂波特性的距离依赖性更小。这是因为，当发射机和接收机位于待观测场景同侧时(待观测场景为图4(a)中黑框部分)，等接收锥角线和等发射锥角线趋于一致(比较图4(a)和图4(b)可知)，杂波的角度-多普勒轨迹距离依赖性更小。故本文构型设计时，设置了接收机位置(接收机位置见图4(a)处“⊕”处)，使发射机和接收机位于待观测场景同侧，待观测场景位于接收机3 dB波束范围内。图5(b)为位于接收机3 dB波束范围内的角度-多普勒曲线部分，可见，不同角度-多普勒曲线之间差别很小。

最后仿真飞机作为发射端时杂波的角度-多普勒曲线，以与同步轨道卫星作为发射端时杂波的角度-多普勒曲线进行比较。发射端飞机高10 km，与同步轨道双站的双站角相同，发射信号的波长相同。飞机作为发射端时接收机3 dB波束范围内的两条杂波角度-多普勒曲线见图6，两杂波-多普勒曲线所对应的双站距离相差1000个距离门。与图5(b)比较(二者的观测场景相同)，可见，相对飞机，同步轨道卫星作为发射端时杂波角度-多普勒曲线的距离依赖性很小。这验证了2.3节的结论。

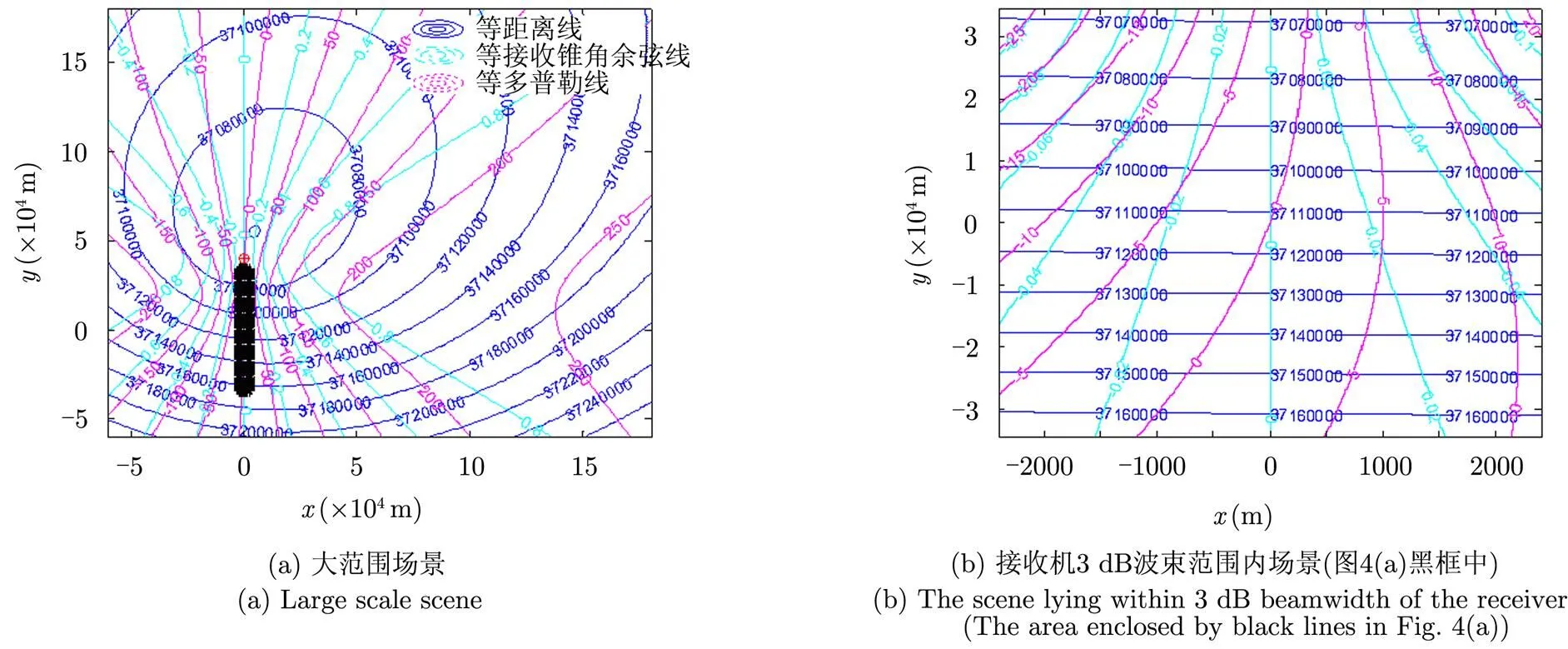
图4 等距离线、等多普勒线、等接收锥角线在场景中的分布

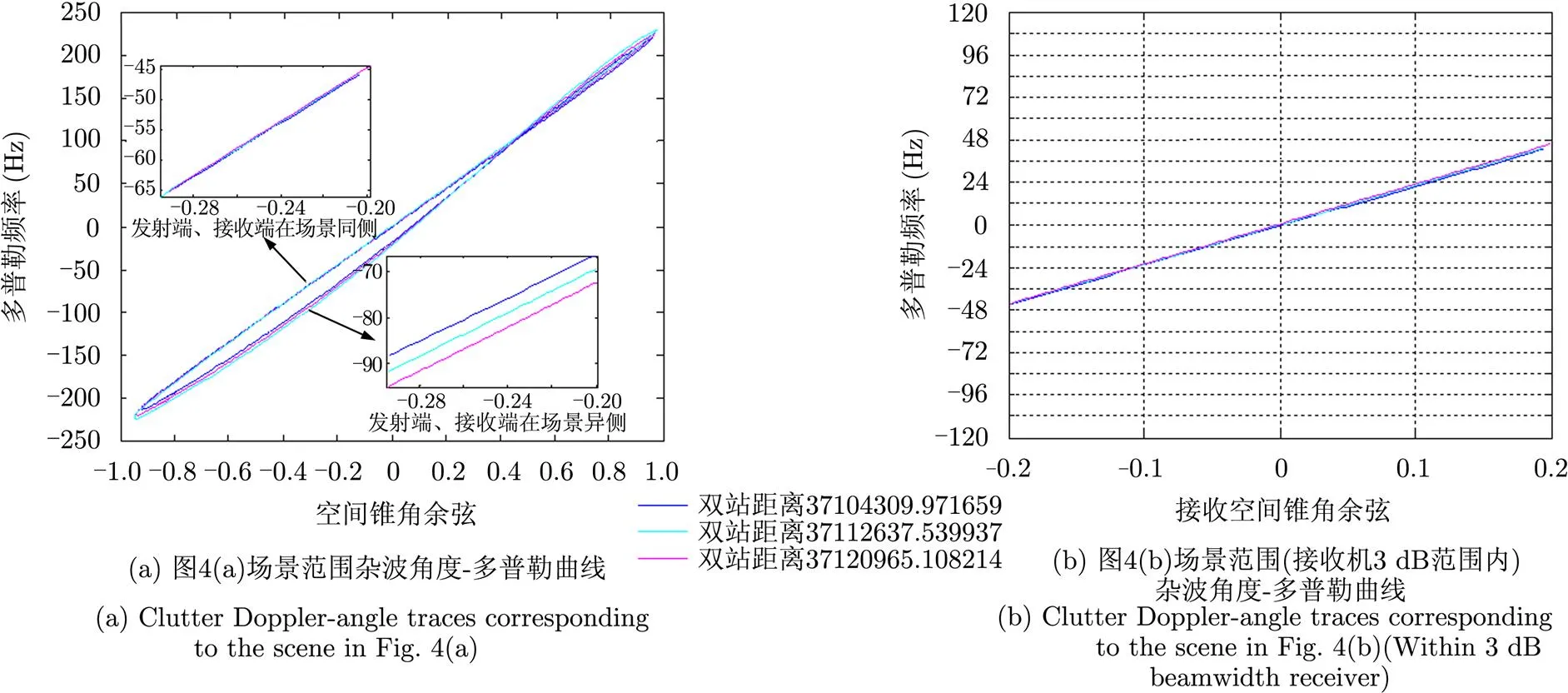
图5杂波角度-多普勒曲线

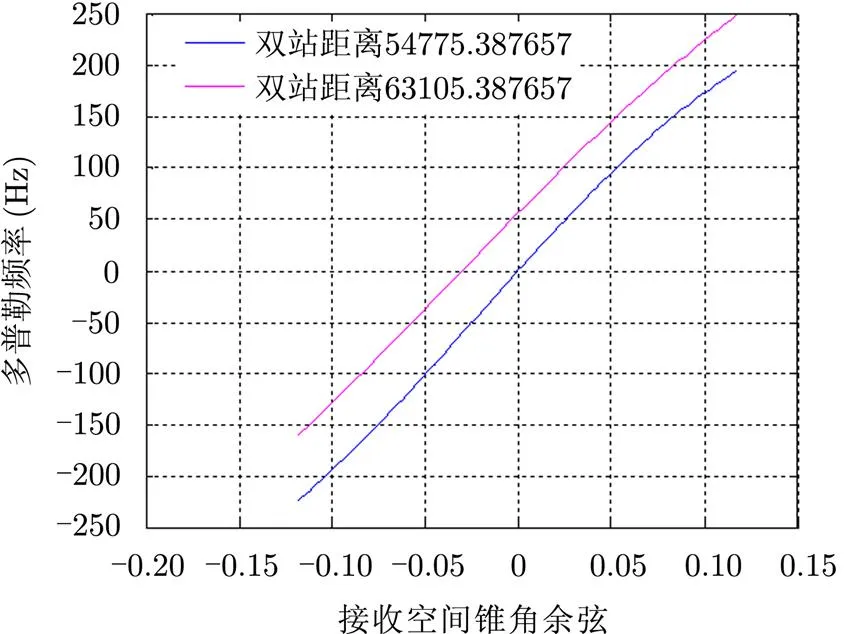
图6飞机作为发射端时接收机3 dB波束范围内的杂波角度-多普勒曲线

4 结束语

本文分析了同步轨道星-空双站SAR构型下杂波的特性，通过分析和仿真实验得出，相对于机载双站构型，同步轨道星-空双站构型下，杂波特性的距离依赖性较弱。本文为应用STAP方法抑制杂波提供了依据，为同步轨道星-空双站构型下进行动目标检测提供了参数设计依据。

附录A

由式(3)，同步轨道星-空双站构型下，接收信号的瞬时多普勒频率为

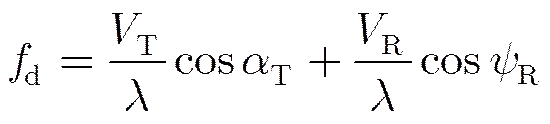
其中，

(A-2)

下面在接收空间锥角一定的条件下，通过中间变量求多普勒频率对双站距离偏导数。设基线在-平面的投影为，发射端至目标的距离，接收端至目标的距离在-平面的投影分别为,，接收端和发射端在场景坐标系下的高度分别为，则有

(A-4)

(A-6)

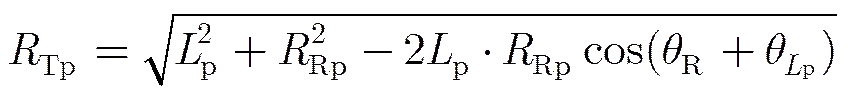
(A-8)

由式(A-8)，双站距离可写为

(A-10)

发射端俯仰角余弦为

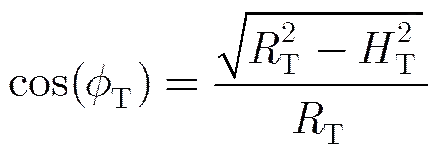
由式(A-9)及隐函数求导法则(见附录B)，可得

(A-12)

附录B

则有

(B-2)

又由式(A-8)得

(B-4)

由隐函数求导法则，可得

由式(B-2)-式(B-5)可求得式(A-12)。

[1] Guttrich G L and Sievers W E. Wide area surveillance concepts based on geosynchronous illumination and bistatic unmanned airborne vehicles or satellite reception[C]. Proceedings of the IEEE national Radar Conference, Syracuse, NY, USA, 1997: 126-131.

[2] 仇晓兰, 丁赤飚, 胡东辉. 双站SAR成像处理技术[M]. 北京: 科学出版社, 2010: 8-11.

Qiu Xiao-lan, Ding Chi-biao, and Hu Dong-hui. Bistatic SAR Imaging Algorithms[M]. Beijing: Science Press, 2010: 8-11.

[3] Raney R K. Synthetic aperture imaging radar and moving targets[J]., 1971, 7(3): 499-505.

[4] Chiu S and Dragosevic M V. Moving target indication via RADARSAT-2 multichannel synthetic aperture radar processing[J]., 2010, 2010: 1-12.

[5] Dragosevic M V and Chiu S. Extending airborne SAR-ATI algorithms to the RADARSAT-2 Moving Object Detection Experiment(MODEX)[C]. International Geoscience and Remote Sensing Symposium(IGARSS), Boston, USA, 2008: I-165-I-168.

[6] Chiu S. Performance analysis of RADARSAT-2 multi- channel MODEX modes[C]. Proceedings of 4th European Radar Conference, Munich, Germany, 2007: 170-173.

[7] Ender J H G, Berens P, Brenner A R,.. Multi-channel SAR/MTI system development at FGAN: from AER to PAMIR[C]. Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Toronto, Canada, 2002: 1697-1701.

[8] Nohara T J, Weber P, Premji A,.. SAR-GMTI processing with Canada's Radarsat-2 satellite[C]. IEEE 2000 Adaptive Systems for Signal Processing, Communications, and Control Symposium, AS-SPCC, Lake Louise, Canada, 2000: 379-384.

[9] Klemm R. Comparison between monostatic and bistatic antenna configurations for STAP[J]., 2000, 36(2): 596-608.

[10] Xu Jia, Liu Run-hua, Yeh Chun-mao,.. Clutter modeling for bistatic SAR with phased array antenna and arbitrary geometry configuration[C]. Proceedings of IEEE Radar Conference, Pasadena, CA, USA, 2009: 1-5.

[11] Zhang Y and Himed B. Effects of geometry on clutter characteristics of bistatic radars[C]. Proceedings of IEEE Radar Conference, Huntsville, AL, USA, 2003: 417-424.

[12] Liu Jin-hui and Liao Gui-sheng. Spaceborne-airborne bistatic radar clutter modeling and analysis[C]. IEEE CIE International Conference on Radar, Beijing, China, 2011: 915-918.

[13] 史洪印, 周荫清, 陈杰. 同步轨道星机双基地三通道SAR 地面运动目标指示算法[J]. 电子与信息学报, 2009, 31(8): 1881-1885.

Shi Hong-yin, Zhou Yin-qing, and Chen Jie. An algorithm of GEO spaceborne-airborne bistatic three-channel SAR ground moving target indication[J].&, 2009, 31(8): 1881-1885.

[14] Li Gang, Xu Jia, Peng Ying-ning,.. Bistatic linear antenna array SAR for moving target detection, location, and imaging with two passive airborne radars[J]., 2007, 45(3): 554-565.

[15] 包敏, 周鹏, 保铮, 等. 地球同步轨道SAR曲线轨迹模型下的改进CS成像算法[J]. 电子与信息学报, 2011, 33(11): 2686-2693.

Bao Min, Zhou Peng, Bao Zheng,.. An improved CS imaging algorithm for GEO SAR based on curve trajectory model[J].&, 2011, 33(11): 2686-2693.

[16] 魏钟铨. 合成孔径雷达卫星[M]. 北京: 科学出版社, 2001: 139-140.

Wei Zhong-quan. Synthetic Aperture Radar Satellite[M]. Beijing: Science Press, 2001: 139-140.

Analysis of Geosynchronous Satellite-Air Bistatic SAR Clutter Characteristics from the Viewpoint of Ground Moving Target Indication

Zhang Dan-danQiu Xiao-lanHu Dong-huiDing Chi-biao

(Institute of Electronics, Chinese Academy of Sciences, Beijing 100190, China)(Key Laboratory of Spatial Information Processing and Application System Technology,Chinese Academy of Sciences, Beijing100190, China)(University of Chinese Academy of Sciences, Beijing 100190, China)

Considering the geometry of geosynchronous satellite-air bistatic Synthetic Aperture Radar (SAR) where the geosynchronous satellite is the transmitter and the aerostat is the receiver, to suppress clutter and detect a slow-moving target using Space-Time Adaptive Processing (STAP), it is necessary to analyze the clutter characteristics. From the viewpoint of a ground moving target indication, a theoretical model of the clutter characteristics considering the geometry of geosynchronous satellite-space bistatic SAR is analyzed and established in this study; in particular, the range-dependence characteristics of the angle-Doppler curve of the clutter is analyzed. Finally, the simulation verifies the correctness of the analysis. The theoretical model described and the conclusion presented in this paper indicate the clutter characteristics of the new geosynchronous satellite-air bistatic SAR mode and provide a theoretical basis for the selection and research of a ground moving target indication method for use in this mode.

Geosynchronous; Bistatic; Ground Moving Target Indication (GMTI); Clutter characteristics; Range dependence

TN953

A

2095-283X(2013)03-0348-09

10.3724/SP.J.1300.2013.13006

2013-01-11收到，2013-04-22改回；2013-04-28网络优先出版

国家自然科学基金(61101200)资助课题

张丹丹 zhangddbb@yeah.net

张丹丹(1986-)，女，博士生，主要研究方向为合成孔径雷达-地面运动目标检测(SAR-GMTI)。

E-mail: zhangddbb@yeah.net

仇晓兰(1982-)，女，副研究员，主要研究方向为双站SAR成像、干涉SAR、SAR-GMTI等。

胡东辉(1970-)，男，副研究员，主要研究方向为SAR数据处理、干涉SAR、SAR-GMTI、ISAR成像等。

丁赤飚(1969-)，男，研究员，博士生导师，主要从事SAR、遥感信息处理和应用系统等领域的研究工作。