基于贝叶斯框架的空间群目标跟踪技术

黄 剑* 胡卫东



基于贝叶斯框架的空间群目标跟踪技术

黄 剑胡卫东

(国防科技大学电子科学与工程学院ATR重点实验室 长沙 410073)

对大量密集的空间群目标进行有效跟踪、编目已成为空间监测的迫切需求。地基雷达作为近地轨道空间监测的主要手段，在对高密度的空间小碎片云进行跟踪时，通常会由于分辨能力有限，造成对个体目标检测、观测信息严重缺失，使得传统的多目标跟踪技术难以奏效。为此，该文基于“群”跟踪的概念，在贝叶斯框架下以群目标的整体运动趋势为跟踪对象，同时兼顾个体的运动目标轨迹跟踪，通过建立群目标的中心和观测量之间的相互作用约束模型，可以提升在漏警概率较高情况下的目标数目估计的稳健性以及单个目标的跟踪精度。贝叶斯积分的求解过程通过MCMC-Particle算法具体实现。通过对空间群目标跟踪的仿真实验验证了群跟踪技术的有效性。

空间监测；群目标；空间目标；轨道跟踪；贝叶斯框架

1 引言

随着近地轨道空间目标数目，特别是空间碎片的日益增多，空间监测已成为有效利用空间资源预防空间碎片威胁的重要基础。现有的空间监测网大多只能够对10 cm以上的空间碎片进行个体编目跟踪，然而，更多的1 cm以上的小碎片对航天器都会产生致命的威胁，这类空间碎片大多会以高密度的碎片云形式成“群”出现。雷达是近地轨道空间监测的主要手段，在雷达分辨能力不足的情况下，独立的对其进行个体的跟踪和编目，其难度很大。对多个空间目标以“群”的方式进行跟踪和编目已成为继传统的个体空间目标编目以来的迫切需求和发展趋势。同时，碰撞预警作为空间监测的一个重要应用，它通常采用预测的协方差“管道”进行碰撞概率的估算，而“群”也是一个描述多个相近目标的整体运动轨迹的“管道”，可以很好地适应于应用需求。空间目标群可以定义为在跟踪时段内轨道根数相接近，不易于区分的目标群体。无论是轨道根数尚未散开的碰撞产生的碎片云，还是伴随飞行的编队卫星，它们都具备典型的群组特征。对群目标整体进行跟踪和编目，既能够利用“群”的动态模型描述多目标运动的整体趋势，同时也可以提升对个体跟踪的精确性，对于空间态势感知、碰撞预警具有重要意义。

群目标跟踪问题有别于传统的多目标跟踪问题。多目标跟踪问题中对目标个体的观测量与实际状态量较为吻合，个体运动特征明显。而群目标的跟踪问题则由于目标的密集程度超过了传感器分辨能力等因素导致个体信息缺失严重，漏警概率更高，其观测结果中，宏观的整体运行规律相对于个体运动轨迹同样重要。跟踪问题的差异将会导致关注对象、先验信息的利用以及技术途径的不同。在传统的多目标跟踪方法中，多目标假设(Multiple Hypothesis Tracking, MHT)跟踪算法和JPDA (Joint Probabilistic Data Association)算法是跟踪性能很好的两类经典算法，它们在解决多目标关联问题的基础上实现对多个个体目标的跟踪。为了减小运算的复杂度和实现未知数目的多目标跟踪，Mahler提出了利用随机集跟踪扩展目标的方法，基于一阶贝叶斯滤波器，将概率密度假设(Probability Hypothesis Density, PHD)算法扩展应用于含有群的运动和信息的情况。在此基础上，Vo等人针对高斯噪声情况下，得到高斯混合PHD算法的解析式，同时为了获得更加稳定的目标数目估计，更高阶的CPHD (Cardinalized PHD)、GMCPHD (Gaussian Mixture CPHD)算法相继被提出并得到广泛应用，但是这些算法不能清晰地对个体目标轨迹进行确认，而且在高杂波和低检测概率的情况下跟踪性能并不理想。为了提升多目标的跟踪性能，仅进行多个独立的个体跟踪的方法具有一定的局限性。于是，Khan等人利用MCMC (Markov Chain Monte Carlo)算法，充分考虑蚂蚁群体目标间的相互作用的关系，建立了描述蚁群运动的相互保持一定距离的隐马尔科夫模型，成功地对实际拍摄的蚁群进行了跟踪试验，促进了含相互作用关系的多目标跟踪技术的发展。然而，阻碍群目标跟踪发展最大的问题之一就是对“群”的分裂与合并的描述，Pang等人充分考虑群内目标的中心趋向运动和目标间的相互作用，对多目标的分组运动模型以及群的合并和分离问题建立了一套相对完整的机制，利用目标群的先验信息大大提升了多目标在密集杂波、低检测概率环境下的跟踪精度和目标数目估计的正确性。在图像视频跟踪领域，像Mean-Shift这类算法则直接忽略个体的运动趋势，以区域像素点的概率分布作为跟踪的对象，实现对关注对象的整体跟踪。

针对空间群目标的跟踪问题，空间目标密度尚未达到图像跟踪中的像素密度，但同时受限于雷达分辨力，已经超出了多目标个体跟踪的密度。因此，我们以群目标的整体运动趋势为跟踪对象，同时兼顾个体的运动目标轨迹跟踪。首先，在分析空间目标运动特征的基础上构造能够描述“群”的运动特征参数和结构变量，在贝叶斯框架下对群目标进行跟踪。通过建立群目标的中心和观测量之间的相互作用约束模型，不仅可以得到“群”的特征描述，同时可以大大提升在漏警概率较高情况下的目标数目估计的稳健性以及单个目标的跟踪精度。贝叶斯的求解过程通过MCMC-Particle算法具体实现。

本文结构如下：第2节介绍了空间目标的运动模型、“群”的特征参量和结构模型，以及“群”的贝叶斯跟踪模型；第3节对贝叶斯跟踪过程进行了求解，分模块具体描述了空间目标的状态转移模型、群中心的状态转移模型、群中心与个体目标相互约束的模型以及观测模型；第4节采用MCMC- Particle算法实现以上贝叶斯估计的跟踪过程；第5节为对空间群目标进行跟踪的仿真实验及性能分析；第6节为结论。

2 空间群目标跟踪的贝叶斯模型

2.1空间群目标的运动和观测模型

空间目标在特定时刻的3维空间中的位置矢量和速度矢量可以确定目标的运动状态。首先定义参数如下：第个目标，在时刻的状态为,其中表示位置矢量，表示速度矢量。表示时刻的个目标的状态。在较短时间内，单个空间目标的轨道预测及预测误差可以采用简化的转移矩阵式(1)进行表示，但是其状态转移过程是高度非线性的，状态转移矩阵没有解析解，都需要对开普勒方程进行迭代求解：

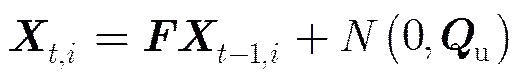
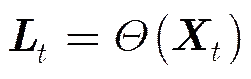
目标的观测模型如式(3)所示：

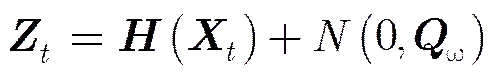
2.2目标群中心跟踪的贝叶斯模型

在本文中，选择多个目标运动状态的均值中心描述群运动的特征参数：

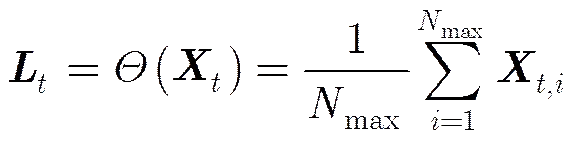
群中心的运动方程表示如式(5)：

(5)

这样，就可以利用一个群中心对多个目标个体进行约束，使得在低检测概率的跟踪过程中的目标数目不至于剧烈跳变、目标的运动轨迹保持连续性和稳定性，同时也可以对群目标的整体轨迹进行跟踪和预测，对于提升个体目标跟踪性能具有重要意义。

同时，为了描述群内多个目标运动过程中整体结构的变化情况，我们定义时刻多个目标的存在状态，其中。当对应于中第个目标的存在，则表示目标的消失。如图1所示为群目标跟踪状态转移示意图。

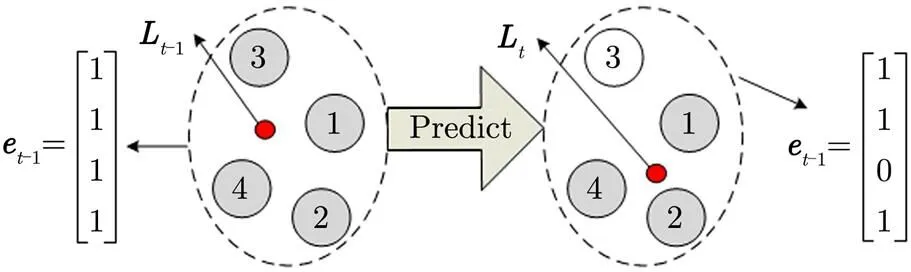
图1 群目标跟踪状态转移示意图

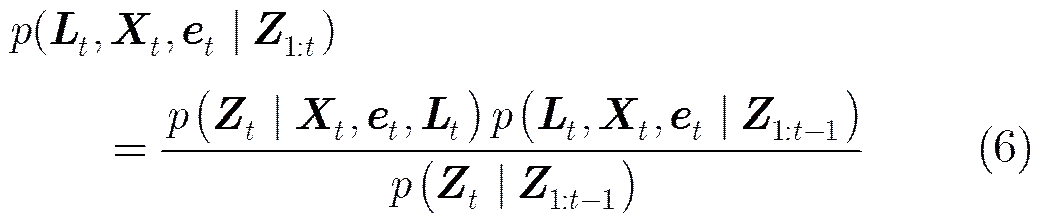
从式(6)和式(7)可以看到，在后验概率的计算中，核心问题是状态转移概率的计算。

3 贝叶斯模型的求解

对空间目标群的贝叶斯跟踪模型进行求解，首先将式(7)中的转移概率模型扩展为

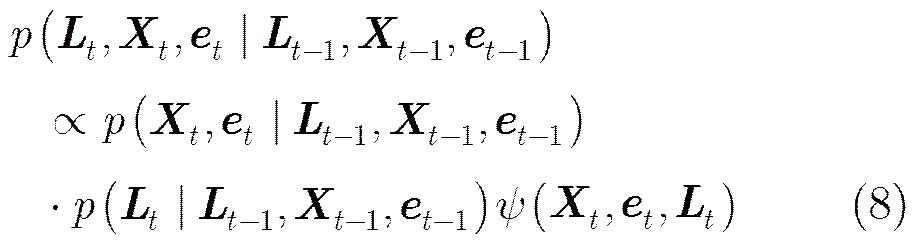
3.1目标状态预测的动态模型

通过对上一时刻各个目标运动状态进行预测可以得到多个目标当前状态，本文忽略上一时刻群中心的状态对各个目标状态预测的情况，则目标状态的预测模型可以展开为式(9)：

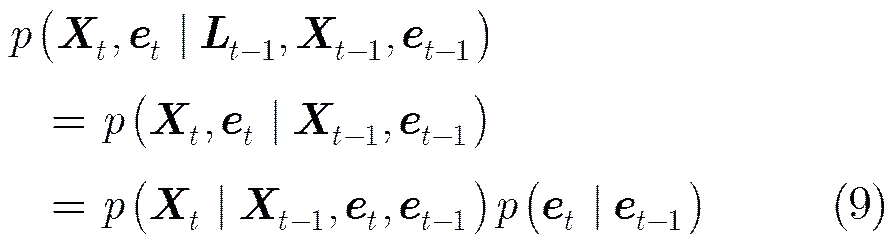
其中，表示目标存在状态的变化，也可以看作一个简单的群结构的转换，为基于存在状态的目标状态预测。

3.1.1目标群的存在状态结构的转换模型 在本文跟踪过程中，为了节约计算和存储资源，对目标数目设定最大存在的目标的个数为，这也是符合实际情况的，则

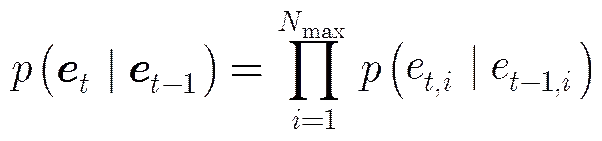
其中每个目标的存在和消失的状态转移概率都预先设定合理的参数，通常情况下，为了能够快速跟踪到新目标和保证目标的连续性，因此对新目标产生的概率和已有目标的保持概率的取值会大于目标消失的概率。具体参数选择跟实际情况相关，而且跟踪结果好坏对参数大小并不敏感。当每个目标的存在状态以一定概率变化，则群目标的整体的存在状态变化就会体现出一定的群结构变换趋势。

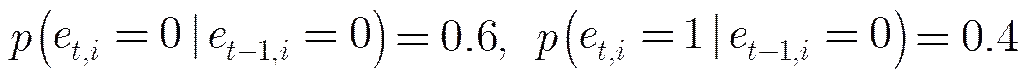
从图3可以看出群目标存在状态转移的概率分布情况，它表明群目标从状态转移到状态的概率只有0.0032，而保持状态不变的概率有0.3072。这也是一种维持目标群整体结构稳定的一种方式。在已知存在状态转移的概率后，就可以对目标运动状态进行预测。

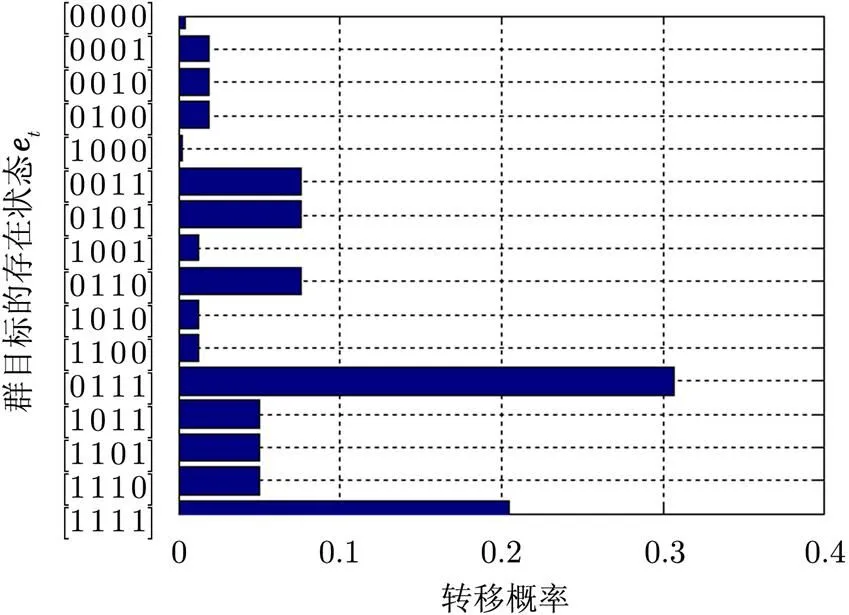
图3 群目标存在状态转移的概率分布

3.1.2目标的运动状态转移模型 目标的状态转移模型根据和的不同分别采用不同模型进行刻画。设代表和的目标集合，即代表新目标产生。为的目标集合，表示目标的消失和不存在。代表和的目标集合，即需要进行预测更新的目标。,和分别为不同集合对应的目标个数。

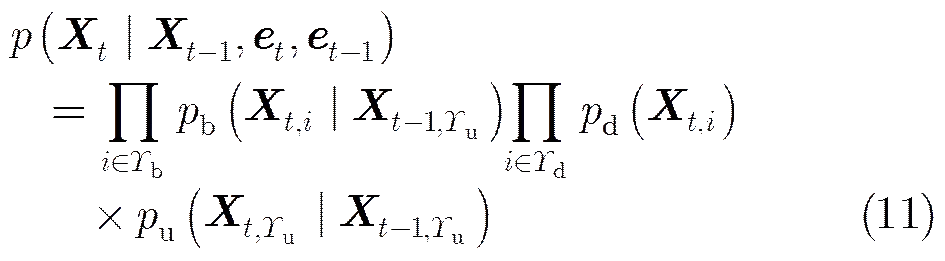
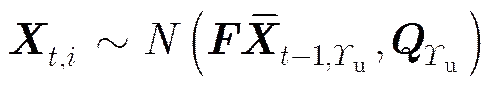
因此

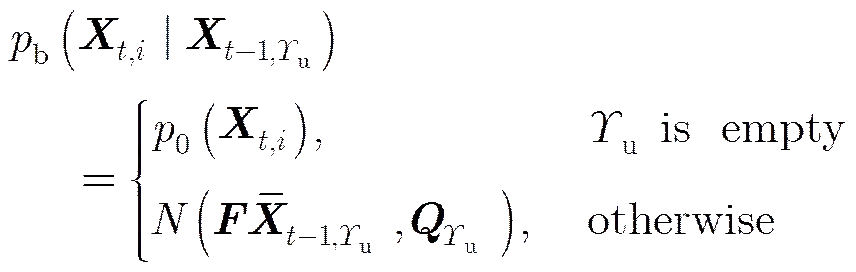
(15)

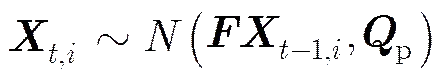
3.2群中心的预测模型

目标群的中心拥有比单个目标更加稳定的运动趋势和更高的检测概率，群中心的预测需要保证中心运动方向的延续性。假设时刻，多个目标的存在状态的概率为，而不同的目标存在状态就会形成不同的群结构，从而群中心也会不同。为了防止因为预测的群中心种类过多导致分组状态的发散即群中心的漂移，对小于一定概率的分组模式置零，可取0到0.5之间的小数字(如0.3)：

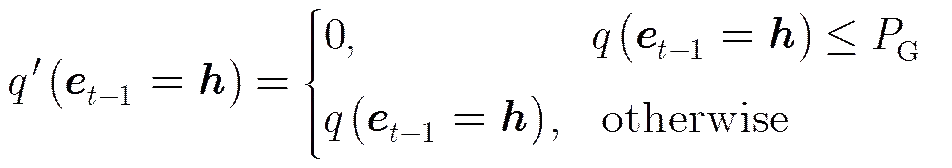
归一化分组模式概率

(18)

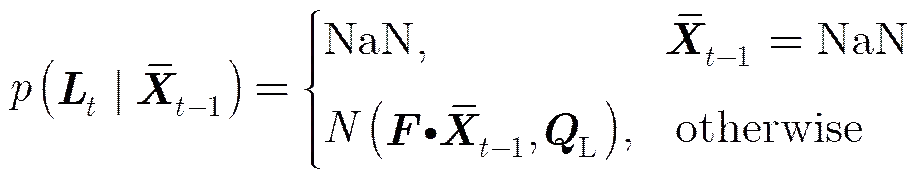
(20)

3.3群中心与个体目标之间的关联概率

群中心与预测的多目标的运动状态都是目标群运动规律的体现，二者是同源的，因此它们之间存在一定的相互作用关系。本文采用关联概率来描述其特性。在预测得到时刻的目标运动状态，目标存在状态和群中心后，可以利用预测的群中心和预测的多个目标的均值中心的匹配程度来衡量其关联概率。

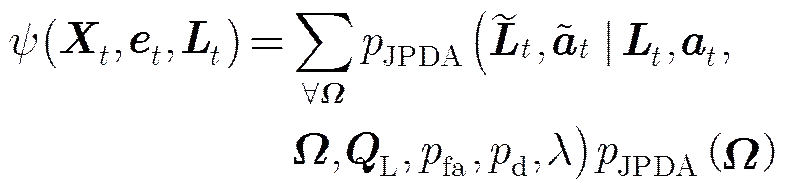
式(21)的计算过程见附录Ｂ。这样就能得到预测的群中心和多个目标运动状态相互作用的隐马尔科夫模型的贝叶斯概率。通过这层约束关系，可以使得目标群的整体运动趋势保持延续性，能够在低检测概率、高密度杂波环境的情况下保证跟踪的稳健性。

3.4观测模型

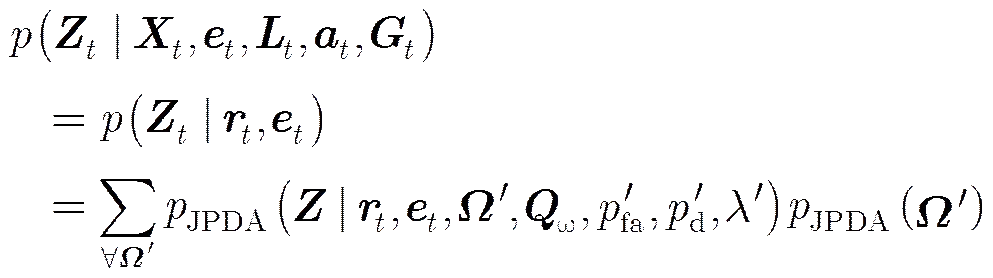
4 基于MCMC-Particle算法求解贝叶斯过程

以上贝叶斯的跟踪过程的概率计算是高度非线性，极为复杂，不容易得到解析解。MCMC算法是解决非线性概率分布递推、积分的有效工具，但通常运算量较大。本文采用参考文献中提出的改进MCMC-Particle算法进行贝叶斯概率分布的计算对第3节的贝叶斯过程进行求解。

MCMC算法主要通过计算接受概率

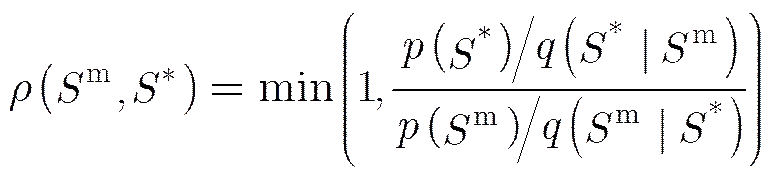
采用均匀分布产生随机的接受概率门限，二者比对决定粒子是否更新。其中表示当前的马尔科夫链的状态；表示马尔科夫链中目标状态的分布概率；表示根据当前状态以一定的概率分布采样一个候选样本。具体过程如下。

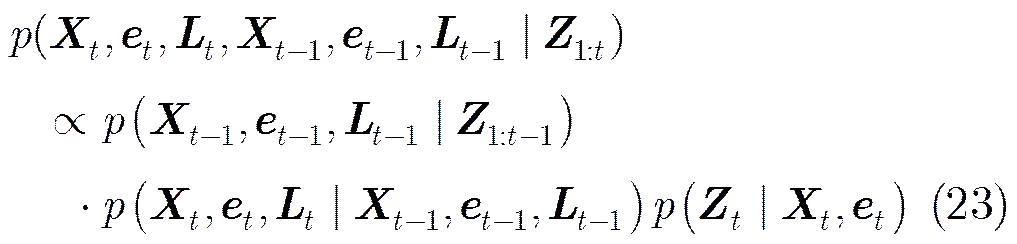
通过两步马尔科夫模型，可以更进一步的去除野值粒子，防止跟踪结果发散。对于时刻的后验概率分布，由于不能得到具体的分布形式，根据经验分布用个离子近似，即

整个MCMC-Particle算法过程的实现包括以下3个部分：

(1) 群中心采样

(2) 联合采样

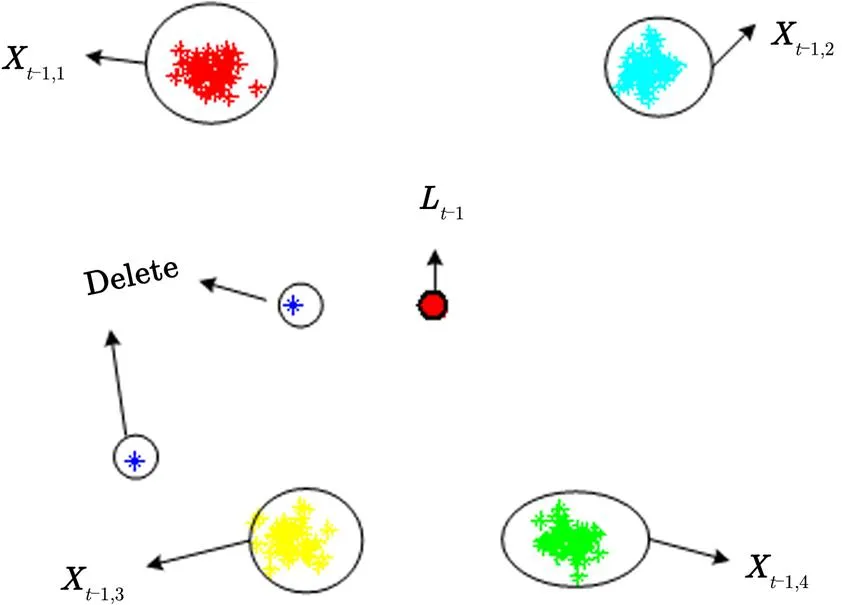
图4 跟踪粒子的聚类

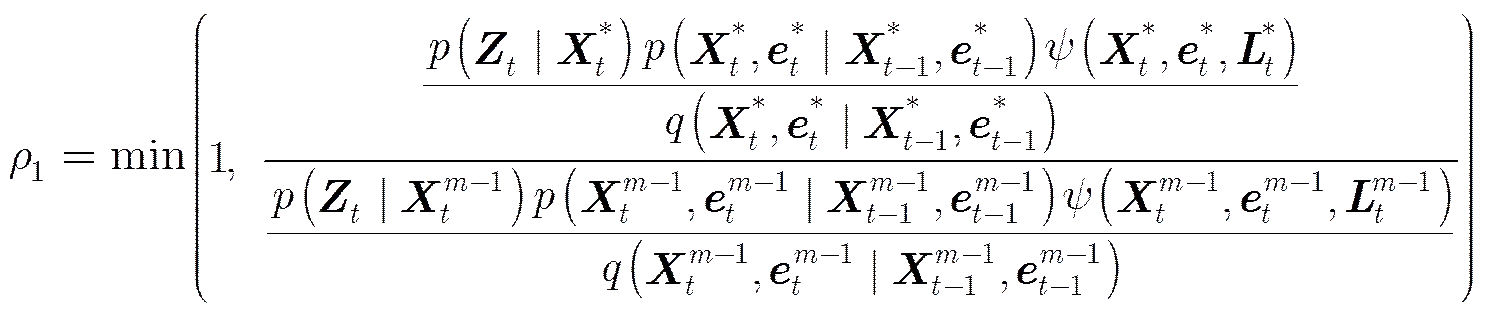
(3) 更新个体目标

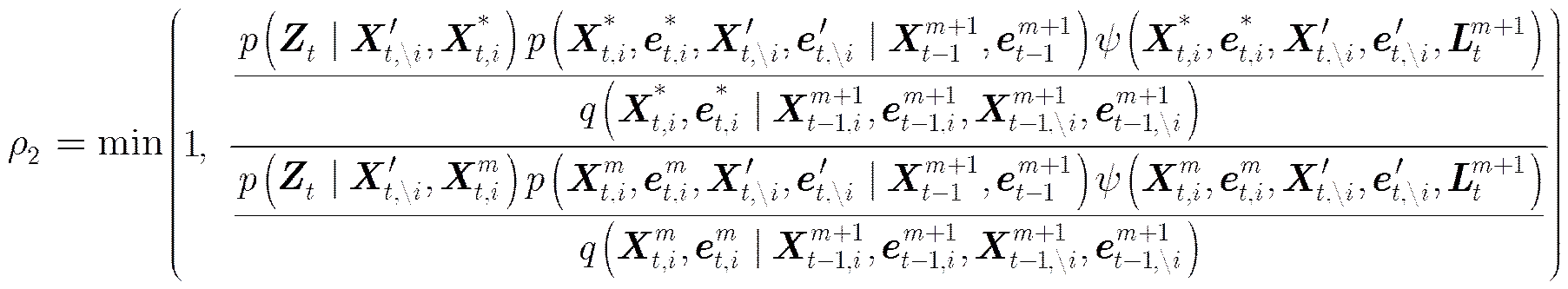
通过一定次数的MCMC-Particle的迭代计算不断更新粒子，去除部分老化粒子，则最终收敛后的粒子能够近似表示跟踪目标状态的后验概率估计。

5 仿真实验分析

基于MCMC-Particle算法的跟踪过程参数设置如表2。

观测轨道为零时刻轨道各自向前和向后延伸15 s，共30个观测点。4个空间目标组成一个目标群，仿真场景中真实目标运行轨迹和观测的目标位置轨迹如图5所示。

表1 仿真目标轨道根数情况

表2跟踪过程中参数设置情况

Tab. 2 The tracking parameters for the simulation results

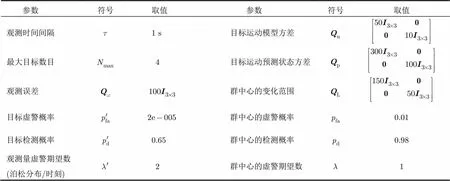
参数符号取值参数符号取值 观测时间间隔1 s目标运动模型方差 最大目标数目4目标运动预测状态方差 观测误差群中心的变化范围 目标虚警概率2e005群中心的虚警概率0.01 目标检测概率0.65群中心的检测概率0.98 观测量虚警期望数(泊松分布/时刻)2群中心的虚警期望数1

目标航迹的起始是假设真值以正态分布的形式存在于观测量附近，从而进行抽样取值。在每一个时刻，做5000次MCMC-Particle迭代算法，估计当前的目标状态，去除之前未收敛的2000个离子，在收敛后的粒子中抽样个粒子作为输出。

采用MCMC算法进行多目标的贝叶斯跟踪，其个体目标跟踪相对于其余跟踪的算法优越性已经在文献[11,12]中得以说明，本文主要对含群中心的群跟踪算法与文献[12]提出的不含群中心的跟踪算法的结果进行对比。

根据仿真场景的设置，得到原始的状态估计粒子分布情况如图6所示。

其中，图6(a)为含群中心的空间群目标的跟踪状态，图6(b)表示不含群中心的多个目标跟踪状态。可以看出群中心的跟踪不仅能够获得多个目标整体的运动趋势，同时对目标数目和个体运动状态的估计也更为准确，可以更加精确地重构真实轨迹。对每个时刻目标跟踪的状态粒子进行K-Means聚类，去除粒子中的野值点，根据这些粒子所带目标的标记，取均值作为对应目标的状态估计，估计结果如图7所示。

群目标的存在状态分布如图8所示。

通过仿真可以看出，群目标的跟踪相对于多目标个体进行跟踪，不仅能够获得重要的“群”的运动特征，在对多个目标存在状态结构的估计上也有很大改善。本文通过对场景进行30次独立的蒙特卡洛仿真对算法的跟踪性能进行对比。统计每个时刻所跟踪到的目标个数的均值和目标的状态估计的均方根误差(RMSE)如图9所示。

经过多次蒙特卡洛仿真，可以看出，空间群目标的跟踪相对于原有的多目标跟踪可以更加准确地估计群目标中含有的真实目标数目，大大降低了漏警概率，同时对于位置和速度的估计误差也相对更低。而且，群中心的跟踪状态也可以为跟踪结果提供较为稳定的宏观信息。实际上群目标跟踪之所以能够提升低检测概率情况下的目标数目估计的正确性，是因为在跟踪中，群中心的状态更加稳定、不易改变，而目标个体检测概率很低，起伏很大。本文设群中心的检测概率为0.98，而目标个体的检测概率只有0.65。在跟踪过程中加入群中心的约束必然会大幅提升跟踪性能，这也是“群”的先验信息的应用带来的优势。

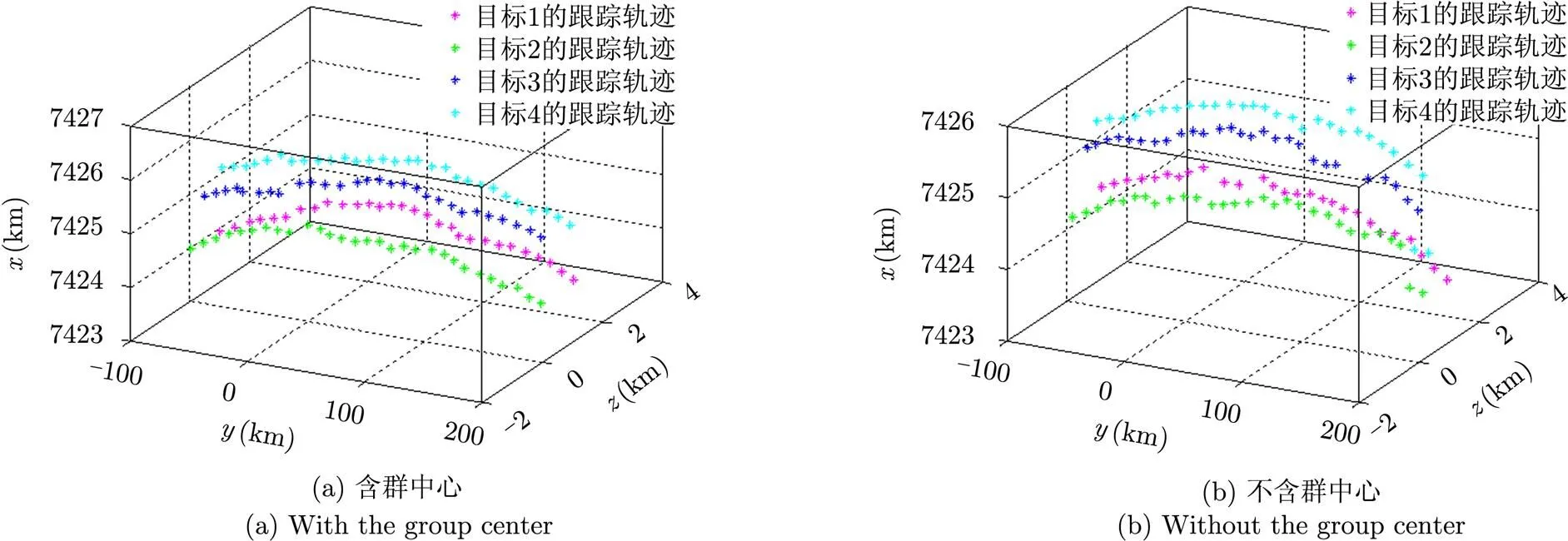
图7 群目标跟踪状态估计结果

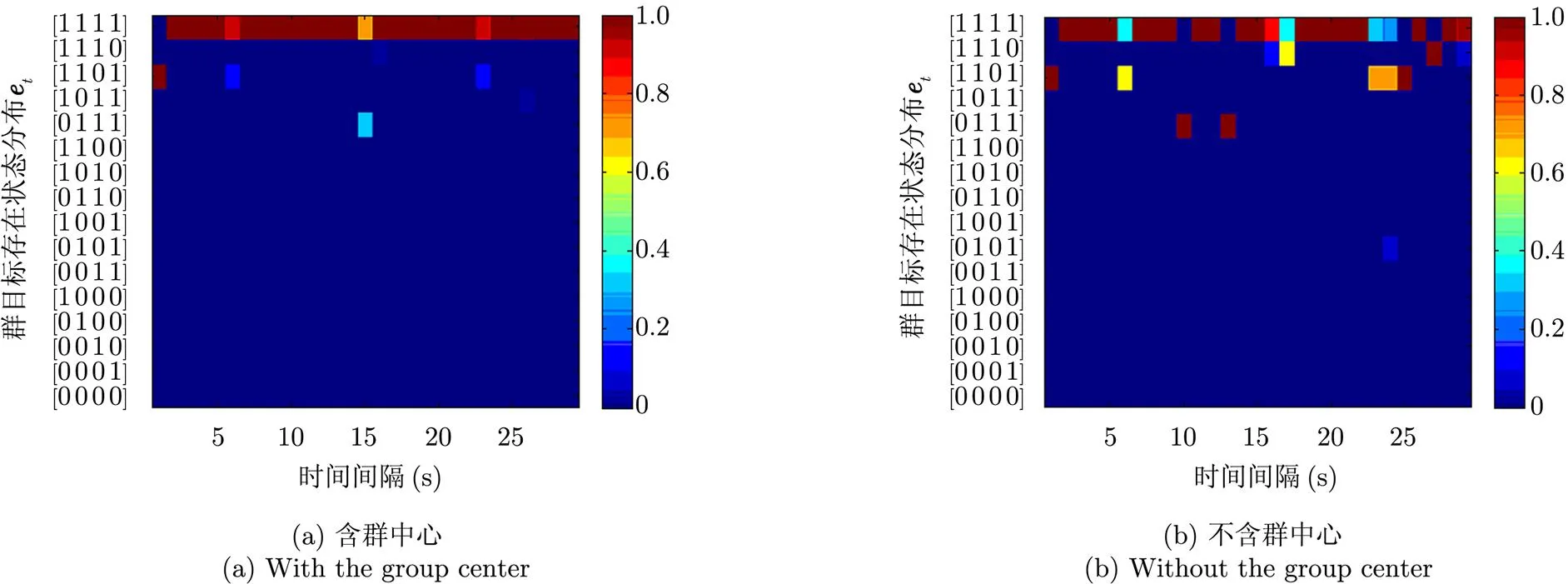
图8 群目标存在状态分布情况

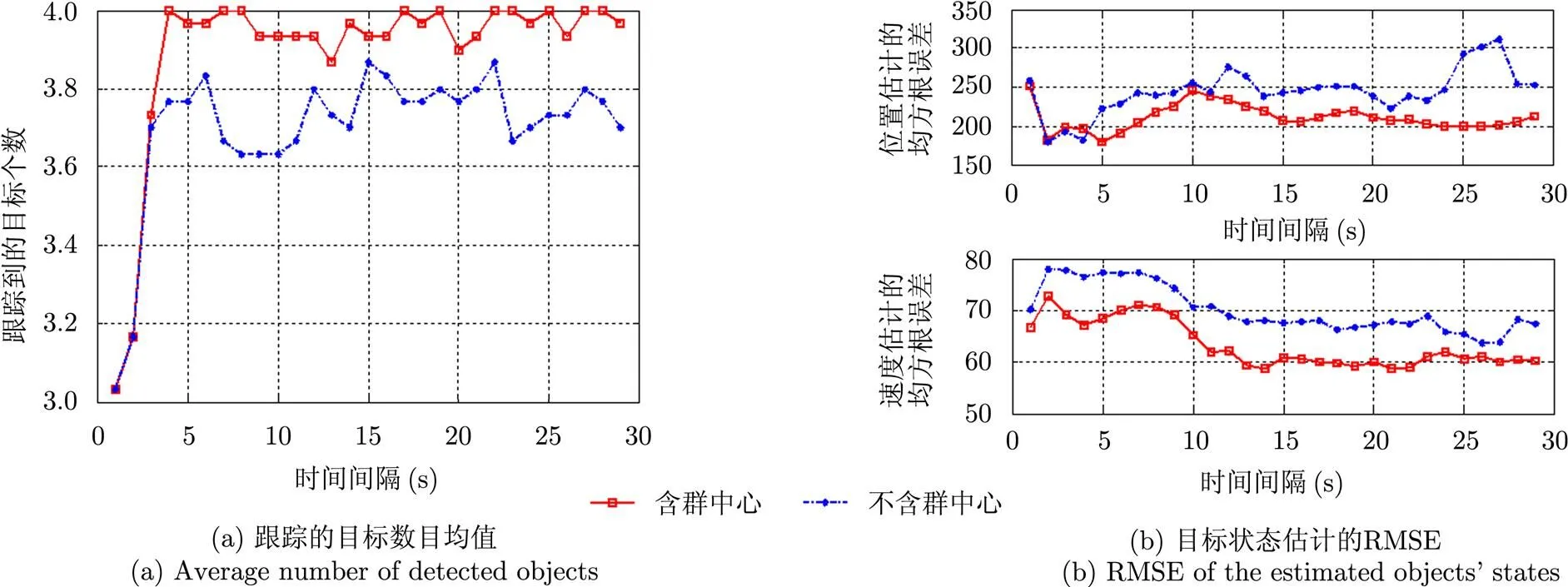
图9 基于30次蒙特卡洛仿真群目标跟踪性能分析

6 结论

空间群目标的跟踪是空间监测领域中的一个前沿方向和潜在需求，无论对于真假弹头、诱饵群的预警跟踪，还是空间碎片群以及编队卫星的编目问题都具有重要意义。

本文首先提出了群跟踪这样一个概念，描述了空间群目标的运动模型，根据空间目标的运动特性构造了群中心跟踪的贝叶斯过程，并利用MCMC-Particle算法进行求解，并通过对空间目标的模拟轨道进行跟踪试验，验证了在高杂波、低检测概率环境下算法对于群跟踪的有效性，相对无群中心时提升了目标数目估计的稳健性、估计精度。本文提出的“群”中心跟踪的概念只是众多“群”特征中的一个，根据应用背景的不同具有不同的存在形式，同时也可以充分利用群组的隐含先验信息构造各种有效的MRF模型提升跟踪性能，但是“群”跟踪的概念本身具有更为重要的意义。

附录A 轨道目标状态转移矩阵

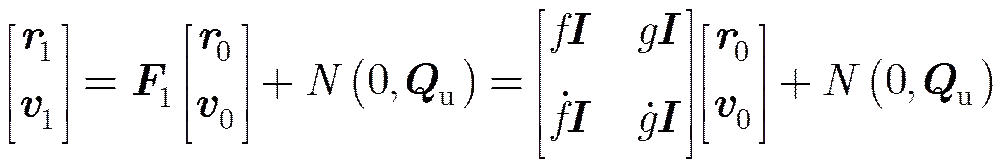
为了初始化轨道根数或者在原有跟踪过程中出现野值情况导致轨道为非椭圆轨道时。将轨道预测的状态转移方程近似为圆轨道进行处理，即偏心率(Eccentricity)的情况，在此基础上适当调整速度矢量，可以实现对小偏心率轨道的预测和跟踪。圆轨道空间目标，当位置矢量已知时，若轨道倾角(Inclination)已知，则轨道就完全确定下来。其位置矢量和速度矢量满足方程(A2)：

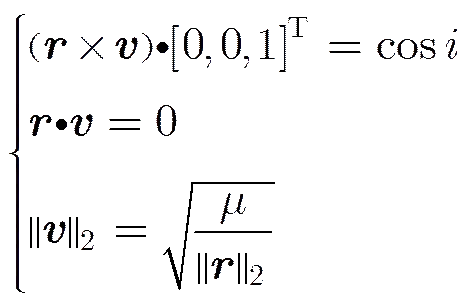
正负号的选择根据轨道倾角和位置矢量唯一确定。

这时可以得到转移矩阵式(A4)：

因此，空间目标的运动状态转移方程可以记为式(A5)：

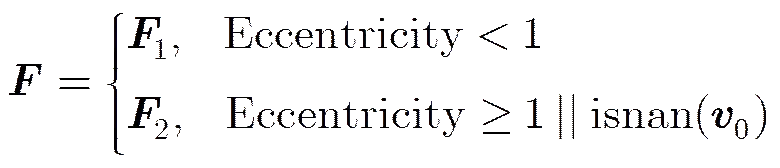
附录B JPDA关联概率计算

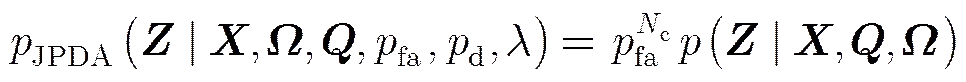
(A7)

因此可以得到JPDA关联概率如下式：

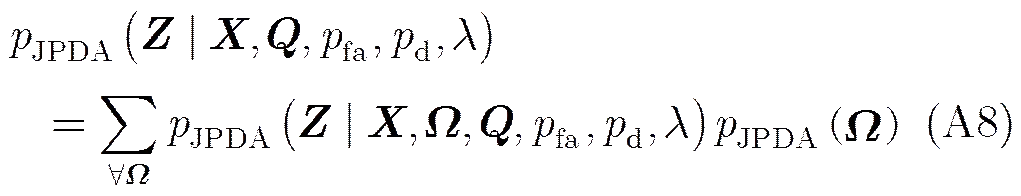
[1] Liou J C and Shoots Debi. Orbital debris quarterly news[R]. NASA, 2009, Report Number: JSC-CN-18100.

[2] Nicholas L Johnson. The world state of orbital debris measurements and modeling[J]., 2004, 54(4): 267-272.

[3] Matney M J, Anz-Meador P, and Foster J L. Covariance correlations in collision avoidance probability calculations[J]., 2004, 34(5): 1109-1114.

[4] Reid D B. An algorithm for tracking multiple targets[J]., 1979, 24(6): 84-90.

[5] Fortmann T E, Bar-Shalom Y, and Scheffe M. Sonar tracking of multiple targets using joint probabilistic data association[J]., 1983, 8(3): 173-184.

[6] Ronald P S Mahler. Multitarget bayes filtering via first-order multi-target moments[J]., 2003, 39(4): 1152-1178.

[7] Ba-Ngu Vo and Wing-Kin Ma. The Gaussian mixture probability hypothesis density filter[J]., 2006, 54(11): 4091-4104.

[8] Ronald P S Mahler. PHD filters of higher order in target number[J]., 2007, 43(4): 1523-1543.

[9] Ba-Tuong Vo, Ba-Ngu Vo, and Antonio Cantoni. Analytic implementations of the cardinalized probability hypothesis density filter[J]., 2007, 55(7): 3553-3567.

[10] Ng William, Li Jack, Godsill S J,.. Multitarget initiation, tracking and termination using Bayesian Monte Carlo methods[J]., 2007, 50(6): 674-693.

[11] Zia Khan, Tucker Balch, and Frank Dellaert. MCMC-Based Particle Filtering for tracking a variable number of interacting targets[J]., 2005, 27(11): 1805-1819.

[12] Pang Sze Kim, Li Jack, and Godsill S J. Detection and tracking of coordinated groups[J]., 2011, 47(1): 472-502.

[13] Dofin Comaniciu, Visvanathan Bamesh, and Peter Meer. Kernel-based object tracking[J]., 2003, 25(5): 564-577.

[14] Gim J Der. An elegant state transition matrix[J]., 1997, 45(4): 371-390.

[15] Howard D Curtis. Orbital Mechanics for Engineering Students[M]. Elsevier Butterworth Heinemann, 2005.

[16] Bar-Shalom Yaakov, Daum Fred, and Huang Jim. The probabilistic data association filter: estimation in the presence of measurement origin un-certainty[J]., 2009, 29(6): 82-100.

[17] Gilks W R, Richardson S, and Spiegelhalter D J. Markov Chain Monte Carlo in Practice[M]. Lynnfield, MA: Chapman and Hall/CRC, 1996.

[18] MacQueen J. Some methods for classification and analysis of multivariate observations[C]. Proceedings of the 5th Symposium on Mathematical Statistics and Probability, Berkeley, University of California Press, 1967: 281-297.

Tracking of Group Space Objects within Bayesian Framework

Huang Jian Hu Wei-dong

(ATR Key Lab, College of Electronic Science and Engineering, National University of Defense Technology, Changsha410073, China)

It is imperative to efficiently track and catalogue the extensive dense group of space objects for space surveillance. As the main instrument for Low Earth Orbit (LEO) space surveillance, ground-based radar systems are usually limited by their resolving power while tracking small, but very dense clusters of space debris. Thus, the information obtained regarding target detection and observation will be seriously compromised, making the traditional tracking method inefficient. Therefore, we conceived the concept of group tracking. The overall motional tendency of a group’s objects is particularly focused, while individual objects are in effect simultaneously tracked. The tracking procedure is based on the Bayesian framework. According to the restriction among the group center and observations of multi-targets, the reconstruction of the number of targets and estimation of individual trajectories can be greatly improved with respect to the accuracy and robustness in the case of high miss alarm. The Markov Chain Monte Carlo Particle (MCMC-Particle) algorithm is utilized to solve the Bayesian integral problem. Finally, the simulation of the tracking of group space objects is carried out to validate the efficiency of the proposed method.

Space surveillance; Group objects; Space object; Orbit tracking; Bayesian framework

TN971

A

2095-283X(2013)01-0086-11

10.3724/SP.J.1300.2013.20079

黄 剑(1986-)，男，湖北随州人，分别于2007年、2009年获国防科技大学学士学位、硕士学位，现为国防科学技术大学电子科学与工程学院博士研究生，研究方向为空间目标监测、雷达信息处理。E-mail: huangjian@nudt.edu.cn

胡卫东(1967-)，男，辽宁葫芦岛人，1997年获得国防科技大学通信与电子系统专业博士学位。现工作于国防科技大学ATR重点实验室，教授，中国航空学会信号与信息处理专业分会委员。目前研究方向为雷达信息处理、空间目标探测。E-mail: wdhu@nudt.edu.cn

2012-11-09收到，2013-01-05改回；2013-01-10网络优先出版

国家高技术研究发展计划项目(863计划)资助课题

黄剑 huangjian@nudt.edu.cn