机载干涉SAR区域网三维定位算法

毛永飞*① 汪小洁② 向茂生③



机载干涉SAR区域网三维定位算法

毛永飞汪小洁向茂生

(北京空间飞行器总体设计部 北京 100094)(北京系统工程研究所 北京 100101)(中国科学院电子学研究所微波成像技术国家重点实验室 北京 100190)

区域网3维定位是指同时获取多个干涉合成孔径雷达(InSAR)场景中各像素点的北向、东向和高程向的地理坐标。联合定标是区域网3维定位的关键环节，能够保证3维位置精度和相邻场景间的位置衔接性，并且能够在稀少控制点的条件下实现大区域多场景的3维定位。该文提出一种适用于机载InSAR系统的联合定标算法，该算法对多个场景的3维位置同时定标。该算法利用最优化模型实现联合定标，并且在最优化模型中引入了权值，从而顾及到了不同质量、不同分布的控制点、同名点在联合定标中的权重差异。机载InSAR实测数据的实验结果表明，该算法在3维定位精度和实现过程的简洁度方面均优于传统的联合定标算法。

合成孔径雷达；干涉；联合定标；3维定位；加权最优化

1 引言

干涉合成孔径雷达(Interferometric Synthetic Aperture Radar, InSAR)在地形测绘、灾害监测等领域有着广泛的应用，InSAR能够获得观测场景的图像信息和3维位置信息。机载InSAR数据处理流程主要包括：运动补偿、成像、复图像对配准、干涉条纹生成、相干系数计算、干涉条纹滤波、相位解缠、干涉定标、3维定位。精确的3维地理定位和几何校正是InSAR图像走向应用的前提和关键，系统参数误差、航迹参数误差以及系统非理想特性的存在，使得3维定位几何模型中的参数取值并不准确，需要通过干涉定标来校准各参数，以提高3维定位的精度。传统的干涉定标算法是利用3维位置信息已知的地面控制点(Ground Control Points, GCPs)，来闭环修正各干涉参数，其具体实现方法是基于线性化误差近似的敏感度方程迭代算法。

传统的InSAR定位算法通常分两步：首先进行高程定位，其次进行平面位置定位。其不足在于平面定位是建立在高程反演的基础之上，数字高程模型(Digital Elevation Model, DEM)的误差会在一定程度上影响平面定位精度。鉴于此，本文提出3维联合定位算法，即由干涉相位出发，同时获取目标的高程和平面位置(平面位置包括北向位置和东向位置，即纬度和经度)。

在机载InSAR系统测绘作业过程中，通常难以保证所有场景都布放有足够的控制点，因而必须采用联合定标算法来实现少量控制点条件下大区域多场景的干涉定标。传统的联合定标算法以单场景干涉定标为基础，利用同名点(Tie Points, TPs)进行3维位置信息的传递，进而实现所有场景的定标，但其不足在于：设计同名点位置信息的传递路径较为繁琐；难以顾及不同质量和分布的控制点和同名点在定标中的权重差异。鉴于此，本文提出了基于加权最优化模型的区域网3维联合定标算法，该算法能够同时对多个场景的高程和平面位置进行定标，并且能够方便地引入定标权值以顾及各控制点和同名点在定标中的权重差异，最后文中给出了定标权值的计算方法。

2 3维重建模型

在InSAR系统中，目标位于距离球、多普勒锥、干涉相位双曲面的交点处。距离球是以主天线相位中心为球心，以斜距为半径的球面；多普勒锥是以航迹方向为轴的圆锥，圆锥顶角的大小取决多普勒频率的大小；干涉相位双曲面是以两天线相位中心为焦点的双曲面。对目标进行3维定位即是对其距离方程、多普勒方程、干涉相位方程进行联立求解。但是，为了分析处理的方便，通常需要获得目标3维位置的闭式表达形式。

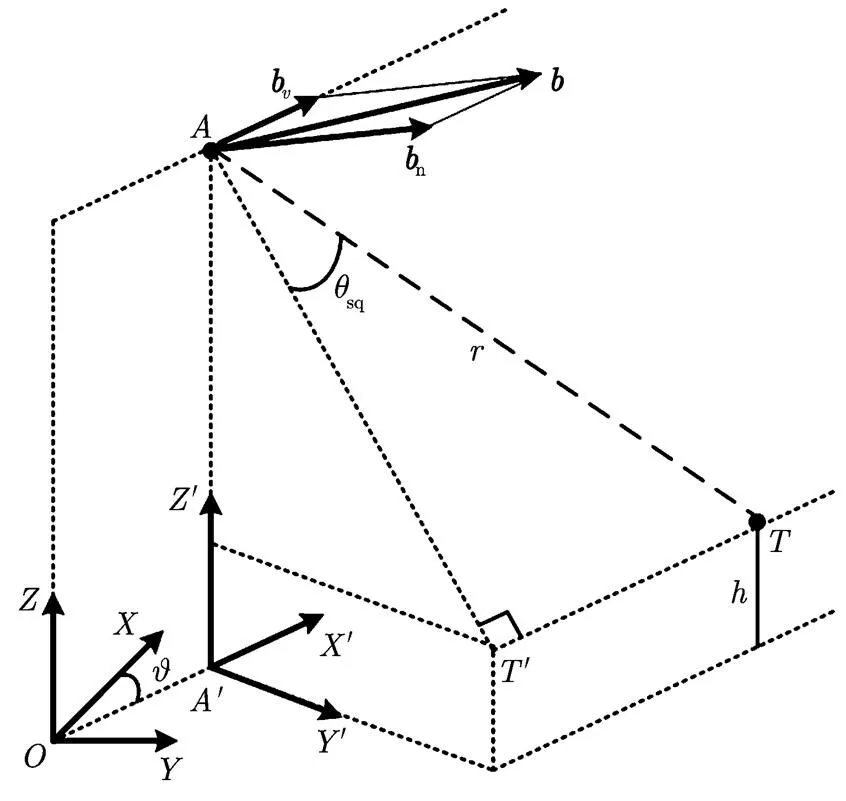
图1 机载InSAR 3维定位几何关系

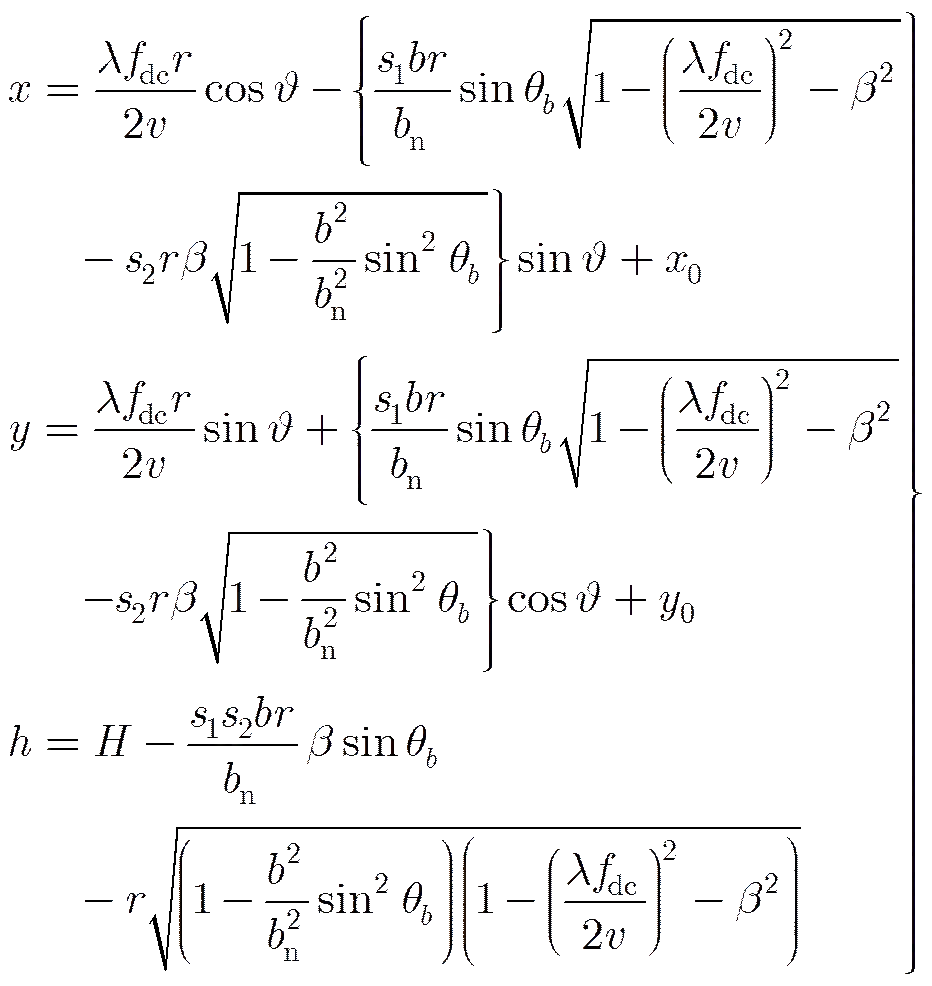
3 区域网3维定标算法

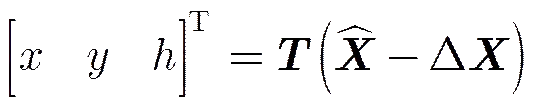
在多场景区域网联合定标中，设第(=1,2,,)块场景的待求解的干涉参数修正量为GCP点的数目为，该场景中第个GCP处的3维位置为、干涉参数初值为，则GCP点处的约束条件为

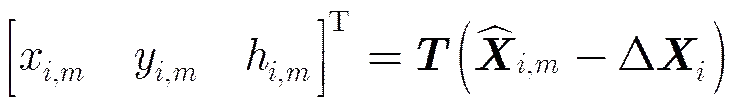
在联合定标中，同名点是指同一地物在两个邻接场景中所对应的两个像素点，因此两个场景中关于同名点3维位置的计算结果应当一致。设第块与第块场景相邻，并且该两场景之间有对同名点，则第对同名点处的约束方程可写为

(4)

联合定标相当于求解式(3)、式(4)所表征的方程组，从而获得各场景的干涉参数偏差，但其通常为非线性超定方程组，难以直接求解。传统的定标算法采用基于线性化误差近似的敏感度迭代算法，该算法在处理联合定标时首先将式(3)进行线性化近似，通过敏感度方程迭代求解参数修正量，其次通过同名点3维位置信息的传递实现式(4)所表征的同名点约束条件，其不足在于：线性化的近似会造成精度损失，并且联合定标的处理流程较为繁琐。

鉴于传统算法的不足，考虑采用最优化的方法求解式(3)、式(4)联立的方程组，即构造函数如下：

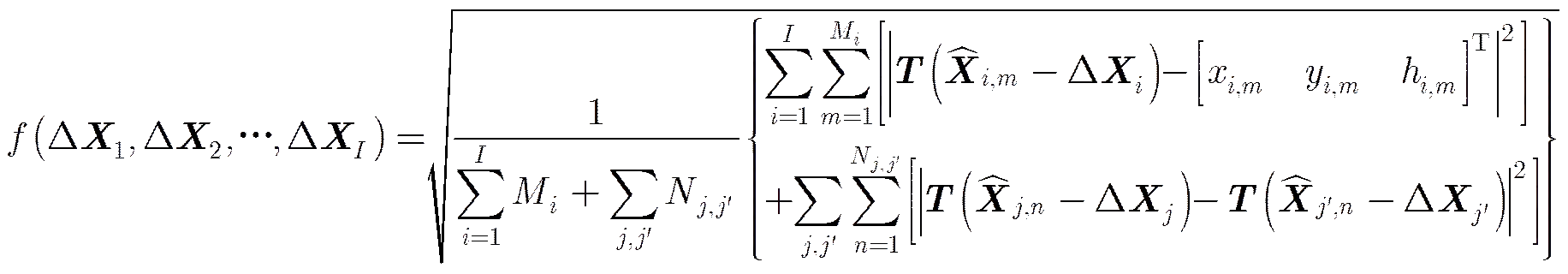
4 加权定标算法

鉴于随机误差等因素的存在，式(3)、式(4)中各方程的可信度并不完全一致，有必要区别对待各方程。于是考虑对各方程引入权值，将其转化为加权最优化模型进行求解。

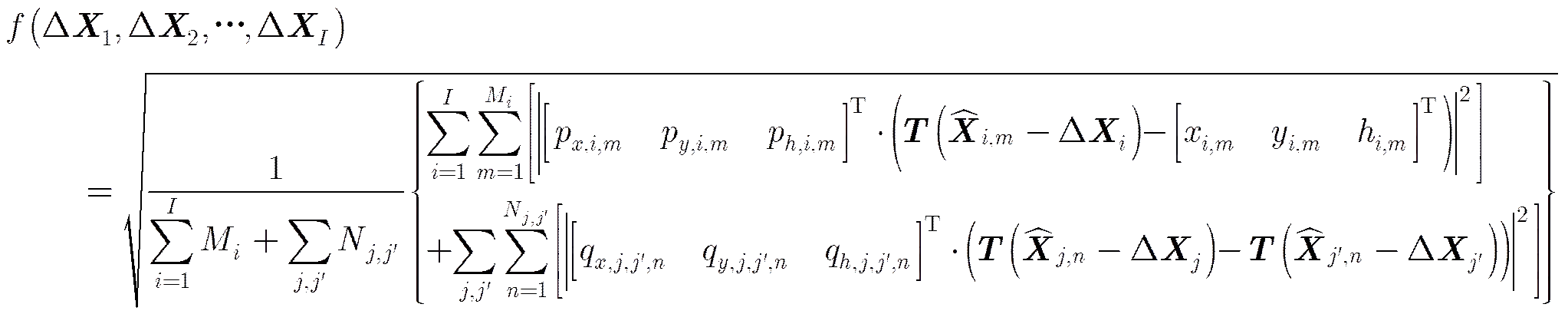
4.1依据相干系数加权

3维位置误差可由相位误差表征，相位误差可由相干系数表征，则相位噪声在各GCP点处引入的3维位置误差可表述如下：

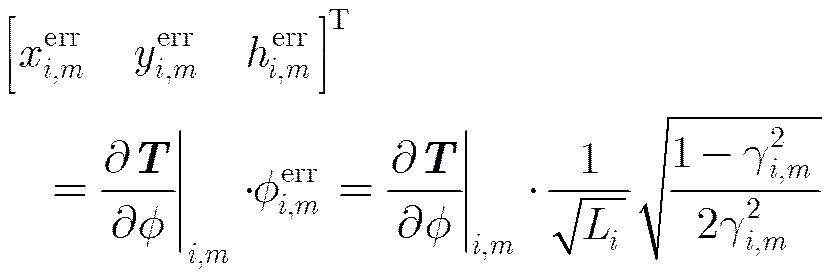
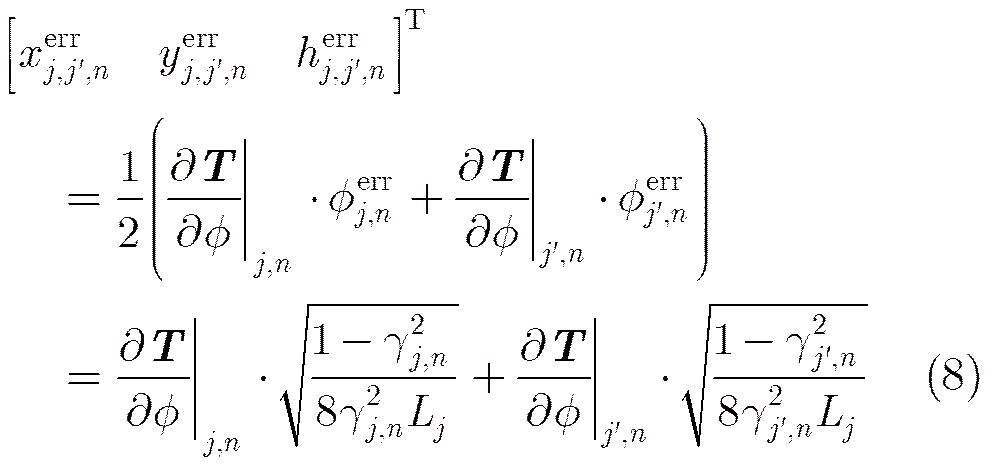
鉴于式(7)、式(8)所示的位置误差对式(3)、式(4)的贡献为线性关系，可以将权值设置为位置误差的反比例函数，以减弱误差的影响，即

(9)

4.2依据精度指标加权

在应用机载InSAR进行测绘作业时，某些制图产品关于高程精度与平面位置精度的指标要求不同，关于位置绝对精度与位置衔接性精度的指标要求也不同，因此在定标处理过程中有必要通过加权的方式来体现出对各种精度指标的不同要求。举例来说，基于InSAR的比例尺为1:50000的制图产品对高程精度的要求为5 m，对平面位置精度的要求为25 m。通常，为了保证拼接效果，制图产品对位置衔接性的精度要求会更高。所谓位置衔接性精度，是指相邻场景在拼接时的衔接误差，在定标时主要依赖TP点的约束方程进行衔接性保证。

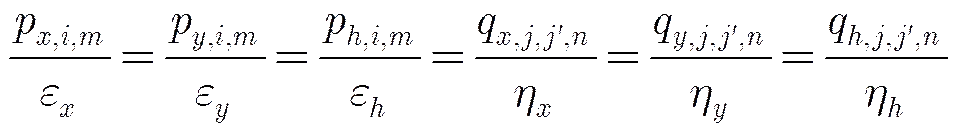
依据式(10)的要求，可将各权值设置如下：

(11)

4.3综合加权

加权的实质就是分配式(3)、式(4)中关于GCP和TP点3维位置的6组方程的比例系数。因此，当存在多种加权依据时，可将每一种依据对应的权值串联相乘，以获取最终权值，即

①河（沟）道防洪以保障人的生命安全为首要目的，10年一遇～20年一遇洪水淹没范围设为河（沟）道防洪范围，包括常水位河（沟）床和河滩地等，防洪范围内不应该有人居住的房屋。措施配置主要包括拆除违章建筑物、扩大防洪空间、护坡和防洪坝等，考虑河（沟）道两侧当地雨水排入河（沟）道的问题，防洪坝坝顶和护坡坡顶高程不高于外侧地面高程。采取生态的护岸形式，治理材料应主要考虑自然生态材料。

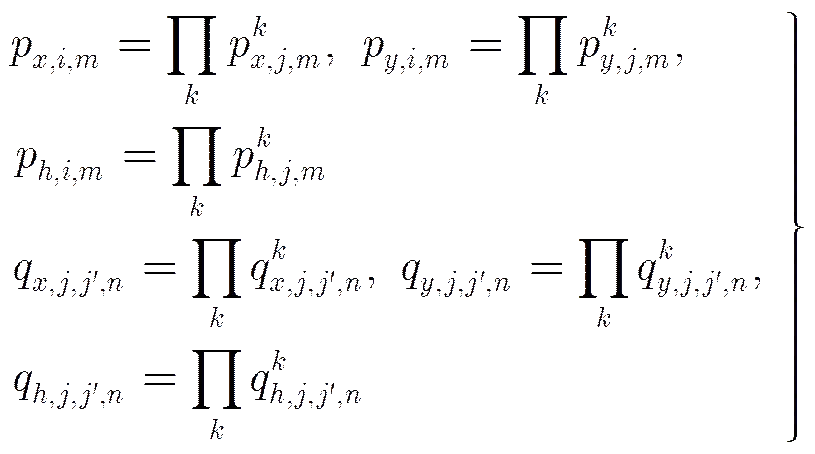
综上所述，鉴于随机相位误差的存在、各维精度指标的差异等因素，各GCP和TP点处的约束方程在定标中的地位和影响不同，因此有必要在定标过程中引入权值，下文的实验结果也显示加权后的定标精度能够得到提高。

5 区域网3维定位流程

在机载InSAR测图作业中，在获得已展开的干涉相位后，首先进行联合定标，以修正定位模型中的干涉参数；其次进行3维位置反演，即利用3维定位几何模型和定标后的参数，由干涉相位反演出3维位置(如图2所示)；最后进行各场景幅度图和DEM的拼接(如图3所示)，即在平面位置坐标网格下对各场景幅度图和DEM进行规则化重采样和拼接，以形成制图产品。在整个流程中，联合定标是关键的一步，其关系到制图产品的3维位置精度。

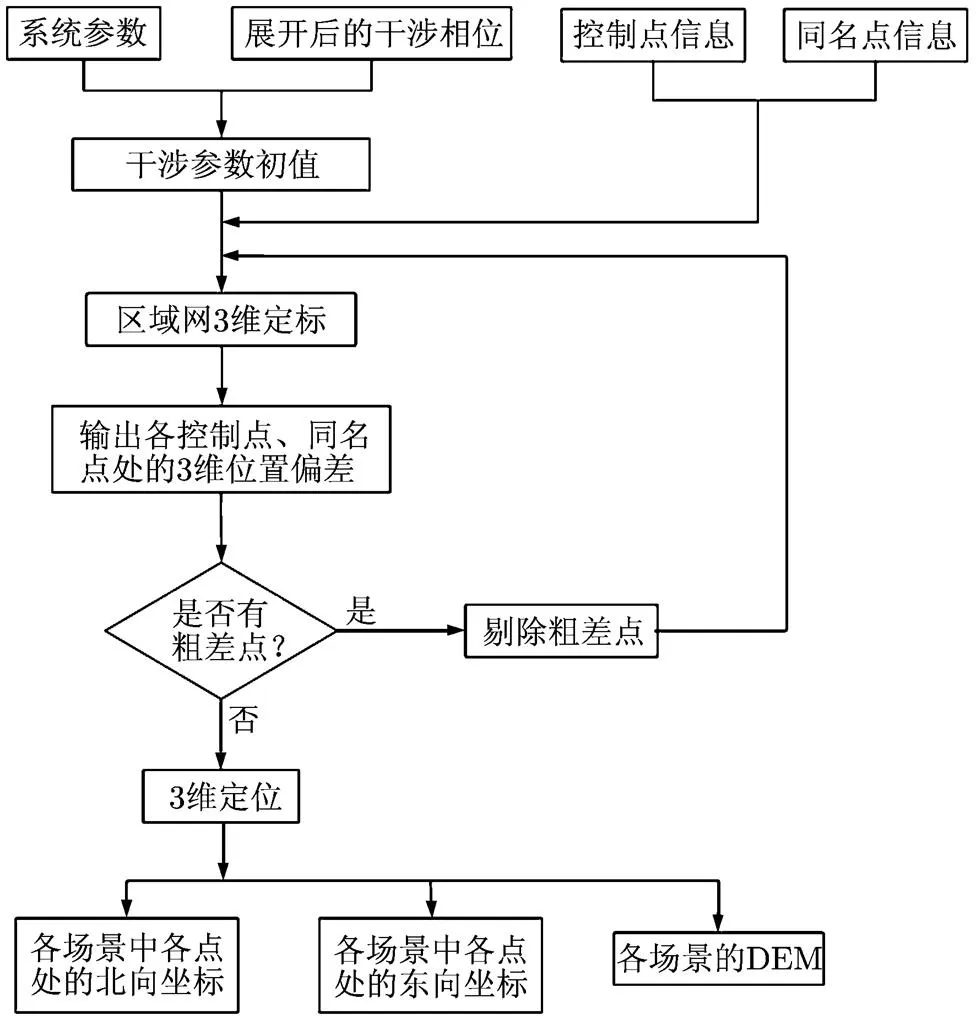
图2 机载InSAR区域网3维定位流程

6 实验结果与分析

本文选取了机载双天线InSAR实测数据对所提算法进行了验证，所选数据的斜距域SAR图像如图4所示，其基本参数为：载频9.6 GHz，信号带宽400 MHz，采样频率600 MHz，脉冲重复频率2000 Hz，基线长度2.3 m，基线倾角，平台高度3.3 km，平台速度100 m/s。对该数据按图2、图3所示的流程进行处理，所得正射DEM与正射幅度图的结果如图5所示。

图4所示的场景中，共布放有8个已知3维位置的角反射器，在联合定标中用作GCP点；另有80个在后期的野外控制测量中获知3维位置信息的点，用作检验点，以检验定标后的3维位置精度；各相邻场景之间共选取282对同名点，其中180对用于联合定标；另外102对同名点用作检查点，以检验联合定标后相邻场景之间的3维位置衔接性。在相邻场景之间选取同名点时，采用SIFT(Scale Invariant Feature Transformation)的方法进行匹配，并通过人机交互的方式进行检验筛选。

图4中的InSAR数据在经过联合定标后的3维位置精度如表1所示(高程、北向位置、东向位置的误差量级各不相同，主要是因为载机的真航向角的误差对高程反演无影响，对北向和东向定位的影响不相同)。其中，传统定标算法是指基于线性化误差近似的敏感度迭代算法，其首先对高程进行定标，其次在获取的DEM的基础上，再对平面位置进行定标；最优化3维联合定标是指按照式(5)所示的目标函数进行最优化处理的定标算法，其同时对目标的3维位置进行定标处理；加权最优化3维联合定标是指按照式(6)所示的目标函数和式(9)所示的权值进行加权最优化处理的定标算法，其同时对目标的3维位置进行定标处理。

表1各种定标算法精度的比较

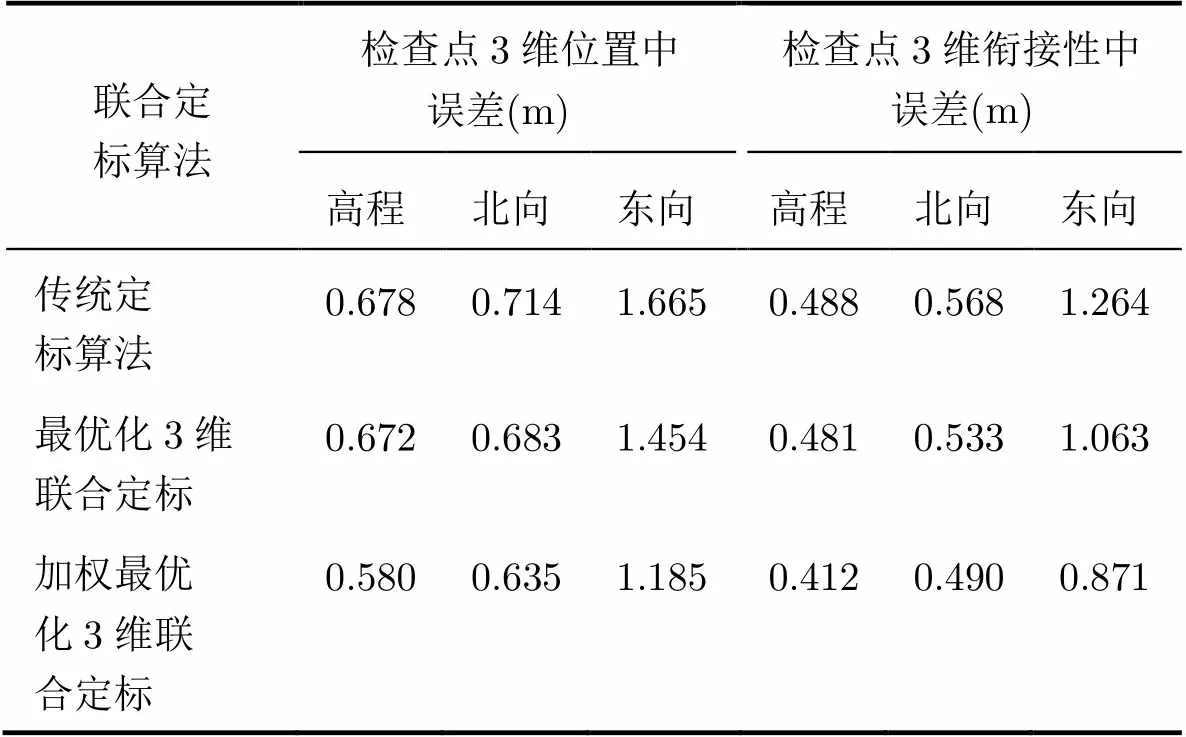
Tab. 1 RMS of the residuals after calibration using differentmethods

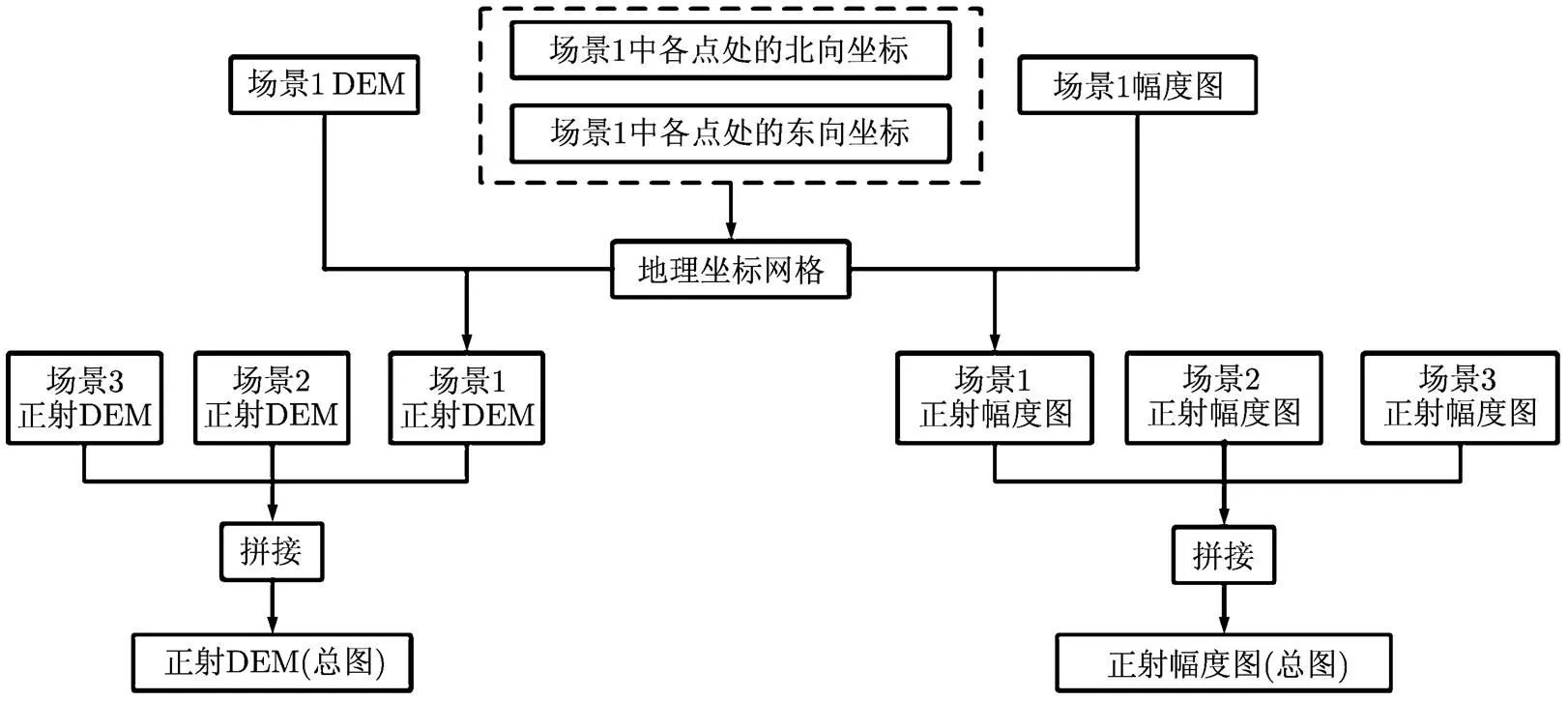
图3 机载InSAR多场景数据拼接流程

表1所示的实验结果显示：在高程精度方面，最优化3维联合定标算法与传统定标算法相当，而在平面位置精度方面则优于传统定标算法，究其原因，最优化3维联合定标算法将对高程和对平面位置的定标同时进行，不会造成高程误差在平面位置定位中的累积；合理加权能够进一步提高定标的3维位置精度和衔接性精度，究其原因，加权最优化定标顾及到了不同相干性、不同位置分布的控制点和同名点的权重差异。

图4 斜距域SAR图像

7 结束语

本文所提出的基于加权最优化模型的3维联合定标算法能够对目标的3维位置同时定标，且在稀少控制点条件下实现大区域多场景的3维定位。另外，本文算法为联合定标引入了权值，并且给出了权值的计算方法。相比于传统算法，本文所提算法在一定程度上改善了定标精度，并且在处理流程上更为简洁。

[1] Blacknell D, Freeman A, Quegan S,.. Geometric accuracy in airborne SAR images[J]., 1989, 25(2): 241-258.

[2] Mohr J J and Madsen S N. Geometric calibration of ERS satellite SAR images[J]., 2001, 39(4): 842-850.

[3] Paul Siqueira, Bruce Chapman, and Greg McGarragh. The coregistration, calibration, and interpretation of multiseason JERS-1 SAR data over South America[J]., 2004, 90(4): 536-550.

[4] Rosen P A, Hensley S, Joughin I R,.. Synthetic aperture radar interferometry[J]., 2000, 88(3): 333-382.

[5] Crosetto M. Calibration and validation of SAR interferometry for DEM generation[J].&, 2002, 57(3): 213-227.

[6] Madsen S N, Zebker H A, and Martin J. Topographic mapping using radar interferometry: processing techniques[J]., 1993, 31(1): 246-256.

[7] Dall J. Cross-calibration of interferometric SAR Data[J].-,, 2003, 150(3): 177-183.

[8] Dall J, Grinder-Pesolution J, and Madsen S N. Calibration of a high resolution airborne 3-D SAR[C]. IEEE Geoscience and Remote Sesing Symposium, Singapore, August 1997: 1018-1021.

[9] Mao Yong-fei, Xiang Mao-sheng, Wei Li-deng,.. The mathematic model of multipath error in airborne interferometric SAR system[C]. IEEE Geoscience and Remote Sesing Symposium, Honolulu, USA, July 2010: 2904-2907.

[10] Kobayash Y, Sarabandi K, Pierce L,.. An evaluation of the JPL TOPSAR for extracting tree heights[J]., 2000, 38(6): 2446-2454.

[11] D’Aria D, Ferretti A, Guarnieri A M,.. SAR calibration aided by permanent scatterers[J]., 2010, 48(4): 2076-2083.

[12] Bräutigam B, González J H, Schwerdt M,.. TerraSAR-X instrument calibration results and extension for TanDEM- X[J]., 2010, 48(2): 702-715.

[13] Freeman A. SAR calibration: an overview[J]., 1992, 30(6): 1107-1121.

[14] Mao Yong-fei, Xiang Mao-sheng, Wei Li-deng,.. A weighted calibration method of interferometric SAR data[C]. IEEE Geoscience and Remote Sesing Symposium, Vancouver, Canada, July 2011: 2555-2557.

[15] 毛永飞, 向茂生, 韦立登. 一种机载干涉SAR区域网平面定位算法[J]. 电子与信息学报, 2012, 34(1): 166-171.

Mao Yong-fei, Xiang Mao-sheng, and Wei Li-deng. A block positioning method for airborne InSAR system[J].&, 2012, 34(1): 166-171.

[16] Zebker H A, Werner C L, Rosen P A,.. Accuracy of topographic maps derived from ERS-1 interferometric radar[J]., 1994, 32(4): 822-836.

[17] Moreira J, Schwabisch M, and Fomaro G. X-SAR interferometry: first results[J]., 1995, 33(4): 950-956.

[18] 毛永飞, 向茂生. 基于加权最优化模型的机载InSAR 联合定标算法[J]. 电子与信息学报, 2011, 33(12): 2819-2824.

Mao Yong-fei and Xiang Mao-sheng. Joint calibration of airborne interferometric SAR data using weighted optimization method[J].&, 2011, 33(12): 2819-2824.

[19] Touzi R and Lopes A. Statistics of the Stokes parameters and the complex coherence parameters in one-look and multilook speckle fields[J]., 1996, 34(2): 519-531.

[20] Lourenco M, Barreto J P, and Malti A. Feature detection and matching in images with radial distortion[C]. IEEE International Conference on Robotics and Automation, Anchorage, Alaska, USA, 2010: 1028-1034.

Joint Three-dimensional Location Algorithm for Airborne Interferometric SAR System

Mao Yong-feiWang Xiao-jieXiang Mao-sheng

(Beijing Institute of Spacecraft System Engineering, Beijing100094, China)(Beijing Institute of System Engineering, Beijing 100101, China)(National Key Laboratory of Science and Technology on Microwave Imaging, Institute of Electronics,Chinese Academy of Sciences, Beijing 100190, China)

Joint three-dimensional location algorithms aim to simultaneously obtain the north, east, and height coordinates of each pixel in several adjacent Interferometric Synthetic Aperture Radar (InSAR) scenes. Joint calibration is a key procedure used to achieve an accurate three-dimensional location. It can ensure the continuity of three-dimensional locations among adjacent scenes, and achieve the location of large areas with few Ground Control Points (GCPs) using Tie Points (TPs). In this paper, a new joint calibration algorithm for airborne interferometric SAR that simultaneously calibrates north, east, and height coordinates is proposed. It employs a weighted optimization method to carry out calibration, and introduces weights to calibration to discriminate GCPs and TPs with different coherences and locations. The experimental results for airborne InSAR data show that the three-dimensional location accuracy obtained using the proposed calibration algorithm is better than that obtained using the traditional method.

Synthetic Aperture Radar (SAR); Interferometric; Joint calibration; Three-dimensional location; Weighted optimization

TN959.73

A

2095-283X(2013)01-0060-08

10.3724/SP.J.1300.2013.20107

毛永飞(1983-)，男，毕业于中国科学院电子学研究所，博士，现任职于北京空间飞行器总体设计部，研究方向为合成孔径雷达(SAR)系统设计、成像、运动补偿、干涉、定标与制图处理；雷达的系统设计、系统校准与数据处理。

2012-12-31收到，2013-01-21改回；2013-01-28网络优先出版

国家863计划(2007AA120302)和国家973计划(2009CB724003)资助课题

毛永飞 maoyongfei@gmail.com