危险品运输中的可控风险最大流算法

毛华，赵小娜

（河北大学 数学与计算机学院，河北 保定 071002）

据统计，中国每年道路运输危险物2×108t左右，易燃易爆油品类达108t.危险品运输一旦发生事故，具有伤亡人数多、环境污染严重等危害.如果对危险处理不妥，将会造成长远的危害.学者们一直在从事危险品运输路线的选择和优化问题［1－10］，目前研究重点从事后处理向事前预防过渡［11］.通常的算法大多是从线性规划和概率出发，把影响因素逐一进行考虑，算法繁琐，故本文把各种可能造成风险的因素统一为一个风险值，用寻找最大风险路的算法，实现可控风险最大流算法.

1 预备知识

引进有关风险网络的基本知识.

定义1［12－14］1）最短路Dijkstra算法原理：若路P＝νsν1…νk－1νk是从νs到νk的最短路，则P′＝νsν1…νk－1必定是从νs到νk－1的最短路，基于这一原理，算法得出网络G 中指定顶点νs到其余各点的最短路.2）求最小费用ν0流的负费用圈算法思路：①使用Dinic最大流算法，求出网络G 中流量为ν0的可行流；②使用最短路算法，寻找增量网络N（f）中的负费用有向圈，并沿该圈进行增流，从而使可行流的费用降低.

给出如下定义和算法.

定义2 风险矩阵：M（ω）＝（ωij）n×n，其中ωij为有向边νiνj的风险值.若νi到νj无路，则ωij＝－∞；ωii＝－∞.增量矩阵：M（t）＝（tij）n×n，其中tij为有向边νiνj的可增流量值.若νi到νj无路，则tij＝∞；tii＝∞.

Dinic算法［12－14］

Begin

while G 中存在增广路do

begin

利用最短路算法，在G 中寻找一条增广路P；

δ＝min｛tij｜（i，j）∈P｝；

沿P 增流δ；

更新G；

end；

End

2 算法

2.1 算法

算法1给出求νs到νt最大风险路.算法2在算法1的基础上，给出危险品运输中已知可控风险ω0，进而得到最大流.

算法1 最大风险路算法

Begin

Pf＝Φ；

if G 中存在νs－νt路P；

在G 中找到P1，满足：

ω（P1）＝max｛ω（Pi），Pi∈P｝；

Pf＝P1；

End

算法2 求可控风险ω0的最大流算法

Begin

利用算法1，求得G 的一条νs－νt有向路P 及ω（P）；

while ω（P）＞ω0do

begin

for （i，j）∈P；

θ（eij）＝max｛ω（P）｝；

在G 中沿P 去掉eij；

更新G；

end；

在网络G 中运行Dinic算法；

End

2.2 算法复杂性分析和比较

文中ν和ε 分别表示网络G 顶点的总个数和边的总数；ωP1表示最大风险路P1的风险值，ω0表示事先给定的风险值，cmax和ωmax表示的是网络G 中所有弧上容量的最大值和风险值的最大值.

定理1 1）求可控风险ω0的最大流算法的复杂度为O（ν2·ε·（ωP1－ω0））；2）著名的求最小费用ν0流的负费用圈算法的复杂度为O（ν3·ε·cmax·ωmax）；3）2个算法进行比较，1）比2）的复杂度低.

证明 1）第1步用最大风险路算法，有νs到νt最大风险路P1，复杂度为O（ν2），而该步风险值至多循环（ωP1－ω0）次，因此该步的复杂度为O（ν2·（ωP1－ω0））；第2步调用Dinic算法，求更新后网络G 的最大流，该步复杂度为O（ν2·ε）；从而算法总的复杂度为O（ν2·（ωP1－ω0）＋ν2·ε）＝O（ν2·ε·（ωP1－ω0））.

2）证明详见参考文献［14］.

3）网络G 中最大风险路P1的风险值ωP1不会超过（ν－1）·ωmax，从而

ωP1－ω0≤（ν－1）·ωmax－ω0＜ν·ωmax＜ν·ωmax·cmax，即ν2·ε·（ωP1－ω0）＜ν3·ε·cmax·ωmax.

算法1是改进最短路Dijkstra算法得到的.算法2是改进求最小费用ν0流的负费用圈算法［14］得到的.通过此处算法和著名算法的分析和比较，可以得到如下几点：

1）最大风险路算法和最短路算法的复杂性都是O（ν2）；但最大风险路算法不是最短路算法的对偶，在比较风险值大小时，最短路需将该顶点的所有发量进行比较，而最大风险路算法不必考虑到收点的风险值.

2）求最小费用ν0流的负费用圈算法通过增量网络寻找负费用有向圈，运用最短路算法时，复杂度为O（ν3）；而求可控风险ω0的最大流算法，运用最大风险路算法时，风险值不产生负值，复杂度为O（ν2）.

3）求最小费用ν0流的负费用圈算法中网络G 始终是保持不变的；而求可控风险ω0的最大流算法通过寻找最大风险路，把不满足条件的弧逐一删去，从而使网络G 简化，在增流过程中，带来了很大的方便.

由上述几点可知，此处求可控风险ω0的最大流算法复杂度低，应用简单、方便.

3 算法实例

本节通过实例说明上一节算法是如何实现的.

某核电站要运输一批核废料，选择一条从出发点到存储点的最优路线.把运输路线抽象成网络G＝（V，A，C，ω），如图1所示，νs表示产生核废料的地点；νt表示核废料的存储点；ν1，ν2，ν3，ν4表示2条及2条以上公路的交汇处，弧上第1个数字为容量，第2个数字为风险值.下面运用求可控风险ω0的最大流算法求网络G 中风险ω0为10的最大流.

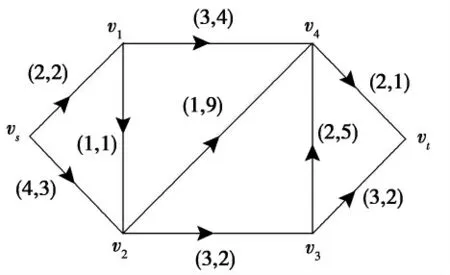
图1 网络G＝（V，A，C，ω）Fig.1 The network G＝（V，A，C，ω）

由算法2作出风险矩阵：

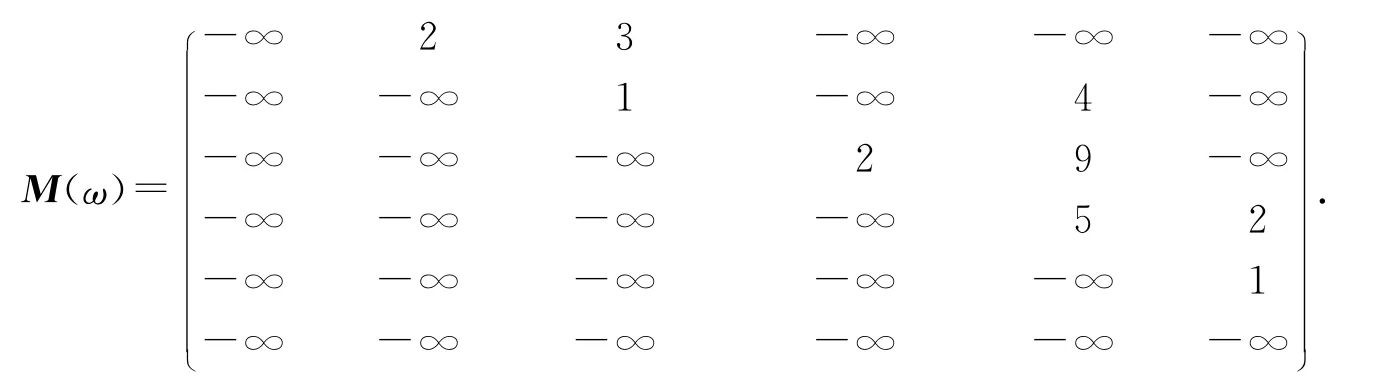
在M（ω）中运行算法1，得到G 的一条最大风险νs－νt有向路P1:νsν2ν4νt，及ωP1＝13＞ω0，此时θ（ν2ν4）＝9，沿P1去掉弧ν2ν4，更新网络G，如图2所示.此时，作出如下新的风险矩阵：

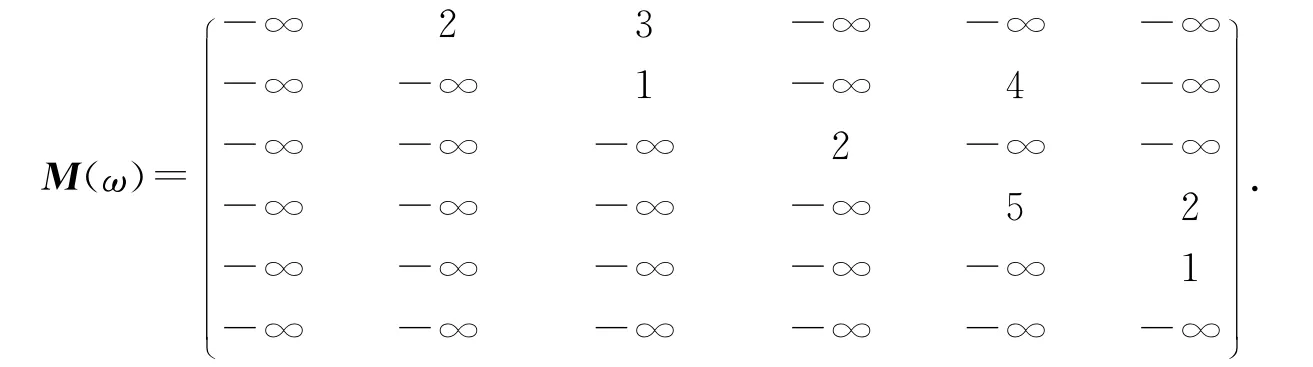
运行算法1，得到G 的一条最大风险νs－νt有向路P1:νsν2ν3ν4νt，及ωP1＝11＞ω0，此时θ（ν3ν4）＝5，沿P1去掉弧ν3ν4，更新网络G，如图3所示.此时，作出如下新的风险矩阵：

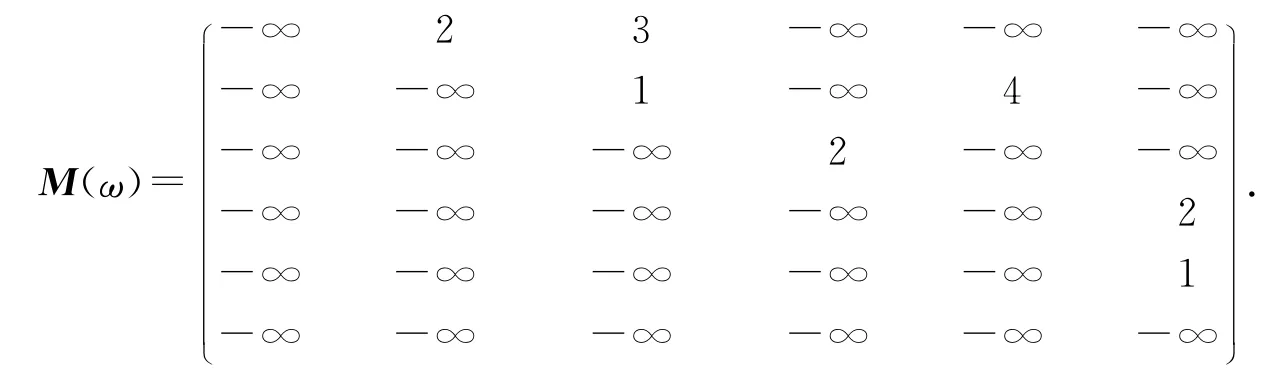
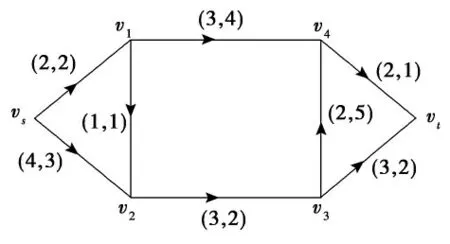
图2 沿P 去掉弧ν2ν4 更新后的网络GFig.2 Updated network G by remoνing arc ofν2ν4based on P

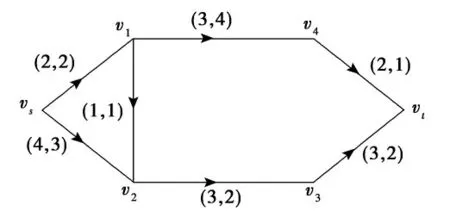
图3 沿P 去掉弧ν3ν4 更新后的网络GFig.3 Updated network Gby removing arc ofν3ν4based on P

运行算法1，得到G 的一条最大风险νs－νt有向路P1:νsν2ν3νt，此时ωP1＝7＜ω0，结束.在图3中，运行Dinic算法，此时增量矩阵为：

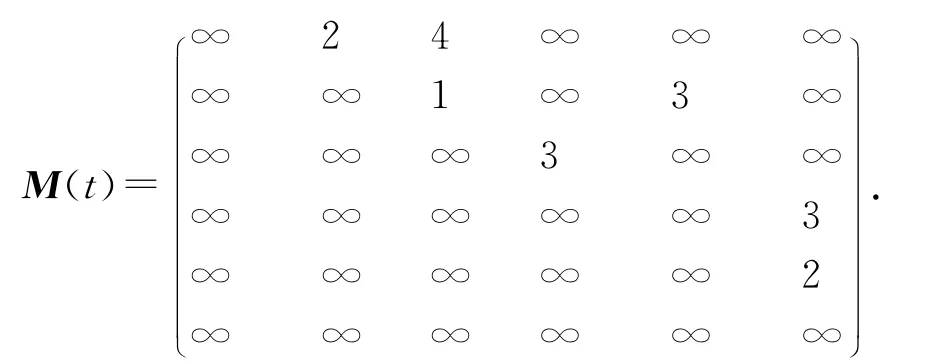
在M（t）中运行最短路Dijkstra算法［12－14］，得到

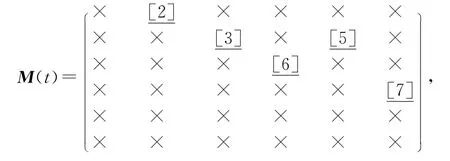
即一条νs－νt增广路P:νsν1ν4νt，沿P 增流δ＝2后，如图4所示.此时，得到如下新的增量矩阵M（t），弧上括号外数字为流值，括号内数字为可增流量值.

运行最短路Dijkstra算法，得到一条νs－νt增广路P:νsν2ν3νt，沿P 增流δ＝3后，如图5所示.此时，得到新的增量矩阵：

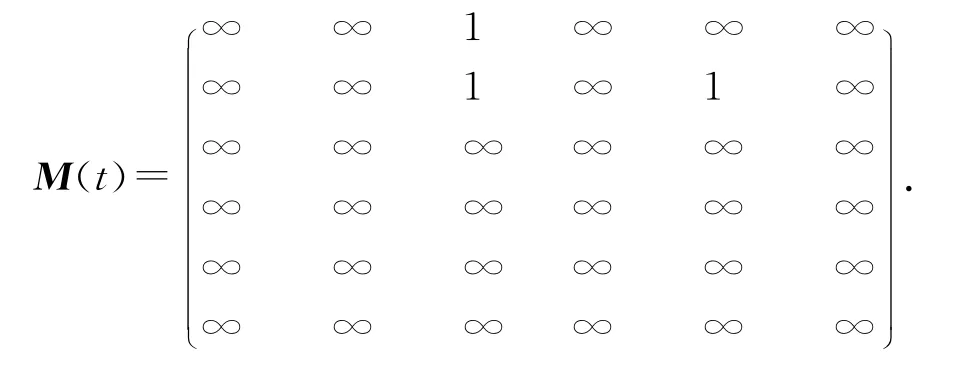
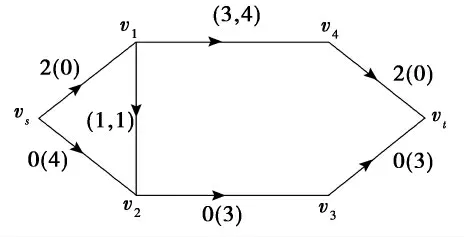
图4 沿P 增流后的网络GFig.4 Incremented flow of network Gbased on P

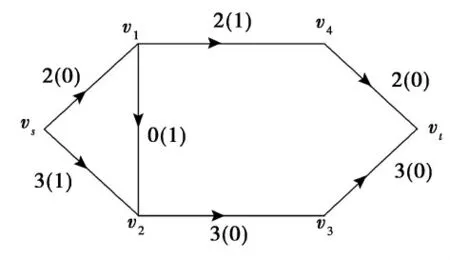
图5 沿P 增流后的网络GFig.5 Network Gafter incrementing flow based on P

运行最短路Dijkstra算法，得到νs－νt已无增广路，即网络G 已达到最大流5.

关于本例的算法复杂性分析如下：

本例顶点数ν＝6，风险值ω0＝10.

1）风险矩阵M（ω）＝（ωij）n×n，用最大风险路算法，得ωP1＜ω0的2条最大风险路P1，更新2次网络G，因此该步的复杂度为ν2·（ωP1－ω0）＝72.

2）在最新的网络G 中，用Dinic算法［14］寻找网络G 的最大流，此时ε＝7，该步的复杂度为ν2·ε＝252.本例可控风险ω0的最大流算法的复杂度为ν3·ε·（ωp1－ω0）＝504.而本例最小费用ν0流的负费用圈算法的复杂度为69 984.

由此知，该算法与最小费用ν0流的负费用圈算法相比较，不仅复杂性低，而且可简化网络.从本例可以看出，本文的算法简单易行、有效性高.

［1］ MIAOU S P，CHIN S M.Computing k－shortest path for spent nuclear fuel highway transportation［J］.European Journal of Operational Research，1991，53：64－80.

［2］ KARA B Y，ERKUT E，VETER V.Accurate calculation of hazardous materials transport risk［J］.Operations Research Letters，2003，31：285－292.

［3］ BUBBICO R，CAVE S D，MAZZAROTTA B.Risk analysis for road and rail transport of hazardous materials：a simplified approach［J］.Journal of Loss Prevention in the Process Industries，2004，17：477－482.

［4］ 毛华，赵小娜，毛晓亮.危险品运输中的最小风险最大流算法［J］.计算机工程，2012，38（9）：268－270.MAO Hua，ZHAO Xiaona，MAO Xiaoliang.Minimal risk and maximal flow algorithm in hazardous materials transportation［J］.Computer Engineering，2012，38（9）：268－270.

［5］ 毛华，俞珊珊.任意基数集上的拟阵的约束［J］.河北大学学报：自然科学版，2009，29（1）：22－24.MAO Hua，YU Shanshan.Restriction of matroids of arbitrary cardinality［J］.Journal of Hebei University：Natural Science Edition，2009，29（1）：22－24.

［6］ 任常兴，吴宗之.危险品道路运输选线问题分析［J］.安全与环境学报，2006，6（2）：84－88.REN Changxing，WU Zongzhi.On route－choice analysis of hazardous materials transportation［J］.Journal of Safety and Environment，2006，6（2）：84－88.

［7］ 谢凡荣，贾仁安.供给总量限定需求区间约束型运输问题－时限费用优化模型与算法［J］.运筹与管理，2008，17（1）：42－47.XIE Fanrong，JIA Renan.The transportaion problem with supply amount specified and demand interval constraint－models and algorithms for optimization on time limit and cost［J］.Operations Research and Management Science，2008，17（1）：42－47.

［8］ 毛华，毛晓亮，李斌.网络最大流部分割矩阵算法［J］.计算机科学，2011，38（12）：229－231.MAO Hua，MAO Xiaoliang，LI Bin.Partial cut algorithm for maximum－flow of network［J］.Computer Science，2011，38（12）：229－231.

［9］ 易玉枚，廖可兵，张佐钊，等.危险化学品物流网络选址－运输优化研究［J］.中国安全科学学报，2011，21（6）：135－140.YI Yumei，LIAO Kebing，ZHANG Zuozhao，et al.Study on location－transportation optimization for hazardous material logistics network［J］.China Safety Science Journal，2011，21（6）：135－140.

［10］ 毛华，谢利伟.全弧搜索广义拟阵的构造［J］.河北大学学报：自然科学版，2010，30（2）：133－136.MAO Hua，XIE Liwei.Construction of searching are greedoids［J］.Journal of Hebei University：Natural Science Edition，2010，30（2）：133－136.

［11］ 严虎.危险品公路运输安全管理现状及探究［J］.北华航天工业学院学报，2011，21（4）：17－19.YAN Hu.Status and investigation on highway transportation safety management of hazardous materials［J］.Journal of North China Institute of Aerospace Engineering，2011，21（4）：17－19.

［12］ BONDY J A，MURTY U S R.Graph theory with applications［M］.New York：Elsevier Science Publishing Corporation，1976.

［13］ BONDY J A，MURTY U S R.Graph theory［M］.Berlin：Springer，2008.

［14］ 高随祥.图论与网络流理论［M］.北京：高等教育出版社，2009.