一种新型并串联稳定平台运动学分析与实验研究

王立玲，王洪瑞，肖金壮，刘秀玲，薛瑞静

（河北大学 电子信息工程学院，河北 保定 071002）

稳定平台能隔离载体（导弹、飞机、战车、舰船）扰动，不断测量平台姿态和位置的变化，精确保持动态姿态基准.国防武器装备水平的发展，对装备的快速反应、稳定瞄准、跟踪和打击能力提出了更高的要求，因而对高精度稳定跟踪平台的需求变得更为迫切［1－3］.现有的稳定平台基本上都是串联结构，由于本体过重和驱动力小，使得其在大负载场时应用存在难于控制的问题.因此，承载大、具有大工作空间和高动态响应的并联稳定平台成为热点问题，受到学者的普遍重视.但是，由于少自由度并联机器人机构运动学、动力学分析的复杂性和理论研究的滞后，限制了采用这类机构作为新型的稳定平台机构的发展.

对球面并联机构的研究大多集中在球面3自由度并联机器人机构上.例如Gosselin等系统地研究了角台型球面并联机构，并在1994年成功研制了称为“灵巧眼”的摄像机自动定位装置［4－5］，球面2－DOF机器人机构是所有转动轴线相交于一点的空间结构，其运动为绕定点的转动.由于制造相对简单经济，结构紧凑，特别适用于空间姿态变化的地方［6－7］.本文对并串联型稳定平台的机构和运动特性等方面进行系统深入的研究，根据机构几何特点，利用向量法和欧拉角法建立稳定平台机构运动学模型；设计了3－DOF稳定平台实验装置，将实验结果与理论计算进行对比.结果表明，所建立的并串联3－DOF稳定平台运动学模型准确有效.

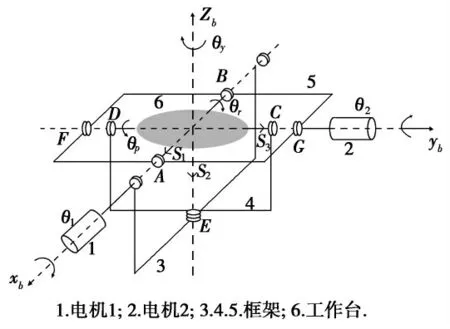
图1 2－DOF球面并联机构Fig.1 2－DOF spatial gimbal mechanism

1 机构运动学分析

1.1 机构说明

3－DOF并串联稳定平台由如图1 所示2－DOF 球面并联机构和串联在其上的转动副构成.2－DOF 球面并联机构为空间5杆机构，运动副均为转动副，所有轴线皆汇交于一点O，2电机轴互相垂直.2－DOF 球面并联机构运动平台做围绕球心O 的转动.电机3固连在2－DOF机构的运动平台上，电机3的轴线垂直于该工作平台.

1.2 2－DOF球面并联机构运动学分析

描述基坐标系Ob－xbybzb，xb与电机1轴线一致，yb与电机2轴线一致，zb由右手螺旋法确定，动坐标系Om－xmymzm，xm，ym轴与工作台OA，OC 方向一致，zm由右手螺旋法则确定，S1为沿OmA 的单位矢量，S2沿OE 的单位矢量，S3沿OC 的单位矢量.2－DOF球面并联机构是纯转动机构，机构输入为电机输出转角θ1、θ2，机构输出为绕xb轴的滚转角θr，绕yb轴旋转为俯仰角θp.

1.2.1 由θ1、θ2确定工作台姿态矩阵

根据机构特点，电机2通过框架5直接驱动工作台，所以当电机2转过θ2时，S1向量为

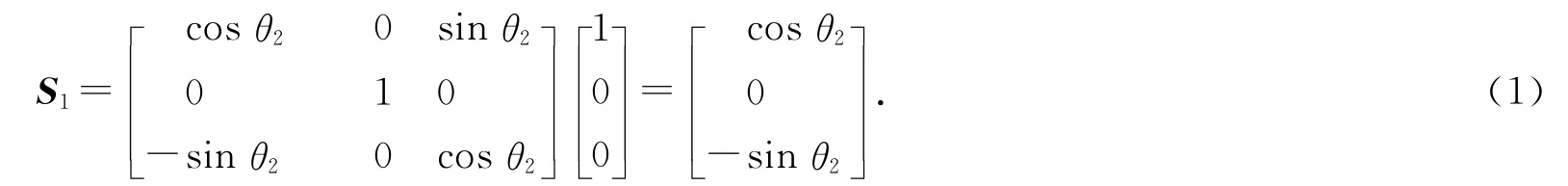
当电机1转过θ1，向量S1不变，向量

由机构几何特点，向量S3既垂直于向量S1，也垂直于向量S2，向量S1，S2，S3满足右手系

其中d＝｜S1×S2｜，则

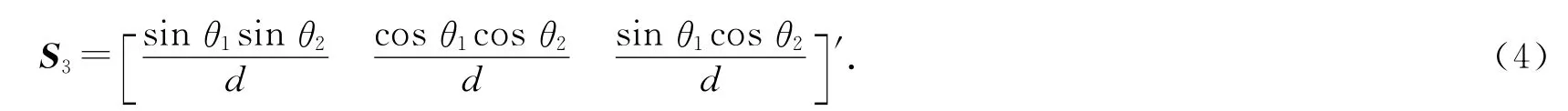
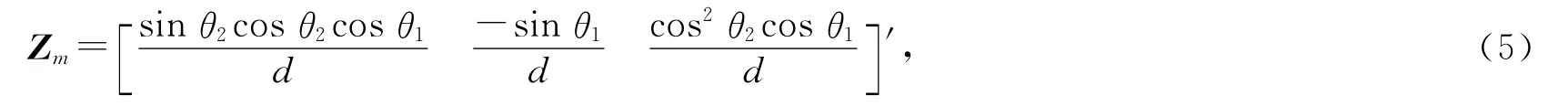
则由电机输入角θ1，θ2确定的上平台姿态矩阵

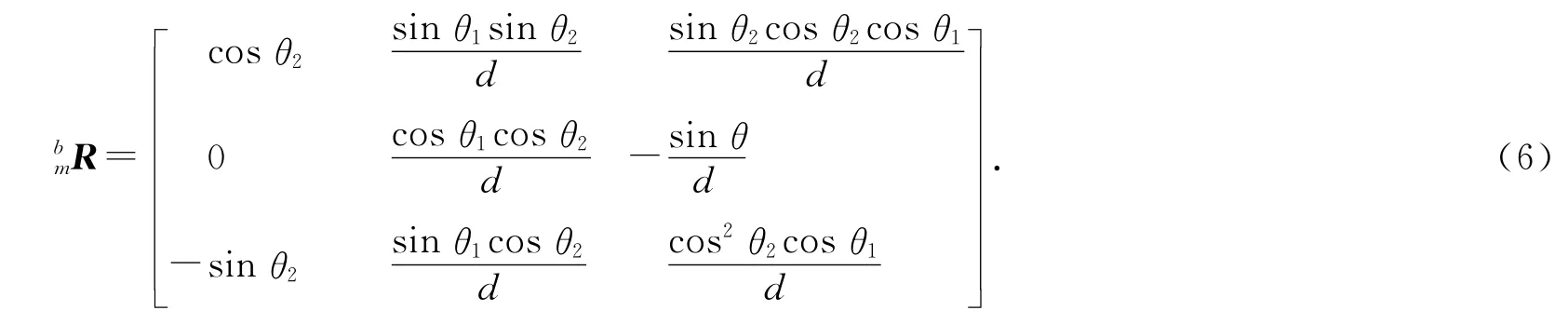
1.2.2 根据θr，θp确定工作台姿态矩阵

电机2直接驱动工作台绕Y 轴旋转，电机1驱动框架1，框架1与框架2通过转动副连接，框架2带动工作台绕Xm轴旋转.根据工作台可逆性原理，有工作台姿态矩阵为

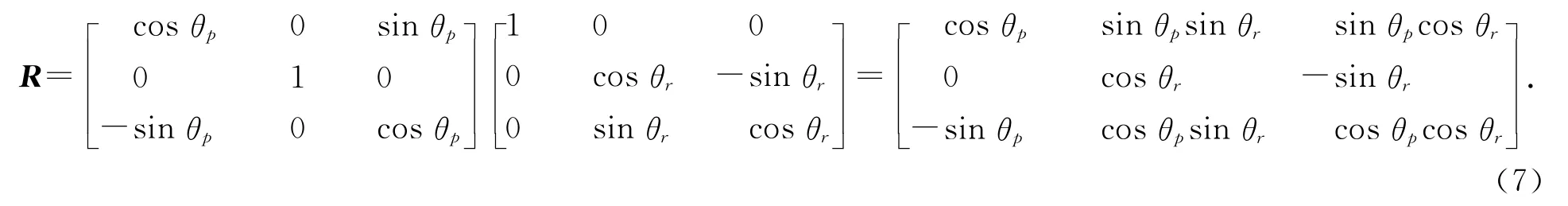
由式（6），（7）相等有

同理根据式（6），（7）相等可以推导2－DOF逆运动

实际工作平台输出转角－30°≤θr≤30°，－30°≤θp≤30°，由式（8），（9）可以推导出电机1和电机2的输入范围，电机2输入θ2范围和工作台输出的俯仰角θp是一致的，所以－30°≤θ2≤30°.因式（9）是单调增函数，当取最大时（θp＝0，θr＝30°），电机1的输入－30°≤θ1≤30°.

1.3 3－DOF并串联稳定平台雅可比矩阵

3－DOF并串联稳定平台中绕z轴转动的自由度由电机3独立控制，串联在2－DOF球面并联机构上，所以电机3的输入θ3相当于绕Z 轴的输入θy（θy为偏转角），即

根据式（8），（9），（12）有

其中J 为3－DOF并串联稳定平台雅可比矩阵

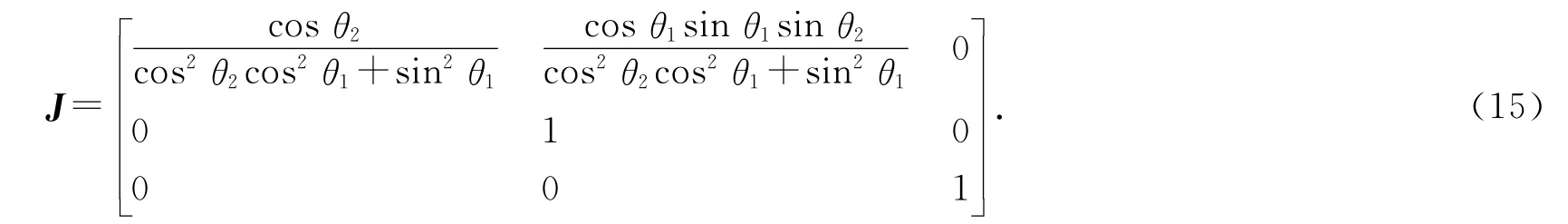
2 实验及结果分析

2.1 3－DOF并串联稳定平台实验装置

研制开发的3－DOF并串联稳定平台系统如图2所示，系统检测装置有2轴水平倾角传感器，用来检测工作台横滚角和俯仰角，有2个检测工作台绕X 轴和绕Y 轴旋转角速率的光纤陀螺仪，2－DOF球面并联机构分别由2个直流电机通过平行四边形连杆驱动，串联其上的工作台由电机直接驱动做360°×n周期运动.

图2 3－DOF并串联稳定平台系统Fig.2 Overview of the 3－DOF parallel－series platform

2.2 结果与分析

实验编程软件采用在Matlab软件中嵌入Canada Quanser公司QuaRC的方式实现.在程序中让电机2分别输入0，15°，27°时，通过倾角传感器的2模拟输出量采集平台输出转角，图3为实际输入输出之间曲线，图4－6为根据前面理论推导出的在电机2分别输入0，15°，27°时，电机1输入与工作台滚转角输出的理论曲线.

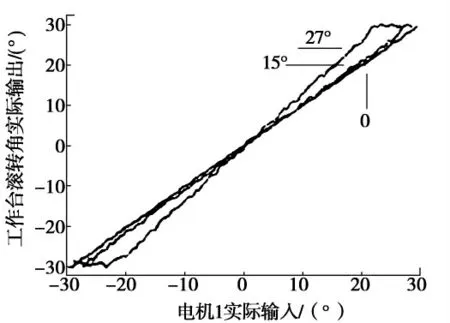
图3 实验结果Fig.3 Expriment result

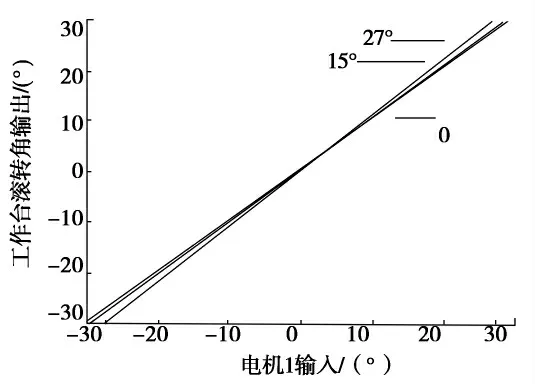
图4 理论推导结果Fig.4 Theoretical result

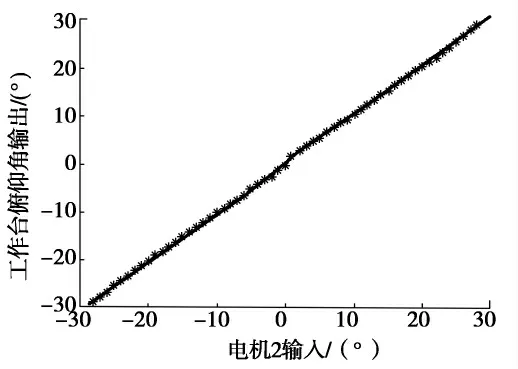
图5 理论推导与实验结果Fig.5 Theoretical result and expriment result

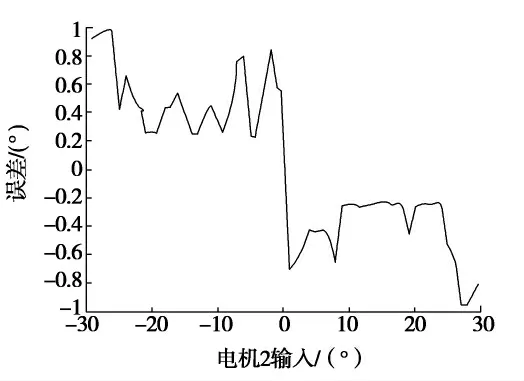
图6 绝对误差结果Fig.6 Absolute tolerance analysis

从图3，4可以看出，理论推导的运行学模型和实际平台模型是一致的.从平台逆运行得知，在电机2输入θp为0时，电机1的输入与平台输出是一致的，即θ1＝θr，电机1的输入－30°～30°；当电机2的输入θp是±15°时，θr最大输出是30°，所以电机1输入θ1－29°～29°；当电机2输入θp是－29°～29°时，θr最大输出是30°，所以电机1输入是－27°～27°.从图4中可以看出当电机2输入不同角度时，电机2的输入越大（工作台俯仰角越大），对工作台输出的横滚角输出影响越大.

从图3可以看出在电机2输入为27°，电机1在输入±24°附近时，出现横滚角接近最大值30°，即工作台在此情况下的最大输入，系统出现奇异点；在电机2输入为15°，电机1输入±28°附近时，出现横滚角接近最大值30°，即工作台在此情况下的最大输入，系统出现奇异点；在电机2输入为0，电机1输入±30°附近时，出现横滚角接近最大值30°，即工作台在此情况下的最大输入，系统出现奇异点.这和理论推导电机1输入范围是一致.

由式（3）得知，电机1输入与工作台俯仰输出一致，图5是在电机1输入20°时，电机2理论输出与实际输出曲线，从图中明显看出理论推导与实际一致.从曲线可以看出在0和±30°附近误差明显偏大，这是由于在传感器检测边缘，检测精度偏低［8］，并且在±30°时工作台输出最大值，容易出现奇异点.在图6误差曲线中间和两侧误差明显增大，也证实误差理论变化的特点.

3 结论

详细分析了3－DOF并串联稳定平台的工作原理，建立了稳定平台的基坐标和动坐标，运用向量法和欧拉角法推导出运动学模型和雅克比矩阵.通过实验测试表明工作台俯仰是独立的不受其他输入影响，工作台横滚角输出受工作的俯仰角影响，俯仰角度越大影响越大.这与理论推导完全一致.由于工作台方位角是由串联在俯仰和横滚上的电机独立控制的，所以方位角的精度由检测精度和控制精度决定.此机构工作空间对称、范围大，能够承受重载，是一种理想的稳定平台机构.

［1］ HILKERT J M.Inertially stabilized platform technology［J］.IEEE Control Systems Magazine，2008，1：26－46.

［2］ MOKBEL H F，LÜ Qiongying，ROSHDY Amr A，et al.Modeling and optimizatin of electro－optical dual axis inertially stabilized platform［Z］.2012International Conference on Optoelectroniss and Micrelectronics，Changchun：2012.

［3］ DENG Ke，CONG Shuang，SHEN Honghai.Control strategies and error compensation methods of high precision gyro stabilized platform［Z］.30th Chinese Control Conference，Yantai：2011.

［4］ 罗二娟，牟德军，赵铁石，等.耦合型三自由度并联稳定平台机构及其运动特征［J］.机器人，2010，32（5）：681－687.LUO Erjuan，MU Dejun，ZHAO Tieshi，et al.A 3－DOF coupling parallel mechanism for stabilized platform and its motion characteristics［J］.Robot，2010，32（5）：681－687.

［5］ TSUMAK Y，NARUSE H，NENCHEV D N.Design of a compact 6－DOF haptic interface［Z］.Proceedings of the 1998 IEEE International Conference on Robotics＆Automation，Leuven，1998.

［6］ 刘善增，余跃庆，侣国宁，等.3自由度并联机器人的运动学与动力学分析［J］.机械工程学报，2009，45（8）：11－17.LIU Shanzeng，YU Yueqing，SI Guoning，et al.Kinematic and dynamic analysis of a three－degree－of－freedom parallel manipulator［J］.Journal of Mechanical Engineering，2009，45（8）：11－17.

［7］ 杨蒲，李奇.三轴陀螺稳定平台控制系统设计与实现［J］.中国惯性技术学报，2007，15（2）：171－176.YANG Pu，LI Qi.Design and realization of control system for three－axis gyro stabilized platform［J］.Journal of Chinese Inertial Technology，2007，15（2）：171－176.

［8］ 查峰，许江宁，黄寨华，等.单轴旋转惯导系统旋转性误差分析及补偿［J］.中国惯性技术学报，2012，20（1）：11－17.ZHA Feng，XU Jiangning，HUANG Zhaihua，et al.Analysis and compensation for rotary errors of INS with single axis rotation［J］.Journal of Chinese Inertial Technology，2012，20（1）：11－17.

［9］ HUANG MingZ，LING Shouhung，SHENG Yang.A study of velocity kinematics for hybrid manipulators with parallelseries configurations［Z］.Proceedings of 1993IEEE International Conference on Robotics and Automation，Atlanta：1993.

［10］ ALON Wolf，MOSHE Shoham.Screw theory tools for the synthesis of the geometry of a parallel robot for a given instantaneous task［J］.Mechanism and Machine Theory，2006，41（5）：656－670.