随机算子存在随机不动点的充分条件
2013-07-24赵金辉
赵金辉
(曲阜师范大学 图书馆,山东 曲阜 273165)
随机算子存在随机不动点的充分条件
赵金辉
(曲阜师范大学 图书馆,山东 曲阜 273165)
本文利用随机拓扑度理论研究随机凝聚算子,在某些边界条件下得到随机凝聚算子的随机不动点存在性.作为特例,得到确定性凝聚算子的不动点,减弱了已知文献中相关定理的条件.
随机凝聚算子;随机拓扑度;随机不动点
1 引言与主要结果
随机不动点问题是随机泛函分析的重要研究方向,而随机拓扑度是研究随机不动点问题的基本方法.关于随机不动点的存在性近期有很多研究,见[1-5]及其参考文献.因为随机凝聚算子包含了随机全连续算子为其特殊情形,所以本文仅对于随机凝聚算子给出存在随机不动点的充分条件.作为特例,得到相应边界条件下的确定性算子不动点定理,这个特例是已知文献结果的改进.
定理1.1 关于确定性凝聚算子的推论2.1减弱了[6]中主要定理的条件.已知文献中有关边界值条件下算子不动点问题,多数都是假定其范数的指数α≥1或者α>1,文献[2]中定理4、定理5是边界条件中范数指数α∈(0,1)的情况,本文定理1.2中假定α∈(0,1)本文内容丰富了随机算子不动点的内容.
假定 (Ω,Σ,μ)为完全的概率测度空间,(E,||·||)为可分Banach空间(即Polish空间),(E,B)为可测空间,其中B为E的一切Borel子集的σ-代数.称映象x∶Ω→E为E-值随机变量,若对任意S∈B,集合{ω∈Ω|x(ω)∈S}∈Σ.算子A∶Ω× E→E称为随机算子,若对任意的x∈E,A(ω,x)为E-值随机变量.
定义1.1 设A∶Ω×E→E是随机凝聚算子,f=I-A,对几乎所有的ω∈Ω,p∈Ef(ω,∂D)满足τ(ω)=d(p,f(ω,∂D))=infx∈∂D||f (ω,x)-p||>0,则对于几乎所有的ω∈Ω,degLS(f(ω,·),D,p)有意义,用下列概整值函数定义随机凝聚算子的随机拓扑度:
DegR(f(ω,x),D,p)=degLS(f(ω,x))|Ω0,a,s,on,Ω.
其中Ω0={ω|A(ω,·)是凝聚算子,p∈Ef(ω,∂D)},μ(Ω0)=1,f (ω,x)|Ω0表示f(ω,x)在Ω0上的限制.
随机拓扑度DegR(f(ω,x),D,p)具有L--S拓扑度的基本性质,如正规性、同伦不变性、可解性、边界值性质等.参见文献[7,8].
下述两个定理是本文的主要结果.
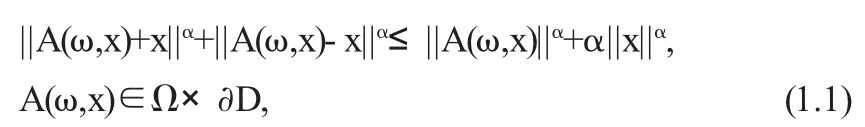
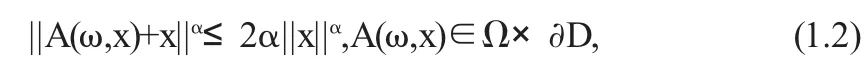
2 定理1.1的证明与推论
不妨设A(ω,x)在∂D上没有不动点,否则结论已成立.我们令

下面证明
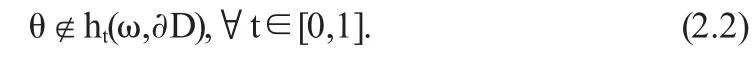
由θ∈D知道

由A(ω,x)在∂D上没有不动点知道

假若存在t0∈(0,1),x0∈∂D使得ht0(ω0,x0)=θ,可以写成为,将此式代入(1.1)式得到

这等价于


下面我们证明(2.5)式是不可能的.我们令


考察函数

由于
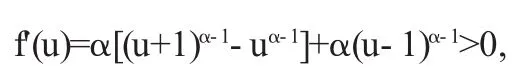
f(u)在[1,+∞)上为单调递增函数.又由(2.6)与(2.7)知道f (1)=2α-α-1>0,故当u≥1时,f(u)≥f(1)>0,于是有不等式

由于t0∈(0,1)于是(2.5)式与(2.8)式矛盾,此矛盾说明(2.5)是不可能的.由此知道
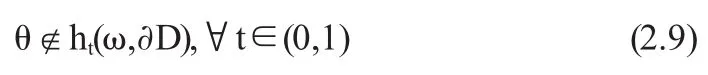
综合(2.3)(2.4)(2.9)知道(2.2)成立.从而由(2.1)与随机拓扑度的同伦不变性、正规性知道
当定理1.1中的算子A为确定性算子时,相应的结论仍成立,即为下述的推论.
推论2.1 设D⊂E是有界开集,θ∈D,A∶Ω×D→E是凝聚算子,且满足下式:

注1 条件(2.10)减弱了[6]中定理1的条件b),于是推论2.1减弱了[6]中主要定理的条件.
3 定理2.1的证明与推论
不妨设A(ω,x)在∂D上没有不动点,否则结论已成立.我们令

下面证明

类似于定理1.1的证明得到

假若存在t0∈(0,1),x0∈∂D使得ht0(ω0,x0)=θ,可以写成为,将此式代入(1.2)式得到

这等价于


下面我们证明(3.4)式是不可能的.我们令


综合(3.3)(3.5)知道(3.2)成立.容易验证同伦不变性的其它条件满足,从而由(3.1)及同伦不变性、正规性知道

于是由可解性知道A(ω,x)在D内必有随机不动点.
当α=1时,由定理1.2我们得到下述便于使用的推论.

推论3.2 设D⊂E是有界开集,θ∈D,A∶Ω×D→E是随机凝聚算子,且满足下式

注2 推论3.2是著名的Rethe不动点定理的随机形式.
〔1〕王梓坤.随机泛函分析引论.数学进展,1962(5):45-47.
〔2〕李国桢,许绍元.关于随机非线性算子的若干定理,数学进展,2006,35(6):721-729.
〔3〕李兴昌,赵增勤.一类随机减算子随机不动点存在唯一性定理及应用.数学物理学报,2012,32A(2):373-378.
〔4〕朱传喜.随机算子的若干新结果.应用数学,2002,15(4):34-37.
〔5〕张国娟,刘颖范.全连续随机算子的边界不动点定理,应用数学,2012,25(4):760-763.
〔6〕张国娟,刘颖范,施庆生.非自包含不动点定理及其在投入产出方程中的应用.应用数学学报,2010,33(3):509-513.
〔7〕Li Guozhen,Chen Yuching,On random topological degree and some random fixed point theorems,数学物理学报,1993,13(4):391-398.
〔8〕卢同善.随机泛函分析及其应用.青岛海洋大学出版社,1990.
O177.91
A
1673-260X(2013)11-0001-02
山东省自然科学基金资助项目(ZR 2012AQ 024,ZR 2012AM 006)
