基于ARIMA模型的CPI实证分析及预测

李 璇，黄冬冬

（1.深圳大学 中国经济特区研究中心，广东 深圳 518060；2.商丘工学院 管理学院，河南 商丘 476100）

一、现有研究成果

居民消费价格指数（Consumer Price Index，CPI），是一个反映居民家庭所购买的生活消费品和服务价格水平变动情况的宏观经济指标。它不仅影响政府制定货币、财政和社会保障等政策，也直接影响居民的生活水平［1］。同时，CPI也是反映通货膨胀的重要指标。一般说来，当CPI的增幅高于3%时，我们称为通货膨胀；而当CPI的增幅高于5%时，则称为严重的通货膨胀［2］。如果CPI增幅过大，表明通胀已经相当严重，会导致社会运行成本的增加和经济效率的降低，并影响社会收入分配。

CPI一直是国内外经济专家、学者研究的热点。世界银行、国际货币基金组织和英国共识公司等都曾对世界主要国家的CPI进行预测［3］。对CPI的准确预测有助于把握未来经济发展和人民生活状况，从而更能有效制定政策，对国民经济进行调控。我国学者在对CPI的年度和月度数据进行分析和预测方面的研究成果颇为丰富。如叶阿忠、李子奈利用我国1994年4月至1998年11月的CPI数据建立了混合回归和时间序列模型［4］。谢佳利、杨善朝、梁鑫运用时间序列的几个不同模型，对我国2001年1月至2007年8月的CPI变化规律进行比较分析，建立了一个反映CPI变化规律的较优统计预测模型，该模型的相对误差控制在1%之内，得到较好的结果［5］。李庆华运用VAR 模型对我国1990—2004年的CPI及其相关重要宏观经济数据进行回归分析，得出几点结论与建议［6］。陈娟、余灼萍运用Eviews 4.1软件和时间序列模型，分析我国1951—2002年的CPI统计资料，并进行相关预测，提出了几点看法和建议［7］。袁少华、熊正丰等分析了我国1990—2006 年的城市年度CPI 数据，并在ARIMA 模型方法和Eviews 5.0 软件的基础上建立广东省的CPI有效预测模型［8］。郑艳伟、钱乐祥等建立基于BP神经网络的CPI预测数学模型，利用该模型对广州的CPI进行预测，结果表明该模型的预测值与实测值的误差仅为0.91［9］。

本文利用时间序列分析中的ARIMA 模型对中国2000年1月至2012年12月期间的CPI月度数据进行建模分析，并预测2013 年CPI的走势。为市场预测与政府宏观经济政策的制定提供参考依据。

二、实证分析

1.ARIMA模型的建模思想

ARIMA（Autoregressive Integrated Moving Average）模型全称为差分自回归移动平均模型，是由Box和Jenkins于20世纪70年代初提出的一种著名时间序列预测方法。它是从时间序列自身出发，建立相应的模型进行分析，得出关于其过去行为的有关结论，并对其未来行为进行预测和推断。用这种方法预测时，不必考虑其他影响因素对其产生的影响，这样避免了寻找主要因素及识别主要因素和次要因素的困难。与回归分析方法相比，消除了模型中对随机扰动项的限定条件在经济实践中难以满足的矛盾［10］。由于其理论分析的深入彻底和应用分析的简单、有效，是线性时间序列预测的主要工具之一。

ARIMA（p，d，q）模型由3部分组成：自回归过程（AR（p）），AR 是自回归，即一个时间序列的当前值可以表示为滞后p 期观测值的线性组合；单整（I（d）），d 为时间序列成为平稳时所做的差分次数，指将一个非平稳时间序列，经过d 次差分后，转化为平稳序列①差分的原理是：某些时间序列是依赖于时间t的一组随机变量，构成该序列的单个序列值，虽然具有不确定性，但整个序列的变化却具有一定的规律性，可以用相应的数学模型近似描述。；移动平均过程（MA（q）），MA 为移动平均，即模型值可以表示为q阶残差项的线性函数。该模型的表达式如下：

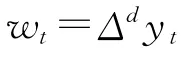
2.数据来源及分析

本文数据来源于中经网数据库、清华大学金融研究数据库和东方财富网，用我国2000年1月至2012年12 月的CPI月度数据作为研究的对象，数据如表1所示。

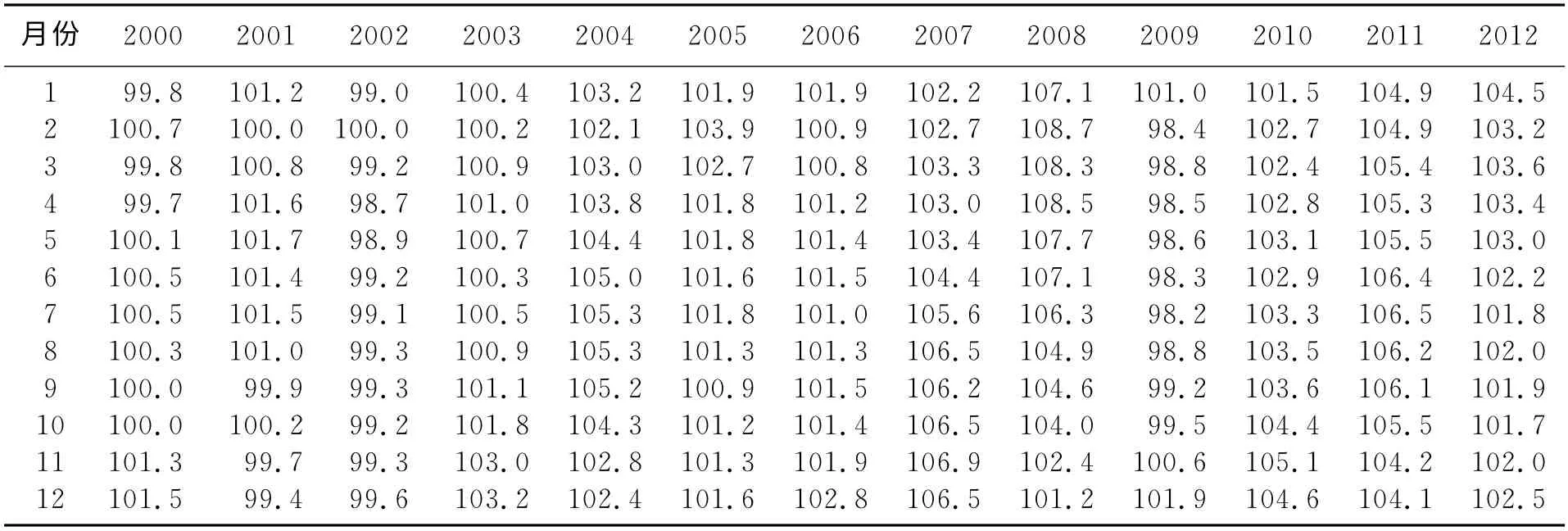
表1 2000—2012年中国居民CPI

对表1中的数据进行分析，从CPI的线状图（如图1）来判断回归模型的形式，由图1可以看出CPI波动比较大，但没有明显的趋势。因此，可利用包含截距项但不包含趋势项的ADF检验对CPI进行平稳性检验。

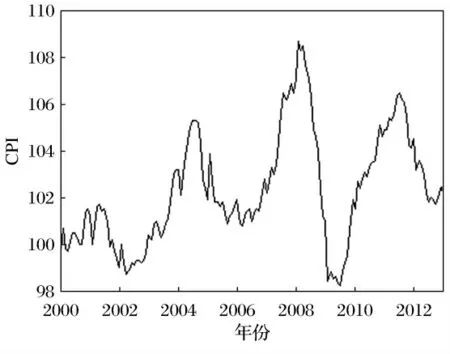
图1 2000—2012年中国居民CPI走势

3.平稳性检验及处理

运用Eviews 5.0对其进行单位根检验（如表2），可得ADF检验统计量的值等于－3.315 5，大于在1%和5%的检验水平下t统计量的临界值－4.021 2和－3.440 1，可以认为CPI至少有1个单位根，即该序列是不平稳的。

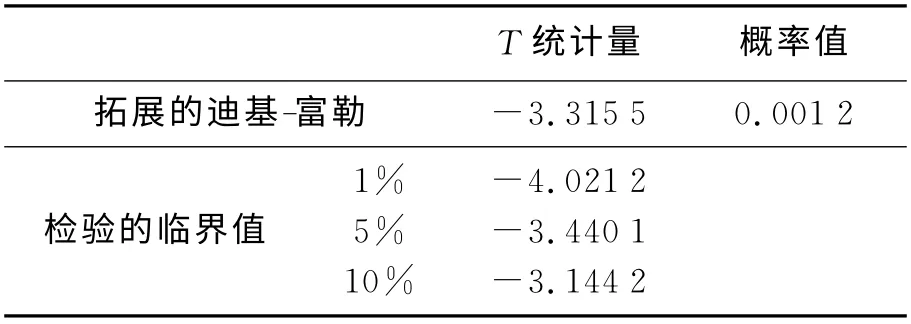
表2 CPI时间序列的单位根检验（ADF检验）

由表2可知CPI序列没有通过ADF检验即该时间序列是非不稳的。因此需要对序列CPI进行平稳化处理，在此运用差分法来消除序列的趋势。因此先对原始数据进行一阶差分，得到DCPI序列。DCPI序列ADF检验结果如表3所示。ADF检验的t统计量的值等于－3.982 2，小于在1% 的检验水平下t 统计量的临界值－3.474 9，所以DCPI在99%的置信区间内是平稳的。

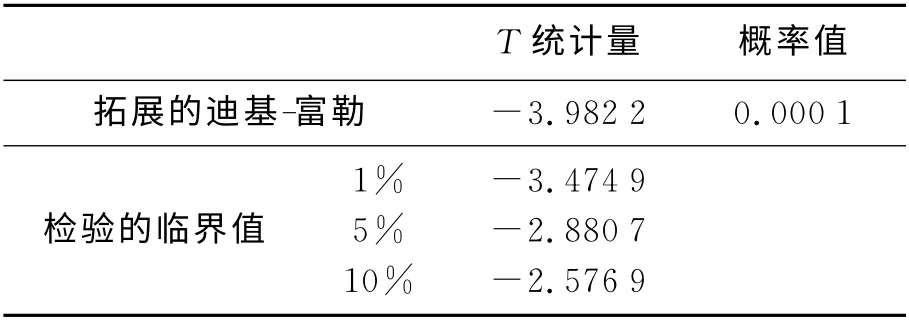
表3 DCPI时间序列的单位根检验（ADF检验）

4.模型识别及参数估计

找出适当的p、d 和q 值，运用ARIMA 模型最关键的工具是自相关图和偏自相关图。由平稳性检验可知CPI是一阶单整的，记I（1），即d＝1。为了找到合适的p 和q，对CPI的一阶差分变量DCPI进行自相关分析，图2给出了DCPI的自相关图和偏自相关图。

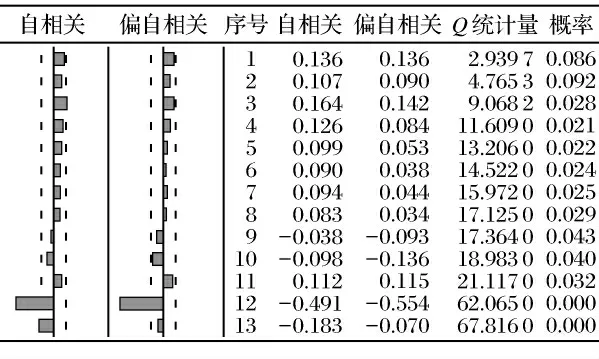
图2 DCPI的自相关图和偏自相关图

通过DCPI的自相关图和偏自相关图，可对CPI初步选择建立ARMIA（3，1，1）、ARIMA（3，1，2）和ARMIA（3，1，3）模型，再综合比较3个模型的AIC和SC值以及拟合程度来择优选择最佳模型进行分析和预测。

运用分析ARIMA（3，1，1）可知（见表4），模型AR 的3个倒数复根的模都小于1，说明所估计的ARIMA（3，1，1）模型是平稳的且可逆的。AIC值＝2.017 4，SC值＝2.116 9。

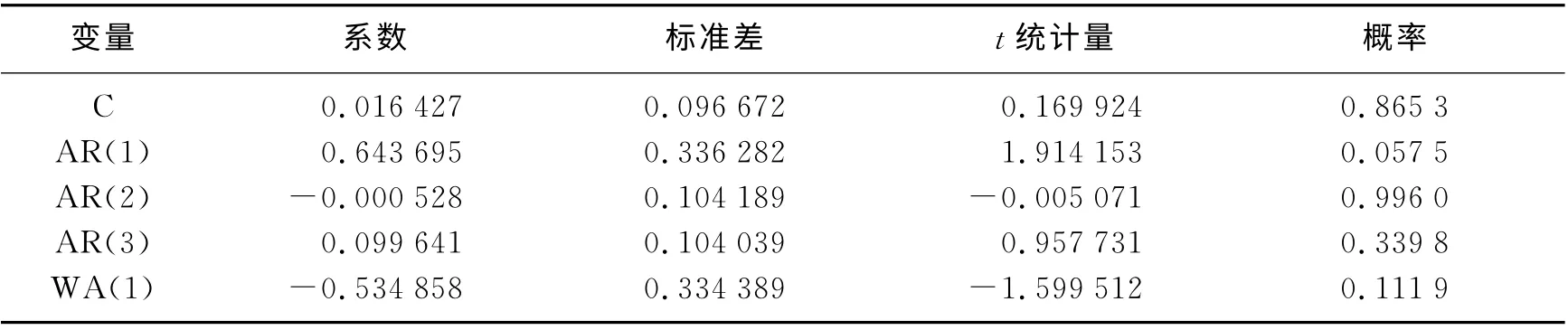
表4 ARIMA（3，1，1）模型结果

运用Eviews 5.0分析ARIMA（3，1，2）可知（见表5），模型AR 过程和MA 过程的复根都小于1，因此也可认为模型ARIMA（3，1，2）是平稳的且是可逆的。此模型中AIC 值＝2.026 4，SC＝2.145 8。

运用Eviews 5.0分析ARIMA（3，1，3）可知（见表6），模型AR 过程和MA 过程的复根都小于1，因此也可认为模型ARIMA（3，1，3）是平稳的且是可逆的。此模型中AIC 值＝1.926 9，SC值＝2.066 2。

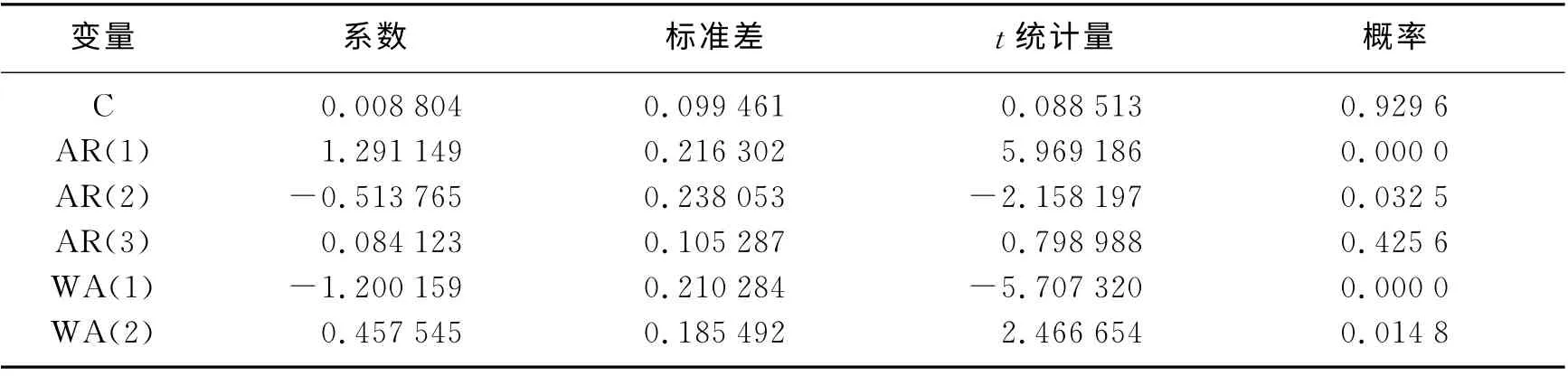
表5 ARIMA（3，1，2）模型结果

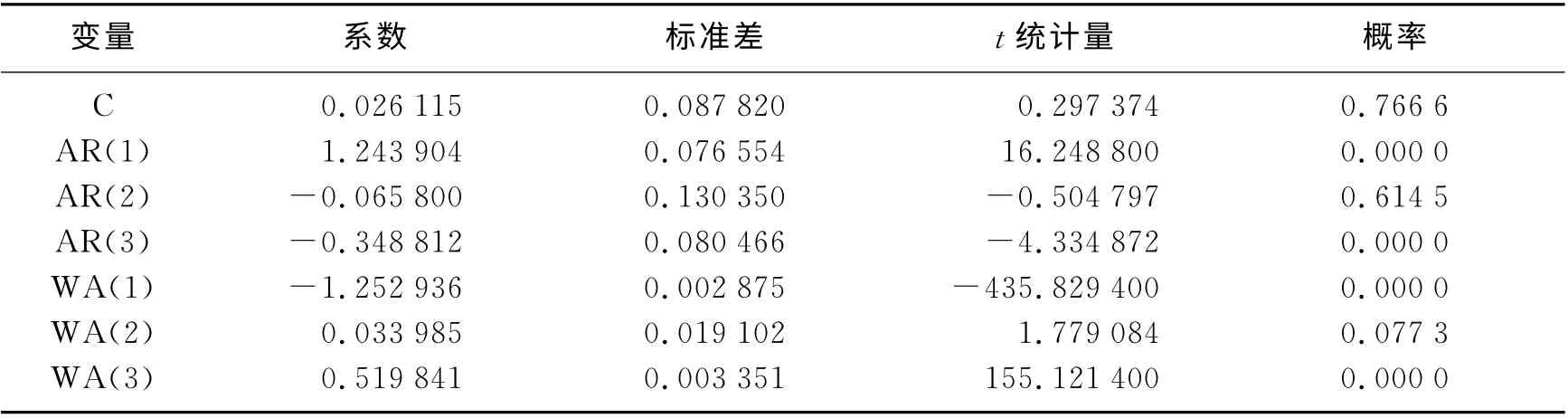
表6 ARIMA（3，1，3）模型结果

比较上述3种模型的AIC 值和SC 值可得，模型ARIMA（3，1，3）的AIC 值和SC 值都小于模型ARIMA（3，1，1）和ARIMA（3，1，2）的AIC和SC相应的值。根据AIC 值和SC 值最小化原则进行择优，可以认为模型ARIMA（3，1，3）比模型ARIMA（3，1，1）和ARIMA（3，1，2）更好。

而且从表6 的ARIMA（3，1，3）模型中可看出，AR 和MA 的2阶滞后项的系数检验不显著。因此，剔除这两项，得到修正后的ARIMA（3，1，3）模型（见表7），可利用滞后多项式写出修正后ARIMA（3，1，3）模型的估计结果。

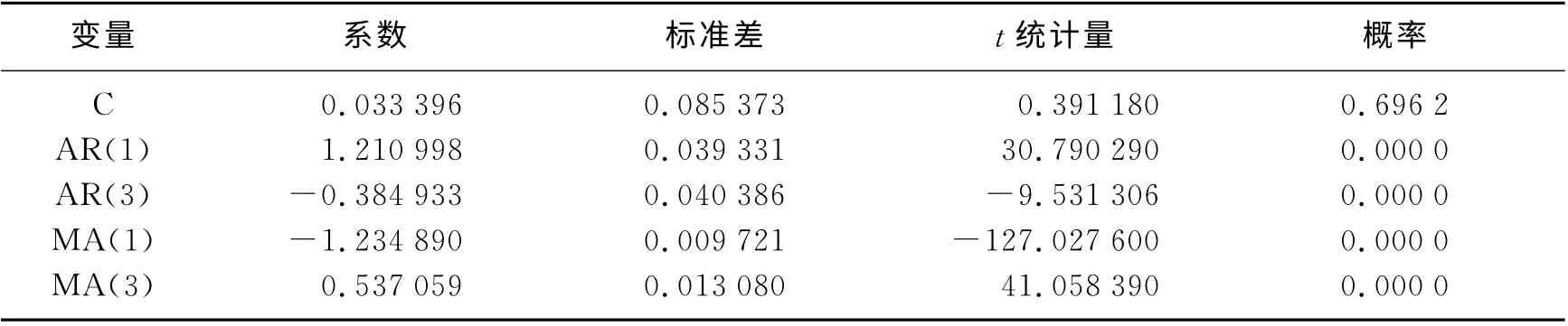
表7 修正后的ARIMA（3，1，3）模型结果

根据以上的修正结果，相应模型的表达式为

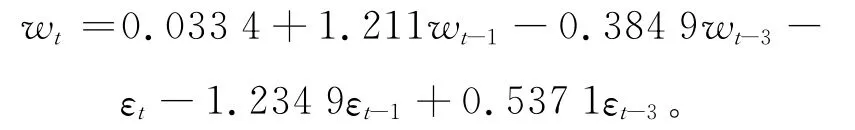
式中，F 统计量＝7.165 7，AIC 值＝1.902 6，SC值＝2.002 1。

5.模型检验

选定ARIMA（3，1，3）后诊断的目的是看所选的模型对数据拟合的是否够好。为了选取正确的ARIMA 模型，需要有高度的技巧。对所选模型的一个简单的检验，是看从该模型估计算出来的残差是不是白噪声。如果是，就可以接受这个拟合；如果不是则需进行修改，直到残差是白噪声为止。

残差序列的白噪声检验常用的是Q 统计量检验，检验的原假设是残差序列不存在自相关。残差序列的样本自相关函数为

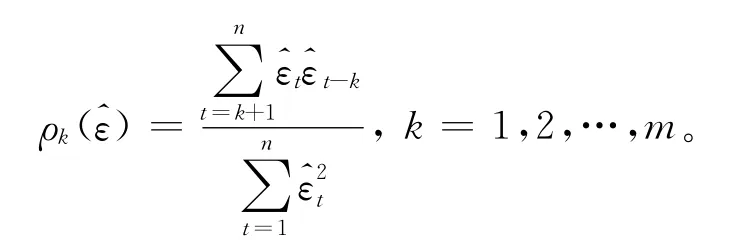
式中，n是计算的序列观测量。设m 是最大的滞后期数，由此构造检验统计量Q：

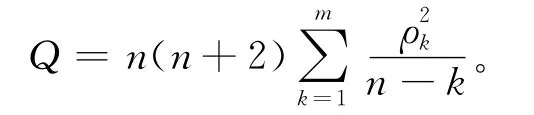
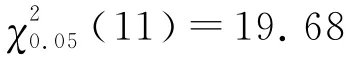
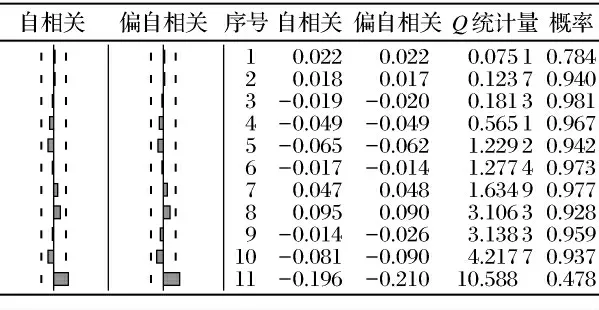
图3 白噪声检验结果

6.模型预测

以上的分析说明，建立的模型是合适的，因此可用其进行预测。通过Eviews 5.0 软件，得到2013年的CPI预测值（如表8）。

从已获得的数据中看到，我国的CPI在2013年上半年将一直上涨，但总的来说，涨幅是温和的。根据预测的结果，2013 年1—6 月我国CPI较2012 年同期分别增长－0.17%、1.12%、0.76%、0.99%、1.41%、2.24%。

表8 2013年1—6月CPI的预测值

三、结 语

由于有很多复杂的因素对CPI产生直接或间接的影响，利用这些因素建模并准确预测CPI是非常困难的。本文分析发现，综合反映全部因素的CPI本身是一组1 阶单整的时间序列，用ARIMA（p，d，q）为我国CPI预测构建模型比较合适。通过比较ARIMA（3，1，1），ARIMA（3，1，2）和ARIMA（3，1，3）模型的拟合效果，以及各模型的AIC、SC值，发现ARIMA（3，1，3）模型较好地拟合了我国过去的CPI数据，并可提供较好的预测。

［1］ 何书元.应用时间序列分析［M］.北京：北京大学出版社，2003：187－188.

［2］ 姜弘.居民消费价格指数的时间序列分析及预测［J］.统计与决策，2009（4）：117－118.

［3］ 赵云城.国际货币基金组织对世界及主要国家CPI预测［R］.世界经济运行报告，2011－2012.

［4］ 叶阿忠，李子奈.我国通货膨胀的GARCH 模型［J］.系统工程理论与实践，2000（10）：46－48.

［5］ 谢佳利，杨善朝，梁鑫.我国CPI时间序列预测模型的比较及实证检验［J］.统计与决策，2008（9）：4－6.

［6］ 李庆华.基于VAR 模型的中国消费价格指数分析［J］.华中师范大学学报：人文社会科学版，2006（4）：56－61.

［7］ 陈娟，余灼萍.我国居民消费价格指数的短期预测［J］.统计与决策，2005（4）：40－41.

［8］ 袁少华，熊正丰.我国城市年度CPI预测模型研究：以广东省为例［J］.消费导刊，2008（9）：28－29.

［9］ 郑艳伟，钱乐祥，张红光，等.利用神经网络对居民消费价格指数预测的研究：以广州为例［J］.云南地理环境研究，2006（11）：67－70.

［10］ 朱威，钟惟剑.ARMA 模型在居民消费价格指数预测中的应用［J］.金融经济，2008（8）：82－83.

［11］ 刘振威.基于ARIMA 模型对我国CPI未来走势的实证分析［J］.华北金融，2009（9）：10－11.

［12］ 翁东东.消费者价格指数的预测：基于ARIMA 模型的实证分析［J］.科技和产业，2010（6）：87－90.