基于小波域奇异值分解的振动信号压缩算法
2013-07-21王怀光张培林陈林陈彦龙
王怀光,张培林,陈林,陈彦龙
(1.军械工程学院 七系,石家庄,050003;2.武汉军械士官学校 枪械系,武汉,430075)
状态监测技术有助于改进系统可靠性、安全性并降低维护维修费用[1],在对设备的实时监测中将产生大量数据,必须对监测数据进行快速传输才能提高识别速度,满足在线测试的要求,因此必须研究相应的压缩方法。
矩阵的奇异值分解是矩阵论的重要内容,在在线动态系统识别、试验数据处理、最佳逼近问题及压缩算法等方面得到了广泛运用[2-5]。小波分解是一种常用的压缩算法[6-7],但小波分解后各层的小波系数不能直接运用矩阵分析。为有效运用矩阵方法分析小波系数,提取小波系数中的本质信息,提出了一种基于小波域奇异值分解的轴承振动信号压缩算法。首先,将工程采集的时间序列进行小波变换;然后,经过数学处理,从一维变换为二维构造矩阵;最后,利用奇异值分解提取出反映轴承振动信号本质特征的奇异值和奇异值向量,完成信号的压缩。
1 小波系数二维矩阵的构建
小波分解结构如图1所示。经小波分解后,同层间小波系数的个数相等,而上一层小波系数的个数为下一层的2倍,无法将不同层次的小波系数直接用于构建矩阵。

图1 小波分解结构
为解决这个问题,提出将小波系数进行补零处理。假设第1层小波系数长度为n,则第m层小波系数的个数为n/2m-1,将第m层小波系数进行补零处理,则新生成的第m层的小波系数为

j=1,2,…,n。
其中,coefm(j)(j=1,2,…,n/2m-1)为小波分解后第m层的原始小波系数,运用新构建的小波系数组成矩阵为
式中:new_cd_coefm(i)为根据第m层原始小波细节系数新生成的小波细节系数;new_ca_coefm(i)为根据第m层原始小波近似系数新生成的小波近似系数。
2 基于奇异值分解的信号压缩方法
2.1 矩阵的奇异值分解理论
对于矩阵A∈Cm×n,存在m阶酉矩阵U∈Cm×m和n阶酉矩阵V∈Cn×n使得[8]
A=USVH,
(1)
式中:S为A的奇异值矩阵;σ1,σ2…,σr为A的奇异值;对角元素满足σ1≥σ2≥…≥σr>0,r=rank(A)。
将矩阵U和V用列向量表示为
U=[u1,u2,…,um],
(2)
V=[v1,v2,…,vn]。
(3)
ui为σi对应的左奇异向量,vi为σi对应的右奇异向量,矩阵A可进一步表达为
(4)
上式为向量积的线性组合,称为矩阵A的奇异值展开式。
2.2 基于奇异值分解的压缩算法
根据(4)式,按从大到小的原则选取k个奇异值与相应的左、右奇异向量重构矩阵A,表示为
(5)
如果k≥r,可完整恢复信号,讨论k (6) 奇异值的累积贡献度定义为 (7) 数据的压缩比定义为 (8) 根据ρ值,可以确定用于重构信号的奇异值数目k,原始矩阵A需要m×n个数据表示,Ak则使用k(m+n+1)个数据表示。在k(m+n+1)个数据中,k×m,k×n分别表示矩阵U,V前k列元素的数据总量;k×1表示矩阵A的前k个奇异值。 ρ越小,用于表示Ak的数据量越小,压缩比越大,数据损伤则越严重;ρ越接近1,Ak包含A的主要信息越多,用于表示Ak的数据量越大,压缩比越小,数据损伤就越小;当ρ=1时,k≥r,Ak=A。研究表明,矩阵A的奇异值中只有小部分数值较大,其余均较小,因此较小的k(k 工程数据往往存在冗余,特别是旋转机械产生的周期信号。对矩阵进行奇异值分解后往往能够反映出矩阵的本质特征,减小数据间的相关性,可用于压缩振动信号。具体压缩过程为(图2): 图2 数据压缩流程 (1)将采集的时间序列信号s进行小波分解,并按照文中方法构成系数矩阵A∈Rm×n; (2)对小波系数矩阵A进行奇异值分解; (3)设定ρ值,并据此确定奇异值个数k; (4)选取前k个奇异值与对应的左、右奇异向量重构样本矩阵Ak; (5)将Ak中的m个n维向量依次拼接还原为时间序列s′。 安装于某齿轮箱的轴承型号为SKF6205-2RS,工作时承受径向载荷。采用电蚀在钢球上加工出直径为0.18 mm的单点故障,轴承的转速为1 796 r/min,以12 kHz的频率采集振动加速度信号,采用4 096个采样点进行分析。加速度传感器安装在驱动端,振动信号由16通道的DAT记录仪收集,前0.3 s的时域波形如图3所示。 图3 轴承钢球故障波形 小波压缩采用db1小波,7层分解。压缩比为CR=mn/k(m+n+1)。 压缩优劣评价的一个重要指标是数据还原程度,简单有效的评价方法是计算能量比(energy ratio,ER),即 (9) 式中:n为信号长度,s为原始信号,s′为重建信号。 压缩比不同时,小波域奇异值压缩和奇异值压缩所能达到的能量比见表1。压缩比相同时,小波域奇异值压缩所能达到的能量比更高,压缩效果更好。压缩比为2.656 3时,采用小波域奇异值压缩所得波形如图4所示,经压缩后的波形较好的保留了原始信号的特征。 表1 不同压缩比情况下的能量比 图4 小波域奇异值重构波形 为了验证文中算法的鲁棒性,有必要讨论信号长度对算法的影响。分解层数为7时,信号长度的影响如图5所示。由图可知,随着信号长度的变化,压缩比、能量比变化曲线形状相似,曲线对应的值接近,说明算法具有很强的鲁棒性。 图5 信号长度的影响 提出了基于小波域奇异值分解的振动信号压缩方法。通过补零,解决了小波系数不能直接构建矩阵的问题,将一维时间序列变换为二维小波系数矩阵,有助于引入矩阵分析方法,借助奇异值分析系数矩阵,从而提取小波系数的本质特征。 将文中方法应用于压缩轴承钢球的故障信号,获得的压缩比较高,且在相同的压缩比下,该方法比奇异值压缩信号获得的能量比更高。与其他方法相比,该方法运算速度快,理论实现简单,是一种简单快速的信号压缩方法。2.3 轴承振动信号的奇异值分解压缩

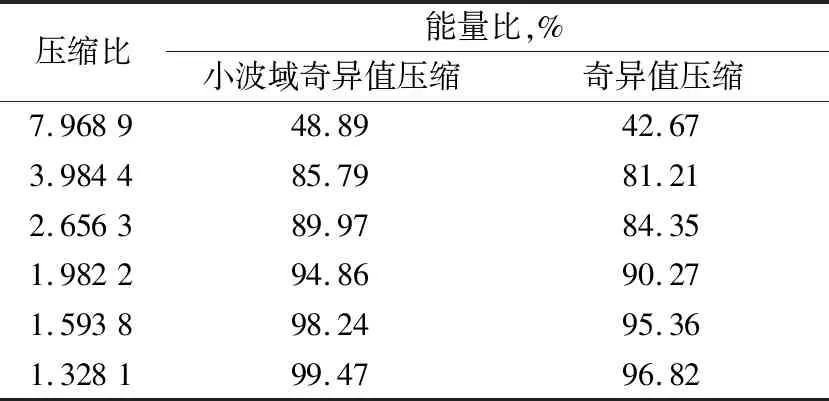
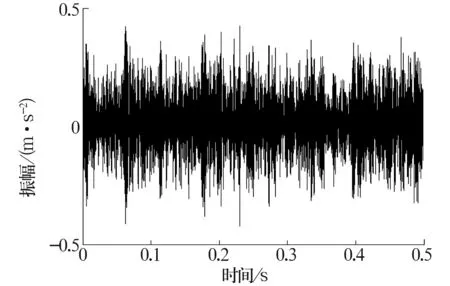
3 轴承信号压缩


4 结束语
